Frontiers in Genetics
Introduction
La taille effective de la population (Ne) est un paramètre génétique important qui estime la quantité de dérive génétique dans une population, et a été décrite comme la taille d’une population de Wright-Fisher idéalisée qui devrait donner la même valeur d’un paramètre génétique donné que dans la population à l’étude (Crow et Kimura, 1970). La taille des Ne peut être influencée par les fluctuations de la taille de la population de recensement (Nc), par le sex-ratio de reproduction et par la variance du succès reproducteur.
L’estimation Ne peut être réalisée à l’aide d’approches qui relèvent de trois catégories méthodologiques : démographiques, basées sur le pedigree ou basées sur des marqueurs (Flury et al., 2010). Les données généalogiques ont été traditionnellement utilisées pour obtenir des estimations de Ne chez le bétail. Cependant, les estimations fiables de Ne dépendent de l’exhaustivité du pedigree. Cet état des connaissances est réalisable dans certaines populations domestiques, dont les paramètres démographiques ont été suivis avec précision depuis un nombre suffisamment important de générations. Cependant, dans la pratique, l’applicabilité de cette approche reste limitée à quelques cas impliquant des races hautement gérées (Flury et al., 2010; Uimari et Tapio, 2011).
Une solution pour surmonter la limitation d’un pedigree incomplet consiste à estimer la tendance récente en Ne à l’aide de données génomiques. Plusieurs auteurs ont reconnu que Ne pouvait être estimé à partir d’informations sur le déséquilibre de liaison (LD) (Sved, 1971; Hill, 1981). LD décrit l’association non aléatoire d’allèles dans différents loci en fonction du taux de recombinaison entre les positions physiques des loci dans le génome. Cependant, les signatures LD peuvent également résulter de processus démographiques tels que le mélange et la dérive génétique (Wright, 1943; Wang, 2005), ou de processus tels que « l’auto-stop » lors de balayages sélectifs (Smith et Haigh, 1974) ou la sélection de fond (Charlesworth et al., 1997). Dans de tels scénarios, les allèles à différents loci deviennent associés indépendamment de leur proximité dans le génome. En supposant qu’une population est fermée et panmictique, la valeur de la DL calculée entre des loci neutres non liés dépend exclusivement de la dérive génétique (Sved, 1971; Hill, 1981). Cette occurrence peut être utilisée pour prédire Ne en raison de la relation connue entre la variance de LD (calculée à l’aide de fréquences d’allèles) et la taille effective de la population (Hill, 1981).
Progrès récents de la technologie du génotypage (p. ex., en utilisant des réseaux de billes SNP avec des dizaines de milliers de sondes d’ADN) ont permis la collecte de grandes quantités de données de liaison à l’échelle du génome, idéales pour estimer le Ne chez le bétail et les humains, entre autres (par exemple, Tenesa et al., 2007; de Roos et coll., 2008; Corbin et coll., 2010; Uimari et Tapio, 2011; Kijas et coll., 2012). Cependant, un outil logiciel permettant d’estimer le Ne à partir du LD fait défaut, et les chercheurs s’appuient actuellement sur une combinaison d’outils pour manipuler les données, déduire le LD et ont tendance à utiliser des scripts sur mesure pour effectuer les calculs appropriés et estimer le Ne.
Nous décrivons ici le SNeP, un outil logiciel qui permet d’estimer les tendances en Ne à travers la génération en utilisant des données SNP qui corrige la taille de l’échantillon, le phasage et le taux de recombinaison.
Matériaux et méthodes
La méthode utilisée par le SNeP pour calculer la DL dépend de la disponibilité des données par phases. Lorsque la phase est connue, l’utilisateur peut sélectionner le coefficient de corrélation au carré de Hill et Robertson (1968) qui utilise les fréquences d’haplotype pour définir LD entre chaque paire de loci (équation 1). Cependant, en l’absence d’une phase connue, le coefficient de corrélation produit-moment de Pearson au carré entre des paires de loci peut être sélectionné. Bien que ces deux approches ne soient pas les mêmes, elles sont très comparables (McEvoy et al., 2011):
où pA et pB sont respectivement les fréquences des allèles A et B à deux loci distincts (X, Y ) mesurée pour n individus, pAB est la fréquence de l’haplotype avec allèles A et B dans la population étudiée, X et Y sont les fréquences moyennes de génotype pour le premier et le deuxième locus respectivement, Xi est le génotype de l’individu i au premier locus et Yi est le génotype de l’individu i au deuxième locus. L’équation (2) met en corrélation le nombre d’allèles génotypiques au lieu des fréquences d’haplotype et n’est pas influencée par les hétérozygotes doubles (cette approche aboutit aux mêmes estimations que l’option –r2 dans PLINK).
Le SNeP estime la taille effective historique de la population sur la base de la relation entre r2, Ne et c (taux de recombinaison), (Équation 3-Sved, 1971), et permet aux utilisateurs d’inclure des corrections pour la taille de l’échantillon et l’incertitude de la phase gamétique (Équation 4 – Weir et Hill, 1980):
où n est le nombre d’individus échantillonnés, β = 2 lorsque la phase gamétique est connue et β = 1 si au contraire la phase n’est pas connue.
Plusieurs approximations sont utilisées pour déduire le taux de recombinaison en utilisant la distance physique (δ) entre deux loci comme référence et en la traduisant en distance de liaison (d), qui est généralement décrite comme Mb(δ) ≈ cM(d). Pour les petites valeurs de d, cette dernière approximation est valable, mais pour les grandes valeurs de d, la probabilité d’événements de recombinaison multiples et d’interférences augmente, de plus la relation entre la distance cartographique et le taux de recombinaison n’est pas linéaire, car le taux de recombinaison maximum possible est de 0,5. Ainsi, à moins d’utiliser δ très court, l’approximation d ≈ c n’est pas idéale (Corbin et al., 2012). Nous avons donc mis en œuvre des fonctions de cartographie pour traduire le d estimé en c, à la suite de Haldane (1919), Kosambi (1943), Sved (1971) et Sved et Feldman (1973). Initialement SNeP déduit d pour chaque paire de SNP comme directement proportionnel à δ selon d = kδ où k est une valeur de taux de recombinaison définie par l’utilisateur (la valeur par défaut est de 10-8 comme dans Mb = cM). La valeur déduite de δ peut alors être soumise à l’une des fonctions de mappage disponibles si l’utilisateur le souhaite.
La résolution de l’équation (3) pour Ne et incluant toutes les corrections décrites, permet la prédiction de Ne à partir des données LD en utilisant (Corbin et al., 2012):
où Nt est la taille effective de la population t il y a des générations calculée comme t =(2f(ct))-1 (Hayes et al., 2003), ct est le taux de recombinaison défini pour une distance physique spécifique entre marqueurs et éventuellement ajusté avec les fonctions de cartographie mentionnées ci-dessus, r2adj est la valeur LD ajustée pour la taille de l’échantillon et α: = {1, 2, 2.2} est une correction pour l’apparition de mutations (Ohta et Kimura, 1971). Par conséquent, la DL sur de plus grandes distances de recombinaison est informative sur les Ne récents, tandis que des distances plus courtes fournissent des informations sur des temps plus lointains dans le passé. Un système de binning est mis en œuvre afin d’obtenir des valeurs moyennes de r2 qui reflètent LD pour des distances inter-locus spécifiques. Le système de binning implémenté utilise la formule suivante pour définir les valeurs minimales et maximales pour chaque bin:
Où bi(ℕ1) est le i bac du nombre total de bacs (totBins), minD et maxD sont respectivement le minimum et le la distance maximale entre SNPs et x est un nombre réel positif (ℝ0) Lorsque x est égal à 1, la distribution des distances entre les bacs est linéaire et chaque bac a la même plage de distances. Pour des valeurs de x plus grandes, la distribution des distances change, ce qui permet une plage plus grande sur les derniers bacs et une plage plus petite sur les premiers bacs. La variation de ce paramètre permet à l’utilisateur d’avoir un nombre suffisant de comparaisons par paires pour contribuer à l’estimation Ne finale pour chaque bac.
Exemple d’application
Nous avons testé le SNeP avec deux jeux de données publiés qui avaient déjà été utilisés pour décrire les tendances de Ne au fil du temps en utilisant LD, Bos indicus et Ovis aries. Les estimations r2 pour les ensembles de données sur les bovins ont été obtenues par les auteurs à l’aide de GenABLE (Aulchenko et al., 2007) en utilisant une fréquence d’allèle minimale (CRG) < 0,01 et en ajustant le taux de recombinaison à l’aide de la fonction de cartographie de Haldane (Haldane, 1919). Les estimations r2 des données sur les moutons ont été calculées par les auteurs à l’aide de PLINK-1.07 (Purcell et al., 2007), avec un CRG < 0,05 et aucune autre correction. Pour les deux ensembles de données autosomiques, les estimations r2 ont été corrigées en fonction de la taille de l’échantillon à l’aide de l’équation (4) avec β = 2. Pour ces analyses comparatives, la ligne de commande du SNeP incluait les mêmes paramètres utilisés pour les données publiées, à l’exception des estimations r2, calculées grâce au nombre de génotypes et à l’utilisation de la nouvelle stratégie de binning du SNeP.
Résultats
SNeP est une application multithread développée en C++ et les binaires pour les systèmes d’exploitation les plus courants (Windows, OSX et Linux) peuvent être téléchargés à partir de https://sourceforge.net/projects/snepnetrends/. Les binaires sont accompagnés d’un manuel décrivant l’utilisation étape par étape de SNeP pour déduire les tendances en Ne comme décrit ici. SNeP produit un fichier de sortie avec des colonnes délimitées par des tabulations montrant ce qui suit pour chaque bac qui a été utilisé pour estimer Ne : le nombre de générations dans le passé auxquelles le bac correspond (par ex., il y a 50 générations), l’estimation Ne correspondante, la distance moyenne entre chaque paire de SNP dans le bac, la moyenne r2 et l’écart type de r2 dans le bac, et le nombre de SNP utilisés pour calculer r2 dans le bac. Ce fichier peut être facilement importé dans Microsoft Excel, R ou un autre logiciel pour tracer les résultats. Les graphiques présentés ici (Figures 1, 3) correspondent aux colonnes d’il y a des générations et Ne du fichier de sortie. La colonne avec l’écart-type r2 est fournie aux utilisateurs pour inspecter la variance de l’estimation Ne dans chaque bac, en particulier pour les bacs reflétant des estimations temporelles plus anciennes et qui sont moins fiables à mesure que le nombre de SNP utilisés pour estimer r2 devient plus petit.
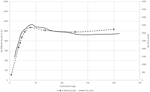
Figure 1. Comparaison des tendances en Ne de six races ovines suisses selon Burren et al. (2014) (lignes pointillées) et ce travail (lignes continues).
Le format requis pour les fichiers d’entrée est le format PLINK standard (fichiers ped et map) (Purcell et al., 2007). SNeP permet aux utilisateurs de calculer LD sur les données comme décrit ci-dessus, ou d’utiliser une matrice LD précalculée personnalisée pour estimer Ne à l’aide de l’équation (5).
L’interface logicielle permet à l’utilisateur de contrôler tous les paramètres de l’analyse, par exemple la plage de distance entre les SNP en bp et l’ensemble des chromosomes utilisés dans l’analyse (par exemple, 20-23). De plus, SNeP inclut la possibilité de choisir un seuil de CRG (0 par défaut.05), car il a été démontré que la prise en compte du CRG donne lieu à des estimations r2 impartiales, quelle que soit la taille de l’échantillon (Sved et al., 2008). L’architecture multithread du SNeP permet un calcul rapide de grands ensembles de données (nous avons testé jusqu’à ~ 100K SNPs pour un seul chromosome), par exemple les données BOS décrites ici ont été analysées avec un processeur en 2’43 », l’utilisation de deux processeurs a réduit le temps à 1’43 », quatre processeurs ont réduit le temps d’analyse à 1’05 ».
Exemple de zébu
Pour l’analyse du zébu, les formes des courbes Ne obtenues avec le SNeP et les tendances de leurs données publiées ont montré la même trajectoire avec une baisse en douceur jusqu’à il y a environ 150 générations, suivie d’une expansion avec un pic il y a environ 40 générations et se terminant par une forte baisse sur les générations les plus récentes (Figure 1). Cependant, alors que les tendances des deux courbes étaient les mêmes, les deux approches ont abouti à des estimations Ne différentes, les valeurs du SNeP étant environ trois fois plus grandes que celles de l’article original. Alors que nous avons tenté d’utiliser les paramètres des auteurs dans nos analyses, certaines différences étaient inévitables, c’est-à-dire la publication originale des données sur les bovins estimées r2 avec une approche différente de celle mise en œuvre dans le SNeP. Les analyses avec le SNeP étaient basées sur des génotypes, tandis que l’analyse initiale était basée sur deux haplotypes de locus déduits, ce qui a donné aux données publiées un r2 attendu de 0,32 à la distance minimale, alors que nos estimations étaient de 0,23. De même, Mbole-Kariuki et al. (2014) ont obtenu un niveau de fond r2 = 0,013 autour de 2 Mo, alors que notre estimation à la même distance était de 0.0035 (données non représentées). Par conséquent, comme nos estimations de la DL étaient constamment inférieures à celles de Mbole-Kariuki et al. (2014) on s’attend à ce que nos estimations Ne soient plus importantes. Si cette observation souligne l’importance d’un choix minutieux des paramètres et de leurs seuils, il est important de souligner que bien que l’amplitude absolue des valeurs Ne soit différente, les tendances sont presque identiques.
Exemple de moutons suisses
Les six races de moutons suisses analysées avec le SNeP ont produit des résultats comparables à ceux de l’article original (Figure 2), avec des courbes de tendance Ne se chevauchant pour la plupart (Figure 3). Cependant, la tendance générale en Ne a montré un déclin vers le présent. Le SNeP a produit des valeurs légèrement plus grandes de Ne pour le passé plus lointain (700-800 générations). Cela est dû au système de binning différent utilisé dans SNeP, qui permet à l’utilisateur d’obtenir une distribution plus uniforme des comparaisons par paires dans chaque bin (i.e., le nombre de comparaisons par paires de SNP dans chaque bac est comparable). Pour la période allant au-delà d’il y a 400 générations, Burren et al. (2014) n’ont utilisé que trois bacs dans leur analyse (centrés sur les générations 400, 667 et 2000) tandis que pour la même période, le SNeP a utilisé 5 bacs avec un nombre de comparaisons par paires dépendant de la plage définie avec les formules 6a, b. Par conséquent, l’approche de Burren et ses collègues se termine par une densité plus élevée de données décrivant les générations les plus récentes que décrivant les générations les plus anciennes. Par conséquent, l’utilisation de moins de bacs tend à augmenter la présence de plus petites valeurs de Ne dans chaque bac, abaissant par conséquent la valeur moyenne de Ne pour chaque bac. Les valeurs de Ne pour le passé récent, comparées à la 29e génération dans le passé, ont donné des résultats très similaires. La plus grande différence (50) a été obtenue pour la race SBS.

Figure 2. Comparaison entre les valeurs Ne récentes calculées à la 29e génération dans ce travail et Burren et al. (2014) pour six races ovines suisses.
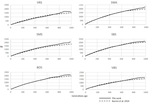
Figure 3. Comparaison des tendances Ne pour les 250 dernières générations dans les données SHZ obtenues par Mbole-Kariuki et al. (2014) (ligne pointillée) et en utilisant SNeP (ligne continue).
Discussion
L’analyse de Ne à l’aide de données sur la DL a été démontrée pour la première fois il y a 40 ans et a été appliquée, développée et améliorée depuis (Sved, 1971; Hayes et al., 2003; Tenesa et coll., 2007; de Roos et coll., 2008; Corbin et coll., 2012; Sved et coll., 2013). Le nombre traditionnellement faible de SNP analysés n’est plus une limitation, car les puces SNP comprennent un nombre extrêmement important de SNP, disponibles en peu de temps et à un prix raisonnable. Cela a stimulé l’utilisation de la méthode, qui a été appliquée à l’homme (Tenesa et al., 2007; McEvoy et coll., 2011) ainsi qu’à plusieurs espèces domestiquées (England et al., 2006; Uimari et Tapio, 2011; Corbin et coll., 2012; Kijas et coll., 2012). Parallèlement à ces améliorations, des limites méthodologiques sont devenues apparentes et ont été abordées ici, la majorité des efforts visant à estimer correctement les Ne récents. Pourtant, la valeur quantitative de l’estimation dépend fortement de la taille de l’échantillon, du type d’estimation de la DL et du processus de regroupement (Waples et Do, 2008; Corbin et al., 2012), alors que son modèle qualitatif dépend davantage de l’information génétique que de la manipulation des données.
Jusqu’à présent, cette méthode a été appliquée à l’aide de divers logiciels, il n’existe aucune approche standardisée pour regrouper les résultats et chaque étude a appliqué une approche plus ou moins arbitraire, par exemple le regroupement des classes de génération dans le passé (Corbin et al., 2012), binning pour les classes de distance avec une plage constante pour chaque bin (Kijas et al., 2012) ou des classes de binning par distance de manière linéaire, mais avec des bacs plus grands pour les points temporels les plus récents (Burren et al., 2014). À notre connaissance, le seul logiciel disponible qui estime Ne par LD est NeEstimator (Do et al., 2014), une version améliorée de l’ancien LDNE (Waples et Do, 2008) permettant l’analyse de grands ensembles de données (comme 50k SNPChip). Fait important, alors que le SNeP se concentre sur l’estimation des tendances historiques en Ne, l’objectif de NeEstimator est de produire des estimations contemporaines impartiales en Ne, ces dernières doivent donc être considérées comme un outil complémentaire lors de l’étude de la démographie par LD.
Nous avons utilisé le SNeP pour analyser deux ensembles de données où la méthode était précédemment appliquée. Les résultats que nous avons obtenus pour les données sur les moutons étaient à la fois quantitativement et qualitativement comparables à ceux obtenus par Burren et al. (2014), tandis que pour les données sur le zébu, nous avons obtenu une estimation de la tendance Ne qui correspondait étroitement à celle de Mbole-Kariuki et al. (2014) bien que nos estimations ponctuelles de Ne soient plus grandes que celles décrites pour les données (Mbole-Kariuki et al., 2014). L’écart entre ces deux résultats reflète que Burren et ses collègues ont produit leurs estimations r2 en utilisant PLINK (le logiciel standard pour la manipulation de données SNP à grande échelle) qui utilise la même approche utilisée pour estimer r2 par SNeP, tandis que Mbole-Kariuki et al. suivi de Hao et coll. (2007) pour l’estimation r2. L’utilisation de différentes estimations pour LD est critique pour l’aspect quantitatif de la courbe Ne, où en raison de la corrélation hyperbolique entre Ne et r2, une diminution de r2 sur sa plage plus proche de 0 peut entraîner une très grande variation des estimations Ne, tandis que les différences d’estimations sont moins significatives lorsque la valeur de r2 est élevée, c’est-à-dire plus proche de 1. Par conséquent, bien que dans l’un des ensembles de données, les valeurs Ne soient sensiblement différentes, dans les deux cas, les courbes Ne se chevauchent avec celles publiées à l’origine.
Comme l’ont déjà suggéré d’autres auteurs, la fiabilité des estimations quantitatives obtenues avec cette méthode doit être prise avec prudence, en particulier pour les valeurs Ne liées aux générations les plus récentes et les plus anciennes (Corbin et al., 2012) parce que pour les générations récentes, de grandes valeurs de c sont impliquées, ne correspondent pas aux implications théoriques proposées par Hayes pour estimer une variable Ne au fil du temps (Hayes et al., 2003). Les estimations pour les générations les plus anciennes pourraient également être peu fiables car la théorie coalescente montre qu’aucun SNP ne peut être échantillonné de manière fiable après 4Ne générations dans le passé (Corbin et al., 2012). De plus, les estimations Ne, et en particulier celles liées aux générations antérieures, sont fortement affectées par des facteurs de manipulation des données, tels que le choix des valeurs CRG et alpha. De plus, la stratégie de binning appliquée peut interférer avec la précision générale de la méthode, par exemple lorsqu’un nombre insuffisant de comparaisons par paires est utilisé pour remplir chaque bin.
Une des applications de la méthode est de comparer les démographies des races. Dans ce cas, la forme des courbes Ne serait l’outil optimal pour différencier différentes histoires démographiques, plus que leurs valeurs numériques, en les utilisant comme empreinte démographique potentielle pour cette race ou cette espèce, tout en tenant compte du fait que la mutation, la migration et la sélection peuvent influencer l’estimation de Ne par LD (Waples et Do, 2010). De plus, un examen attentif des données analysées avec le SNeP (et d’autres logiciels d’estimation de Ne) est très important, car la présence de facteurs de confusion tels que le mélange peut entraîner des estimations biaisées de Ne (Orozco-terWengel et Bruford, 2014).
L’objectif du SNeP est donc de fournir un outil rapide et fiable pour appliquer les méthodes LD afin d’estimer Ne en utilisant des données génotypiques à haut débit de manière plus cohérente. Il permet deux approches d’estimation r2 différentes ainsi que la possibilité d’utiliser des estimations r2 provenant d’un logiciel externe. L’utilisation du SNeP ne dépasse pas les limites de la méthode et de la théorie qui la sous-tend, mais il permet à l’utilisateur d’appliquer la théorie en utilisant toutes les corrections suggérées à ce jour.
Contributions de l’auteur
MB a conçu et écrit le logiciel et le manuscrit. MB, MT et POtW ont testé le logiciel et effectué les analyses. MT, POtW et MWB ont révisé le manuscrit. Tous les auteurs ont approuvé le manuscrit final.
Déclaration sur les conflits d’intérêts
Les auteurs déclarent que la recherche a été menée en l’absence de relations commerciales ou financières pouvant être interprétées comme un conflit d’intérêts potentiel.
Remerciements
Nous remercions Christine Flury pour avoir fourni les données sur les moutons et pour les discussions utiles. Nous remercions également les deux examinateurs pour leurs suggestions utiles pour améliorer ce document. MB a été soutenu par le programme Master and Back (Regione Sardegna).
Charlesworth, B., Nordborg, M., et Charlesworth, D. (1997). The effects of local selection, balanced polymorphism and background selection on equilibrium patterns of genetic diversity in subdivised populations. Genet. Rés. 70, 155 à 174. doi: 10.1017/S0016672397002954
Résumé PubMed /Texte intégral/ Texte intégral croisé / Google Scholar
Crow, J. F., et Kimura, M. (1970). Une Introduction à la Théorie de la Génétique des populations. New York, NY: Harper et Row.
Google Scholar
Ohta, T., et Kimura, M. (1971). Déséquilibre de liaison entre deux sites nucléotidiques en ségrégation sous le flux constant de mutations dans une population finie. Génétique 68, 571-580.
Résumé publié par PubMed | Texte intégral /Google Scholar
Wright, S. (1943). Isolement par distance. Génétique 28, 114-138.
Résumé PubMed / Texte intégral /Google Scholar