Filtres de Kalman

L’algorithme utilisé pour fusionner les données s’appelle un filtre de Kalman.

Le filtre de Kalman est l’un des algorithmes les plus populaires dans la fusion de données. Inventé en 1960 par Rudolph Kalman, il est maintenant utilisé dans nos téléphones ou satellites pour la navigation et le suivi. L’utilisation la plus célèbre du filtre a eu lieu lors de la mission Apollo 11 pour envoyer et ramener l’équipage sur la lune.

Quand utiliser un filtre Kalman ?

Un filtre de Kalman peut être utilisé pour la fusion de données pour estimer l’état d’un système dynamique (évoluant avec le temps) dans le présent (filtrage), le passé (lissage) ou le futur (prédiction). Les capteurs embarqués dans les véhicules autonomes émettent des mesures parfois incomplètes et bruyantes. L’imprécision des capteurs (bruit) est un problème très important et peut être traitée par les filtres Kalman.

Un filtre de Kalman est utilisé pour estimer l’état d’un système, noté x. Ce vecteur est composé d’une position p et d’une vitesse v.

A chaque estimation, on associe une mesure d’incertitude P.

En effectuant une fusion de capteurs, on prend en compte différentes données pour un même objet. Un radar peut estimer qu’un piéton est à 10 mètres tandis que le Lidar l’estime à 12 mètres. L’utilisation de filtres Kalman vous permet d’avoir une idée précise pour décider combien de mètres est vraiment le piéton en éliminant le bruit des deux capteurs.

Un filtre de Kalman peut générer des estimations de l’état des objets qui l’entourent. Pour faire une estimation, il n’a besoin que des observations actuelles et de la prédiction précédente. L’historique des mesures n’est pas nécessaire. Cet outil est donc léger et s’améliore avec le temps.

À quoi cela ressemble

L’état et l’incertitude sont représentés par des Gaussiens.

Une Gaussienne est une fonction continue sous laquelle l’aire est égale à 1. Cela nous permet de représenter les probabilités. Nous sommes sur une probabilité de distribution normale. L’uni-modalité des filtres de Kalman signifie que nous avons un seul pic à chaque fois pour estimer l’état du système.

Nous avons une moyenne μ représentant un état et une variance σ2 représentant une incertitude. Plus la variance est grande, plus l’incertitude est grande.

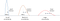
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Nous utilisons les observations de nos capteurs pour corriger l’état prédit et obtenir une estimation plus précise.

Pour faire une estimation, un filtre de Kalman n’a besoin que des observations actuelles et de la prédiction précédente. L’historique des mesures n’est pas nécessaire.

Maths

Les mathématiques derrière les filtres de Kalman sont faites d’additions et de multiplications de matrices. Nous avons deux étapes: la prédiction et la mise à jour.

Prédiction
Notre prédiction consiste à estimer un état x’ et une incertitude P’ à l’instant t à partir des états précédents x et P à l’instant t-1.

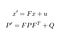
• F: Matrice de transition de t-1 à t
• ν: Bruit ajouté
• Q: Matrice de covariance incluant le bruit

Mise à jour
La phase de mise à jour consiste à utiliser une mesure z d’un capteur pour corriger notre prédiction et ainsi prédire x et P.

• y: Différence entre la mesure réelle et la prédiction, c’est-à-dire l’erreur.
• S : Erreur système estimée
• H : Matrice de transition entre le marqueur du capteur et le nôtre.
• R: Matrice de covariance liée au bruit du capteur (donnée par le fabricant du capteur).
• K: Gain de Kalman. Coefficient entre 0 et 1 reflétant la nécessité de corriger notre prédiction.

La phase de mise à jour permet d’estimer un x et un P plus proches de la réalité que ce que les mesures fournissent.

Un filtre de Kalman permet des prédictions en temps réel, sans données au préalable. Nous utilisons un modèle mathématique basé sur la multiplication des matrices pour définir à chaque fois un état x (position, vitesse) et une incertitude P.

Représentation Prior/Posterior

Ce diagramme montre ce qui se passe dans un filtre de Kalman.

• L’estimation de l’état prédit représente notre première estimation, notre phase de prédiction. Nous parlons de prior.
• La mesure est la mesure de l’un de nos capteurs. Nous avons une meilleure incertitude mais le bruit des capteurs en fait une mesure toujours difficile à estimer. Nous parlons de probabilité.
• L’estimation optimale de l’état est notre phase de mise à jour. L’incertitude est cette fois la plus faible, nous avons accumulé des informations et permis de générer une valeur plus sûre qu’avec notre capteur seul. Cette valeur est notre meilleure estimation. On parle de postérieur.

Ce qu’un filtre de Kalman implémente est en fait une règle de Bayes.

Dans un filtre de Kalman, nous bouclons les prédictions à partir des mesures. Nos prédictions sont toujours plus précises puisque nous gardons une mesure d’incertitude et calculons régulièrement l’erreur entre notre prédiction et la réalité. Nous sommes capables à partir de multiplications matricielles et de formules de probabilité d’estimer les vitesses et les positions des véhicules autour de nous.

Filtres « étendus/Non parfumés » et non-linéarité

Un problème essentiel se pose. Nos formules mathématiques sont toutes implémentées avec des fonctions linéaires de type y = ax +b.
Un filtre de Kalman fonctionne toujours avec des fonctions linéaires. En revanche, lorsque nous utilisons un radar, les données ne sont pas linéaires.

Le Radar voit le monde avec trois mesures:

Ces trois valeurs rendent notre mesure non linéaire compte tenu de l’inclusion de l’angle φ.

Notre objectif ici est de convertir les données ρ, φ, ρ en données cartésiennes (px, py, vx, vy).

Si nous entrons des données non linéaires dans un filtre de Kalman, notre résultat n’est plus sous forme gaussienne unimodale et nous ne pouvons plus estimer la position et la vitesse.

Nous utilisons donc des approximations, c’est pourquoi nous travaillons sur deux méthodes:
– Les filtres de Kalman étendus utilisent des séries Jacobiennes et de Taylor pour linéariser le modèle.
– Les filtres de Kalman non parfumés utilisent une approximation plus précise pour linéariser le modèle.

Pour traiter l’inclusion de la non-linéarité par le Radar, des techniques existent et permettent à nos filtres d’estimer la position et la vitesse des objets que nous souhaitons suivre.