HeheHe On nous a appris à multiplier de haut en bas par le conjugué du dénominateur. Ce conjugué est obtenu en remplaçant $-$ par $+$ (ou vice-versa) dans le dénominateur:

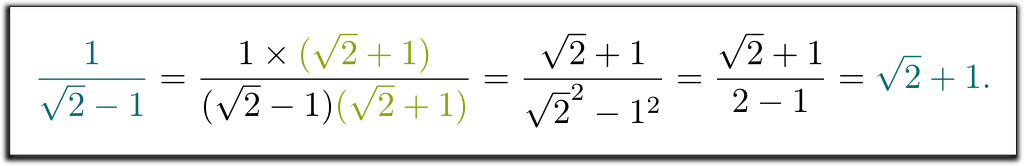
Je sais! L’expression compliquée $1/(\sqrt{2}-1) represents représente le même nombre que $\sqrt{2} + 1$. Et cela explique pourquoi nos professeurs voulaient que nous écrivions les résultats d’une manière plutôt que de l’autre: Lorsque tout est écrit de la même manière, les examens deviennent beaucoup plus faciles à corriger!

Mais qu’en est-il de $1/(\sqrt{2}-1)$? Pouvez-vous vous débarrasser de la racine dans le dénominateur? Peut-on même le faire?

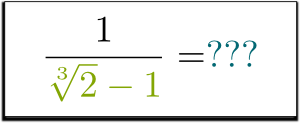
Je sais!

Tu me dis !

Une chance ?

Hehe Interestingly Fait intéressant, toute puissance de\\sqrt{2}-1 can peut être écrite comme une somme de puissances de $\sqrt{2}$. En effet, il suffit de distribuer les produits :

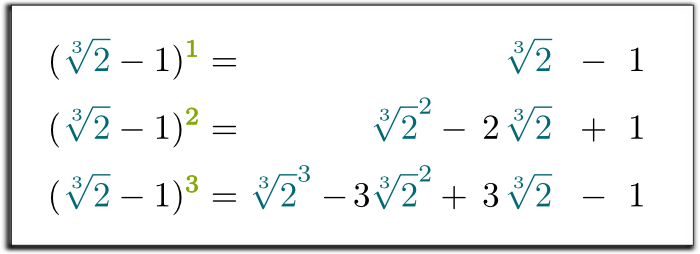
Oui c’est le cas ! En procédant de cette substitution dans la troisième équation, nous avons montré que les trois premières puissances de $\sqrt{2}-1$ peut être écrit comme une somme d’un nombre rationnel, de $\sqrt{2}$ et de $\sqrt{2}^2$!

Nous avons donc maintenant 3 équations, avec 2 expressions racines dont nous voulons nous débarrasser! Ainsi, nous pouvons combiner les équations pour supprimer toutes les expressions racines à droite!

Multiplions les 2 premières lignes par 3 et additionnons les 3 équations:

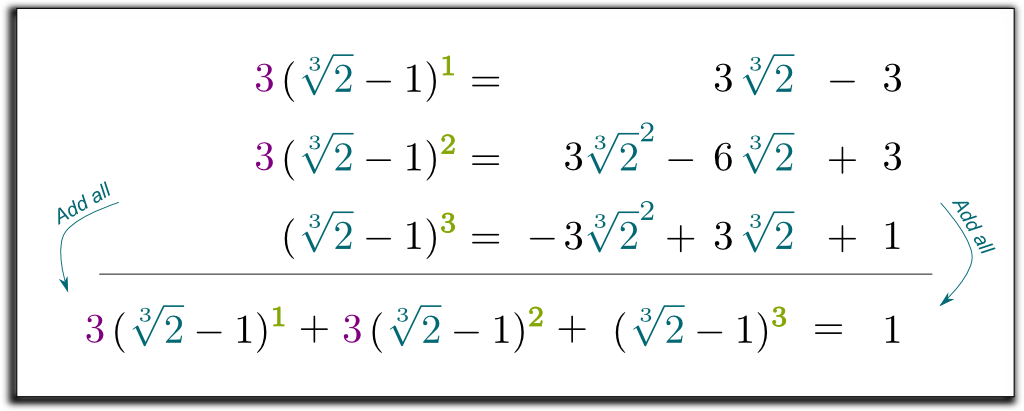
Hehe The Ce qui est cool, c’est que le terme de gauche que nous avons obtenu peut maintenant être factorisé par $\sqrt{2}-1!! Laissez-moi sauter quelques calculs ennuyeux And Et arriver au résultat $(\sqrt{2}-1)((\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Donc, pour se débarrasser des racines dans le dénominateur, nous pouvons multiplier de haut en bas par\\sqrt{2}^2 +\sqrt{2} + 1$! Enfin, nous obtenons la formule surprenante et belle suivante:

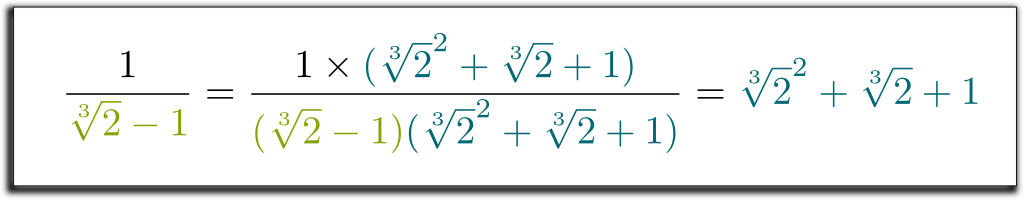
Je sais! Mais ce qui est encore plus net, c’est que la méthode que nous avons utilisée est très générale! Avec des techniques similaires, nous pouvons maintenant supprimer tous les radicaux des dénominateurs!

Ce qui intéressait particulièrement Galois, ce n’était pas le fait qu’une méthode permettait d’éliminer les radicaux des dénominateurs. Mais plutôt, que tout nombre avec des radicaux dans les dénominateurs égalait un nombre avec des radicaux sur le dessus. Cela signifiait que les nombres avec des radicaux au-dessus étaient stables par division.

Il est courant de désigner $\mathbb Q{2}] the l’ensemble des nombres qui peuvent être écrits comme une somme de puissances de\\sqrt{2}$. Puisque $\sqrt{2}^3 = 2$ est un nombre rationnel, une somme de puissances de $\sqrt{2}$ peut en fait être écrit dans le standard de la forme $a\sqrt{2}^2 + b\sqrt{2} + c$. Maintenant, si vous ajoutez, soustrayez ou multipliez deux de ces nombres, il n’est pas difficile de voir que nous obtenons des nombres qui peuvent toujours être mis sous la forme standardaa \sqrt{2}^2 + b\sqrt{2} + c$. De plus, ce que nous venons de montrer ici, c’est que l’inverse de tous les nombresaa \sqrt{2}^2 + b \ sqrt{2} + c can peut également être écrit sous forme standard. Cela montre que toute addition, soustraction, multiplication et division de nombres dans $\mathbb Q{2}] yields donne un nombre, qui peut être écrit sous forme standard and et appartient donc à $\mathbb Q{2}]$. En termes d’algèbre pure, $\mathbb Q{2}] is est donc stable par les quatre opérations arithmétiques classiques. Pour cette raison, nous appelons cela un champ.

Géométrie des extensions de champs

Le champ que vous connaissez le plus est probablement l’ensemble Q\mathbb Q Q des nombres rationnels. D’autres exemples de champs sont les ensembles R\mathbb R of de nombres réels et l’ensemble C\mathbb C C de nombres complexes. Et maintenant, nous avons aussimath\mathbb Q{2}]$. Puisque $\mathbb Q{2}]$ est un champ qui contient le champ de $\mathbb Q$, on dit que $\mathbb Q{2}] / \mathbb Q$ est un champ d’extension.

Le fait que $\mathbb Q{2}]/\mathbb Q is soit une extension de champ donne une connexion très naturelle entre les deux champs. À savoir, can\mathbb Q{2}] can peut être vu comme un espace vectoriel, où $\mathbb Q is est le champ scalaire. En particulier, le fait que tout nombre dans $\mathbb Q{2}]$ peut être écrit $a \sqrt{2}^2 + b\sqrt{2} + c$ signifie que $(1, \sqrt{2}, \sqrt{2}^2)$ une base de $\mathbb Q{2}]$ en $\mathbb Q$-espace vectoriel. Et cela signifie que nous pouvons le représenter géométriquement comme un espace à 3 dimensions!

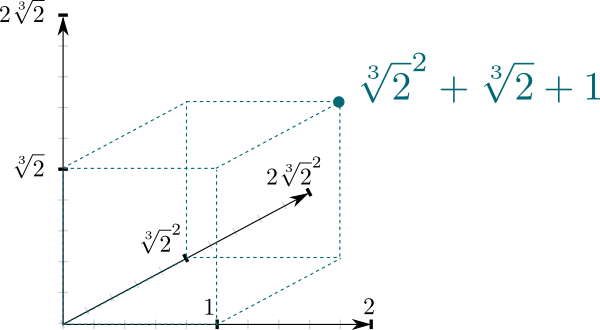
La dimension de l’espace vectoriel ci-dessus est une propriété intéressante des extensions de champ. Il est connu sous le nom de degré, et il est généralement notébig\big {2}]: \mathbb Q \big] = 3 = par exemple.

Oui! Il est en fait assez facile de créer une extension de champ de ceci: Ajoutez simplement un nombre radical qui n’appartient pas à $\mathbb Q{2}]$!

Oui! Cela créerait le champ $(\mathbb Q{2}]) = \mathbb Q{2}, \sqrt{2}]$. Ces champs contiennent tous les nombres qui sont des produits et des sommes de\\sqrt{2} and et\\sqrt{2}$. Ces sont de la forme $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Une idée du degré is\big{2}, \sqrt{2}]: \mathbb Q{2}]\big] is est-elle?

Oui! En effet, nous avons $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $ + $d\sqrt{2}^2 + e \sqrt{2} + f) \sqrt{2}$. Ainsi, un nombre quelconque de $\mathbb Q{2},\sqrt{2}]$ peut être écrit $A+B\sqrt{2}$, où $A$ et $B$ appartient à $\mathbb Q{2}]$. Ainsi, 2 scalaires de $\mathbb Q{2}] determine déterminent un nombre dans $\mathbb Q{2}, \sqrt{2}]$. Cela signifie que le degré de l’extension de champ\\mathbb Q{2}, \sqrt{2}]/\mathbb Q{2}] is est 2. En fait, nous avons la relation de Chaslesbig\big{2}, \sqrt{2}]: \mathbb Q\big]= =big\big{2}, \sqrt{2}] : \mathbb Q {2}] \big]\big {2}]: \mathbb Q\big]= = 22\ fois 3 = 6 6.

C’est mieux que ça ! Toute extension de champ de degré fini, appelée extension de champ fini, est étendue par un seul nombre. Par exemple $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, ce qui signifie que tous les nombres qui sont des sommes de puissances de $\sqrt{2}$ et $\sqrt{2}$ sont aussi des sommes de puissances de $\sqrt{2} + \sqrt{2}$. N’est-ce pas étonnamment génial?

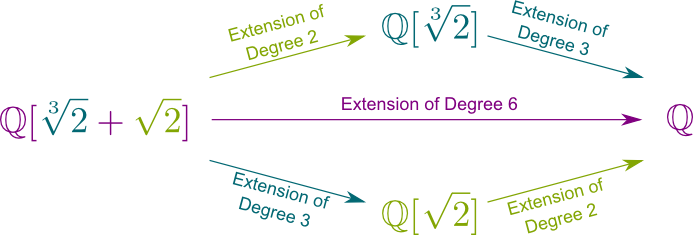
de manière Plus générale, tout de galois de l’extension de $\mathbb Q$ peut être écrit $\mathbb Q$ certains $x$ qui est ajouté à $\mathbb Q$.

Oui. C’est le cas pour l’extension de champ\\mathbb R/\mathbb Q Q. Et, il en est de même de l’extension de champ la plus importante de la théorie de Galois! Cette extension de champ est $\bar {\mathbb Q} /\mathbb Q,, où $\bar{\mathbb Q} is est l’ensemble des nombres algébriques. Ce sont toutes des solutions à des équations polynomiales de la forme $a_n x^n $ + a a_{n-1} x^{n-1} $+$ … $+$ a_1 x x + a a_0 = 0$. Par exemple,\\sqrt{2} is est un nombre algébrique car il est solution àxx^4-2x = 0$. Ainsi, $\bar {\mathbb Q} is est une extension de champ à toutes les extensions de champ fini de Q\mathbb Q$.

Nombres conjugués

Nous y sommes presque ! Nous avons besoin d’un dernier détour par les équations polynomiales.

Exactement! Galois a remarqué que certaines équations pouvaient être simplifiées. Par exemple, $x^4-2x=0$ peut être factorisée comme $x(x^3-2)=0$, ce qui correspond à $x=0$ ou $x^3-2=0$. Donc, l’équation $x^4-2x=0$ peut être réduite à des équations $x=0$ et $x^3-2=0$. Et en fait, cette réduction est très similaire à la façon dont des nombres comme 35 peuvent être réduits à 5 et 7, car55 \ fois 7 = 35$. La similitude entre les équations et les nombres entiers est si forte que nous pouvons même faire des divisions euclidiennes de polynômes, tout comme vous avez appris à le faire pour les nombres! À droite, un exemple d’une telle division (ne vous inquiétez pas si vous ne le comprenez pas, ce ne sera pas important pour la suite).

Exactement! Celles-ci sont connues sous le nom d’équations polynomiales irréductibles. L’équation $x^3-2 = 0 is est un exemple d’équation polynomiale irréductible.

Oui! Mais, surtout, Galois voulait se concentrer sur les équations à coefficients rationnels. Ou plutôt des polynômes à coefficients appartenant au champ de base. Donc, ce que je voulais dire, c’est que, pour $\mathbb Q as comme champ de base,xx^3-2 = 0 is est irréductible.

Considérons $x^2-2x-1=0$ pour avoir quelques indices. Cette équation peut être prouvée irréductible. Vous souvenez-vous comment le résoudre?

Sibb^2-4ac\geq 0$, oui.

Exactement! Ainsi, le polynôme irréductible de l’équation $x^2 + 2x -1=0$ a deux solutions: $1+\sqrt{2}$ et $1-\sqrt{2}$… un commentaire?

Bingo! C’est la découverte clé de Galois. Plus généralement, Galois dit conjugue toutes les solutions à une équation polynomiale irréductible. Et, comme vous pouvez l’imaginer, ceux-ci sont essentiels pour éliminer les radicaux des dénominateurs!

La première chose à remarquer est que si $x_1$, $x_2$, …, $x_n$ sont toutes les solutions d’un polynôme irréductible de l’équation $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ à coefficients rationnels, alors ce polynôme irréductible équation peut effectivement être réécrite $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. L’identification des termes constants donne alors $x_1 x_2 xx_n= = ((-1) ^n a_0/a_n$. Donc, de manière cruciale, le produit des nombres conjugués est le nombre rationnel^(-1) ^n a_0 /a_n,, qui est non nul (prouvez-le!).

Voici une petite blague pour garder à l’esprit le lien fort entre les conjugués:

Considérons une fraction $1/x_1,, où $x_1 is est une expression compliquée avec des radicaux. En multipliant en haut et en bas par les conjugués $x_2$, …, $x_n$ de $x_1$, alors les rendements de 1 $x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, ce qui n’a pas de radical au dénominateur, comme nous l’avons établi $a_0$ pour un non-nulle du champ de base!

Rappelons que $x^3-2 = 0 is est l’équation polynomiale irréductible\\sqrt{2} is est la solution de. Ainsi, ses conjugués sont les autres solutions à cette équation, qui sont les nombres complexes $\sqrt{2}j$ et $\sqrt{2}j^2$, où $j= e^{i\tau/3}$ avec $\tau = 2\pi$ étant le rapport entre la circonférence d’un cercle par son rayon. La figure suivante montre les emplacements des solutions conjuguées dans ce plan complexe :

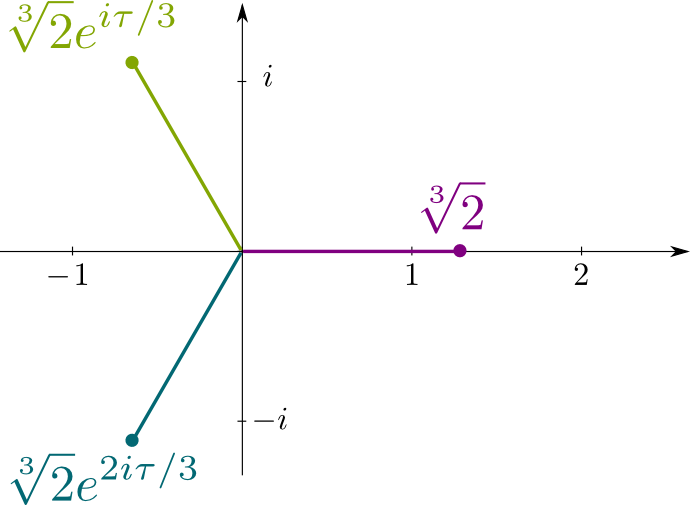
Ambiguïté de Galois

Enfin, nous arrivons à l’aperçu clé de Galois!

sont parfaitement permutables. Cela signifie que, si vous changez systématiquement $\sqrt{2} by par son conjugué $-\sqrt{2},, alors les égalités tiennent toujours. Par exemple, puisque nous avions $1/(\sqrt{2}-1) = \sqrt{2} + 1$, je peux vous dire directement que $1/(-\sqrt{2}-1) = -\sqrt{2} +1$! De même, nous avons l’implication étonnante suivante:

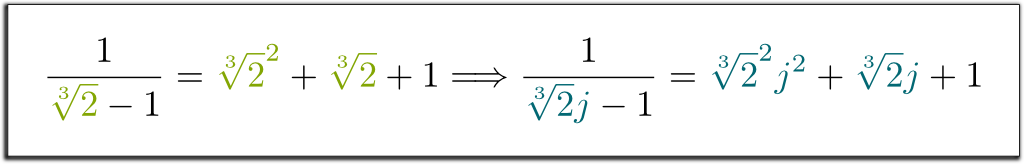
Hehe Let Permettez-moi d’abord de rappeler que les champs finis sont couverts par un seul élément. Donc, si le champ de base est de $\mathbb Q$, tout corps fini peut être écrit $\mathbb Q$ pour un droit de $x_1$. Maintenant, envisager de $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ le polynôme irréductible de l’équation $x_1$ est la solution. Ensuite, ce qui définit $\mathbb Q$ est $\mathbb Q$-espace vectoriel engendré par $x_1$, $x_1^2$, …, $x_1^{n-1}$, avec la simplification des pouvoirs accrus de $x_1$ en conséquence de la règle algébrique $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

Exactement! Surtout, ces algébrique des règles de $\mathbb Q$ n’ont pas vraiment dépend de la nature de $x_1$; ils dépendent uniquement de l’irréductible polynôme $x_1$ est la solution de! Par conséquent, les règles de $\mathbb Q$ sont identiques à ceux de $\mathbb Q$, …, $\mathbb Q$, où $x_1$ est remplacé par l’un de ses conjugués $x_2$, …, $x_n$. En particulier, les champs\\mathbb Q{2}] and et\\mathbb Q{2}j] operate fonctionnent exactement selon les mêmes règles. C’est pourquoi les conjugués sont parfaitement permutables ! Nous disons que les champs de $\mathbb Q{2}]$ et $\mathbb Q{2} j]$ est isomorphe, et que le remplacement de $\sqrt{2}$ par $\sqrt{2}j$ est un isomorphisme $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

D’une manière très similaire (mais plus forte) que deux espaces vectoriels de dimension 2 sont plus ou moins les mêmes! Cela a une conséquence terrible. Cela signifie que, d’un point de vue algébrique, il n’a aucun sens de faire une différence entre un nombre et l’un de ses conjugués (à condition de remplacer systématiquement le nombre par son conjugué)! Ainsi, par exemple, $\sqrt{2} and et and-\sqrt{2} are sont algébriquement indiscernables ! Pour garder cela à l’esprit, voici une autre blague que j’ai inventée:

Pas du tout ! Toute distinction entre ces deux nombres doit impliquer d’autres mathématiques que l’algèbre, comme les relations d’ordre ou la topologie. Ce que je veux dire, c’est que, par exemple, la relation $\sqrt{2} > 0$ t faire une différence entre $\sqrt{2}$ en $-\sqrt{2}$, mais c’est parce qu’il s’agit d’une relation d’ordre. Mais si nous nous limitons aux égalités polynomiales, il n’y a absolument aucune différence entre $\sqrt{2} and et $-\sqrt{2}$. De même, $i$ et $-i$, les solutions du polynôme irréductible de l’équation $x^2+1=0$, sont également algébriquement indiscernables. Pourtant, nous appelons arbitrairementi je one l’un d’entre eux. C’est pourquoi Galois a appelé sa théorie la théorie de l’ambiguïté. Aujourd’hui, l’ambiguïté du choix de la classique de la racine carrée de $-1$ parmi $i$ et $-i$ est plutôt appelé la symétrie entre $i$ et $-i$.

Groupes de Galois

Galois s’est particulièrement concentré sur les extensions de champ qui sont stables par conjugaison. De telles extensions de champs stables sont maintenant connues sous le nom d’extensions de Galois. Donc, si $x_1$ appartient à un de Galois de l’extension, puis ce de Galois de l’extension contient tous ses conjugués $x_2$, …, $x_n$.

Une façon simple de construire des extensions de Galois consiste à prendre le champ couvert par des solutions d’une équation polynomiale irréductible. Par exemple, si $x_1$, …, $x_n$ sont conjugués pour le champ de base de $\mathbb Q$, alors $\mathbb Q / \mathbb Q$ est un de Galois de l’extension. Les champs construits de cette façon sont appelés champs de fractionnement.

Par exemple, le champ de division de l’équationxx^3-2 =0 is est l’extension de Galois $\mathbb Q{2}, \sqrt{2}j, \sqrt{2}j^2]/\mathbb Q span étendue par ses solutions.

Si $x_1 spans couvre une extension de Galois, ses conjugués aussi. Ainsi, $\mathbb Q = \mathbb Q =$ … $= \mathbb Q = =\\mathbb Q$. Ainsi, l’isomorphisme entre $\mathbb Q$ et $\mathbb Q$ qui consiste à toujours remplacer $x_1$ par $x_2$ est en fait un isomorphisme entre $\mathbb Q$ et de lui-même! Nous appelons cela un automorphisme. Les automorphismes d’une extension de Galois forms\mathbb Q/\mathbb Q forms forment le groupe de GaloisGalGal(\mathbb Q/\mathbb Q)$.

Maintenant, il est crucial, si $\mathbb Q = \mathbb Q$, alors tous les automorphismes de Galois de l’extension $\mathbb Q/ \mathbb Q$ sont des permutations de $x_1$ avec l’un de ses conjugués! En particulier, nous voyons ici que la cardinalité d’un groupe de Galois est égale au degré de l’extension de Galois.

Bien sûr! Vous pouvez remarquer que $\mathbb Q = \mathbb Q$ et $\mathbb Q = \mathbb Q$, ce qui signifie que $i$ et $\sqrt{2}$ chacun s’étend sur le fractionnement des champs de l’irréductible équation polynomiale ils sont la solution de. Ainsi, $\mathbb Q/\mathbb Q and et $\mathbb Q/\mathbb Q are sont toutes deux des extensions de Galois. Par conséquent, leurs automorphismes consister à remplacer $i$ par l’un de ses conjugués, $i$ ou $-i$, et le remplacement de $\sqrt{2}$ par $\sqrt{2}$ ou $-\sqrt{2}$. Dans les premiers cas, nous ne changeons rien en nombres, ce qui correspond à la symétrie nulle. Les seconds cas peuvent être visualisés sous forme de symétries axiales, comme indiqué dans la figure ci-dessous:

N’est-ce pas incroyable?

Bien sûr! Passons au champ de division Q\mathbb Q{2}, \sqrt{2}j, \sqrt{2}j^2] of dexx^3-2 = 0$. Mais, avant d’aller plus loin, notons que $\mathbb Q{2}, \sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.

Il suffit de prouver que tous les générateurs d’un champ appartiennent à l’autre. Commençons par prouver que les générateurs de ce dernier, $\sqrt{2} and etjj$, appartiennent au premier. C’est évident pour $\sqrt{2}$. Maintenant,jj =(\sqrt{2}j) / \sqrt{2}$, doncjj belong appartiennent également à l’ancien champ. Cela prouve que tous les éléments demath\mathbb Q{2}, j] belong appartiennent à $\mathbb Q{2}, \sqrt{2}j, \sqrt{2} j^2]$. Réciproquement, il est simple que tous les producteurs de l’ancien champ, $\sqrt{2}$, $\sqrt{2}j$ et $\sqrt{2}j^2$, sont les produits de l’générateurs de ce dernier. Ainsi, les deux champs sont égaux. Et, en particulier,\\mathbb Q{2}, j]/\mathbb Q is est une extension de Galois.

Hehe ToPour comprendre les symétries de Q\mathbb Q{2}]$, nous devrons aller plus loin dans l’étude de Galois des groupes de Galois

Correspondance de Galois

Le problème avec les groupes de Galois est qu’ils peuvent devenir extrêmement grands et compliqués. C’est notamment le cas du groupe infiniGalGal(\bar{\mathbb Q}/\mathbb Q)$. Pour appréhender des groupes aussi immenses et complexes, Galois a eu la brillante idée de les découper en petits morceaux.

Étonnamment, Galois a découvert que les groupes de Galois pouvaient être divisés en sous-groupes de symétries en ne regardant que ceux qui laissent un sous-champ inchangé. Par exemple,\\mathbb Q is est un sous-champ de $\mathbb Q{2}, j],, puisque tout nombre du premier appartient au second. Ainsi, les symétries de $\mathbb Q{2},j]$ qui ne sont pas de changer quoi que ce soit de $\mathbb Q$ forment un sous-groupe du groupe de Galois de $\mathbb Q{2},j]/\mathbb Q$. Ces symétries forment le groupe de GaloisGalGal(\mathbb Q{2},j]/\mathbb Q)$.

Je sais! J’aime visualiser ces symétries comme les moyens de brancher $\mathbb Q{2}, j] onto sur onto\mathbb Q$. Voici une image imagée du « branchement sur »:

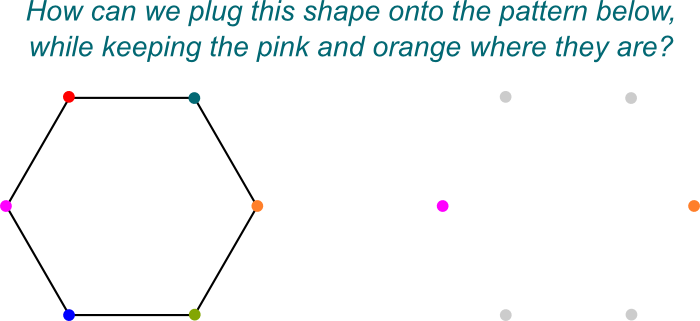
Exactement! Et c’est tout simplement parce que $\mathbb Q{2},j]$ est un de Galois de l’extension de $\mathbb Q$ qui est lui-même un champ d’extension de $\mathbb Q$.

Et il y a plus! Galois a montré que tous les sous-groupes d’une extension de Galois sont obtenus de cette façon ! Plus précisément, la cartographie d’un champ $K$ entre le Galois de l’extension $\mathbb Q{2},j]$ et le champ de base de $\mathbb Q$ pour le groupe de Galois $Gal(\mathbb Q{2},j] / K)$ est bijective. Ce fait s’appelle la correspondance de Galois ! Cette correspondance est schématiquement affichée ci-dessous pour une extension de Galois $\mathbb Q/\mathbb Q$.

Au lieu d’essayer de décrire directement ce groupe, concentrons-nous sur son sous-groupeGalGal(\mathbb Q{2},j]/\mathbb Q)$. Il est simple que $\sqrt{2}$ s’étend sur $\mathbb Q{2},j]$ lorsqu’il est ajouté à $\mathbb Q$. Ainsi, $\mathbb Q{2}, j]/\mathbb Q is est une extension de Galois étendue par $\sqrt{2}$. Par conséquent, en utilisant un théorème que nous l’avons vu précédemment, nous savons que tous les automorphismes de ce de Galois de l’extension consister à remplacer $\sqrt{2}$ par l’un de ses 3 conjugués (lui-même, $\sqrt{2} j$ et $\sqrt{2} j^2$)!

Maintenant, je pourrais continuer à étudier d’autres morceaux deGalGal(\mathbb Q{2},j]/\mathbb Q)$, comme le sous-groupe de GaloisGalGal(\mathbb Q{2},j]/\mathbb Q{2}])$. Mais je préfère utiliser un autre des puissants théorèmes de Galois. À savoir, il a prouvé que si $\mathbb Q /\mathbb Q was était en outre une extension de Galois elle-même, alors le sous-groupeGalGal(\mathbb Q{2}, j]/\mathbb Q) is est normal.

Ainsi, le groupe de Galois de $\mathbb Q{2},j]/\mathbb Q can peut être quotienté par ce sous-groupe, et le groupe de quotient est alors égal àGalGal(\mathbb Q/\mathbb Q)$. Pourtant, $\mathbb Q/\mathbb Q$ est en effet un de Galois de l’extension engendré par $j$, dont le conjugué est $j^2$. Ainsi, $Gal(\mathbb Q/\mathbb Q)$ est constitué soit en laissant $j$ que $j$ ou de le remplacer par $j^2$.

On peut maintenant déduire toutes les symétries de $Gal(\mathbb Q{2},j]/\mathbb Q)$ par la combinaison de ces de $Gal(\mathbb Q{2},j] / \mathbb Q)$ et $Gal(\mathbb Q/\mathbb Q)$. On peut afficher ces symétries par le dessin de la façon dont ils affectent nos trois couvrant conjugués de $\sqrt{2}$, $\sqrt{2}j$ et $\sqrt{2}j^2$:

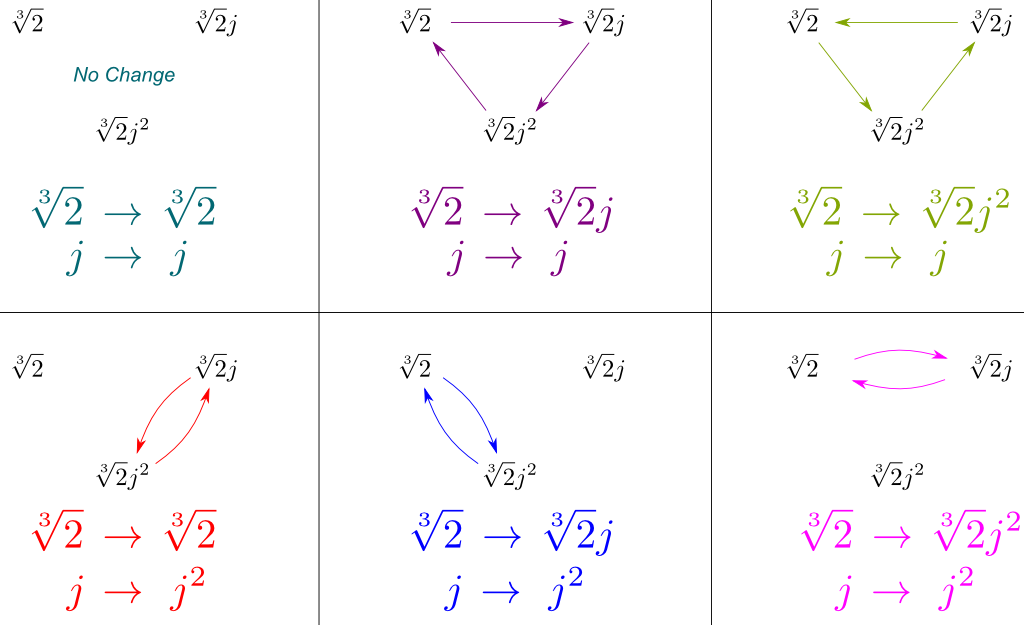
De manière cruciale, la figure ci-dessus contient toutes les symétries deGalGal(\mathbb Q{2},j]/\mathbb Q)$. Et étonnamment, ces symétries correspondent à un groupe de symétrie bien connu.

Je vais laisser Marcus du Sautoy vous le présenter:

Alors, les symétries sont-elles ici comme une étoile de mer ou comme un triangle?

Oui, en effet! Ce groupe de symétries du triangle est appeléDD_3$, et il est le même que le groupeSS_3 of de permutations de 3 éléments. Cela nous amène à la formule suivante, que j’ai trouvée si belle, que j’ai décidé de l’encadrer !

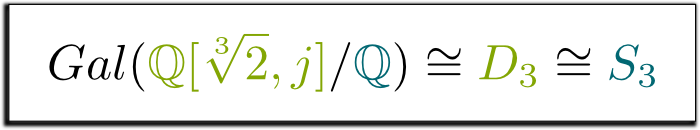
Concluons

À bien des égards, Galois doit être considéré comme le père de l’algèbre moderne. Son point de vue clé était de regarder les mathématiques sous l’angle des règles de fonctionnement, ce qui l’a amené à dévoiler des ambiguïtés surprenantes et perspicaces, ou symétries, entre les nombres. À partir d’un point de vue algébrique, les nombres tels que $\sqrt{2}$, $\sqrt{2}j$ et $\sqrt{2}j^2$ sont en effet parfaitement symétrique et totalement interchangeables.

La compréhension de ces symétries a eu des applications étonnantes en géométrie algébrique et en topologie algébrique, entre autres. En particulier, les premiers succès de la théorie incluent une classification des polygones réguliers constructibles et un théorème affirmant que les équations polynomiales de haut degré ne pouvaient pas être résolues par des radicaux.