Préalgèbre
Résultats d’apprentissage
- Trouvez l’aire, la base et la hauteur d’un triangle
- Trouvez la longueur d’un côté d’un triangle compte tenu du périmètre et de deux autres longueurs
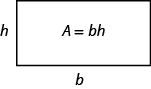
Nous savons maintenant comment trouver l’aire d’un rectangle. Nous pouvons utiliser ce fait pour nous aider à visualiser la formule de l’aire d’un triangle. Dans le rectangle ci-dessous, nous avons étiqueté la longueur b et la largeur h, donc sa zone est bh.
L’aire d’un rectangle est la base, b, fois la hauteur, h.
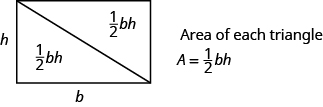
On peut diviser ce rectangle en deux triangles congruents (voir l’image ci-dessous). Les triangles congruents ont des longueurs et des angles latéraux identiques, et leurs aires sont donc égales. L’aire de chaque triangle est la moitié de l’aire du rectangle, ou \frac{1}{2}bh. Cet exemple nous aide à voir pourquoi la formule de l’aire d’un triangle est A = \frac{1}{2}bh.
Un rectangle peut être divisé en deux triangles d’aire égale. L’aire de chaque triangle est la moitié de l’aire du rectangle.
La formule de l’aire d’un triangle est A = \frac{1}{2}bh, où b est la base et h est la hauteur.
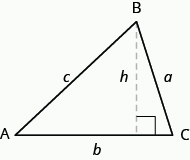
Pour trouver l’aire du triangle, vous devez connaître sa base et sa hauteur. La base est la longueur d’un côté du triangle, généralement le côté en bas. La hauteur est la longueur de la ligne qui relie la base au sommet opposé et fait un angle \text{90}^\circ avec la base. L’image ci-dessous montre trois triangles avec la base et la hauteur de chacun marqués.
La hauteur h d’un triangle est la longueur d’un segment de ligne qui relie la base au sommet opposé et fait un angle \text{90}^\circ avec la base.

Propriétés du triangle
Pour tout triangle \Delta ABC, la somme des mesures des angles est \text{180}^\circ.
m\angle {A} + m\angle {B} + m\angle{C} = 180^\circ
Le périmètre d’un triangle est la somme des longueurs des côtés.
P= a +b +c
L’aire d’un triangle est la moitié de la base, b, fois la hauteur, h.
A= \frac{1}{2}bh
exemple
Trouvez l’aire d’un triangle dont la base est de 11 pouces et dont la hauteur est de 8 pouces.
Solution
| Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données. |  |
| Étape 2. Identifiez ce que vous recherchez. | l’aire du triangle |
| Étape 3. Nom. Choisissez une variable pour la représenter. | soit A = aire du triangle |
| Étape 4.Traduire.
Écrivez la formule appropriée. Substitut. |
 |
| Étape 5. Résolvez l’équation. | A = 44 pouces carrés. |
| Étape 6. Vérifiez :
A=\frac{1}{2}bh 44\stackrel {?} {=}\frac{1}{2}(11)8 44= 44\coche |
|
| Étape 7. Répondez à la question. | La superficie est de 44 pouces carrés. |
essayez-le
exemple
Le périmètre d’un jardin triangulaire est de 24 pieds. Les longueurs des deux côtés sont de 4 pieds et 9 pieds. Combien de temps dure le troisième côté?
essayez-le
exemple
La superficie d’une fenêtre d’église triangulaire est de 90 mètres carrés. La base de la fenêtre est de 15 mètres. Quelle est la hauteur de la fenêtre?
essayez-le
Triangles isocèles et équilatéraux
En plus du triangle rectangle, certains autres triangles ont des noms spéciaux. Un triangle avec deux côtés de longueur égale est appelé triangle isocèle. Un triangle qui a trois côtés de longueur égale est appelé triangle équilatéral. L’image ci-dessous montre les deux types de triangles.
Dans un triangle isocèle, deux côtés ont la même longueur et le troisième côté est la base. Dans un triangle équilatéral, les trois côtés ont la même longueur.
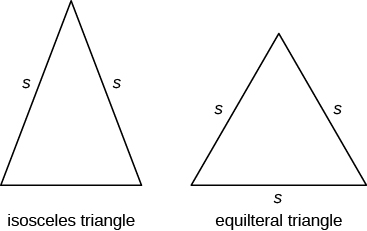
Triangles isocèles et équilatéraux
Un triangle isocèle a deux côtés de même longueur.
Un triangle équilatéral a trois côtés de longueur égale.
exemple
Le périmètre d’un triangle équilatéral est de 93 pouces. Trouvez la longueur de chaque côté.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. L’écharpe sera un triangle isocèle avec une base de
60 pouces. Combien de temps peut-elle faire les deux côtés égaux?








