Les antennes rayonnent de l’énergie électromagnétique pour transmettre ou recevoir des informations. Par conséquent, les termes Énergie et Puissance sont associés à ces ondes électromagnétiques et nous devons en discuter. Une onde électromagnétique a des champs électriques et magnétiques.

Considérez l’onde à tout instant, qui peut être visualisée dans les deux vecteurs. La figure suivante montre la représentation des composantes du champ électrique et magnétique dans une onde électromagnétique.

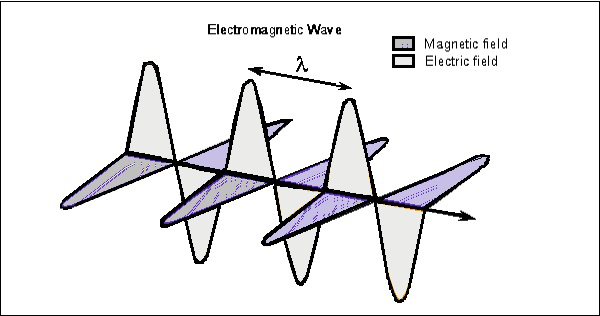
L’onde électrique est présente verticalement à la propagation de l’onde EM, tandis que l’onde magnétique est située horizontalement. Les deux champs sont perpendiculaires l’un à l’autre.

Vecteur de Poynting

Le vecteur de Poynting décrit l’énergie de l’onde EM par unité de temps par unité de surface à un instant donné. John Henry Poynting a dérivé ce vecteur pour la première fois en 1884 et il a donc été nommé d’après lui.

Définition − « Le vecteur de Poynting donne le taux de transfert d’énergie par unité de surface »

ou

« L’énergie qu’une onde transporte par unité de temps par unité de surface est donnée par le vecteur de Poynting. »

Le vecteur de Poynting est représenté par Ŝ.

Unités

L’unité SI du vecteur de Poynting est W/m2.

Expression mathématique

La quantité utilisée pour décrire la puissance associée aux ondes électromagnétiques est le vecteur de Poynting instantané, qui est défini comme

\\hat{S}=\hat{E}\times\hat{H}Où

• $\hat{S} is est le vecteur de Poynting instantané (W/m2).

• $\hat{E} is est l’intensité instantanée du champ électrique (V/m).

• $\hat{H} is est l’intensité instantanée du champ magnétique (A/m).

Le point important à noter ici est que la magnitude de E est supérieure à H dans une onde EM. Cependant, les deux apportent la même quantité d’énergie. Ŝ est le vecteur, qui a à la fois la direction et la magnitude. La direction de Ŝ est la même que la vitesse de l’onde. Sa magnitude dépend de la Dérivation E et H.

du Vecteur de Poynting

Pour avoir une idée claire du vecteur de Poynting, passons en revue la dérivation de ce vecteur de Poynting, dans un processus étape par étape.

Imaginons qu’une onde EM, passe une zone (A) perpendiculaire à l’axe des abscisses le long de laquelle l’onde se déplace. En passant par A, en temps infinitésimal (dt), l’onde parcourt une distance (dx).

$$dx = C\ dt$$

Où

$$C = vitesse\ de\ la lumière = 3\times 10^{8}m/s$$$$volume dv = Adx = AC\ dt$$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$= \epsilon_{0} AC \ E^{2}\ dt$$

Donc, l’Énergie transférée dans le temps (dt) par zone (A) −

$$S = \frac{l’Énergie}{Temps\times Zone} = \frac{dW}{dt\ A} = \frac{\epsilon_{0}ACE^{2}\ dt}{dt\ A} = \epsilon_{0}C\:E^{2}Since

Depuis

Since\frac{E}{H}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}\puis\S=\frac{CB^{2}}{\mu_{0}}$$

Depuis

CC=\frac{E}{H}\ puis\S =\frac{EB}{\mu_{0}}$$$$= \ hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H}) denotes

denotes désigne le vecteur de Poynting.

L’équation ci-dessus nous donne l’énergie par unité de temps, par unité de surface à un instant donné, appelée vecteur de Poynting.