Une partie intégrante de la dynamique des fluides est la vorticité. Heuristiquement, il mesure la rotation locale d’une parcelle de fluide. Pour les objets solides, nous ne parlons pas de la vorticité d’un objet mais de sa vitesse angulaire. Ces deux concepts sont liés mais la vorticité est plus utile lorsque l’on discute d’objets en rotation qui se déforment, comme le fait un fluide.

La vorticité d’un champ de vitesse donné dans un plan donné, est calculée en choisissant deux axes orthogonaux quelconques dans ce plan et en ajoutant la vitesse angulaire de chaque axe. Dans un objet solide, ou un fluide qui tourne comme un objet solide (bien nommé rotation du corps solide), la vorticité est deux fois la vitesse angulaire puisque chaque axe tourne à la même vitesse. Cependant dans un fluide les deux axes peuvent tourner à des vitesses très différentes et même des directions différentes! Il est même possible que chaque axe puisse tourner mais la vorticité nette est nulle (voir vortex irrotationnel).

Si le mouvement d’un fluide est strictement confiné dans un plan, le vecteur de vorticité est considéré comme orthogonal au plan et ne peut pas changer de direction (ou d’inclinaison). Le seul aspect de la vorticité qui peut changer est son ampleur. On pense que ce transfert d’énergie à de plus grandes échelles est lié à la formation de la Grande Tache rouge sur Jupiter.

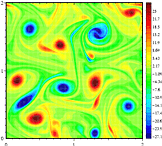
Dans un mouvement fluide tridimensionnel, le vecteur de vorticité est tridimensionnel en ce qu’il a des composantes parallèles à chaque axe, x, y et z: la composante z est parallèle à l’axe z et décrit la vitesse de rotation dans le plan xy. C’est à cause de cette dichotomie qu’il existe une différence qualitative de comportement entre la turbulence bidimensionnelle et la turbulence tridimensionnelle. Dans le premier cas, les tourbillons ont tendance à s’agglutiner et à former de plus grands tourbillons, tandis que dans le second, les mouvements tourbillonnaires sont déchirés et l’énergie tombe en cascade jusqu’aux plus petites échelles où elle est ensuite diffusée.

Mathématiquement, la vorticité d’un champ de vitesse donné,

est définie comme la boucle du champ de vitesse, et est généralement désignée par la lettre grecque omega,

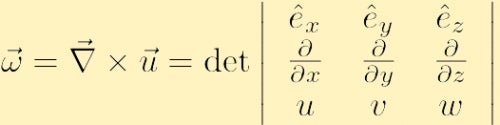
où nous avons utilisé le symbole nabla conventionnel pour le dégradé:

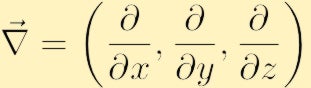
Sous forme de composant, la vorticité est trouvée en élargissant le déterminant ci-dessus,

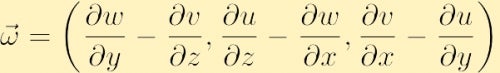
Un autre aspect important de la dynamique des fluides lié à la vorticité est la circulation. Contrairement à la vorticité qui est une propriété locale, définie en tout point de l’espace, la circulation est une propriété globale, définie en intégrant une propriété du fluide sur une courbe. En particulier, si vous choisissez un contour fermé et le désignez par la lettre C(t), la circulation autour de C(t), dans le sens antihoraire, est une grandeur scalaire notée avec,

est définie comme,

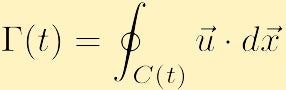
qui peut être fonction du temps, tout comme le contour fermé.

Prenons un moment pour expliquer ce que cela dit physiquement. En chaque point du contour (t), nous trouvons la composante de la vitesse tangente à la courbe et multiplions ce scalaire par une longueur infinitésimale; projeter la vitesse sur la tangente donnera nécessairement une grandeur entre la vitesse à cette position et zéro. Si la vitesse est tangente à la courbe, alors nous obtenons plus ou moins la vitesse de, si la vitesse est orthogonale à la courbe, nous obtenons zéro. Ensuite, nous intégrons cette quantité, une manière différente de dire en additionnant un nombre infini de choses, autour du contour pour que nous ajoutions la contribution de chaque point. À partir de là, nous vérifions que la circulation le long d’un contour C(t) est la quantité d’écoulement autour du contour (t); un résultat positif ou négatif correspond à une circulation dans le sens des aiguilles d’une montre ou dans le sens des aiguilles d’une montre, respectivement. Un cas extrême est celui où le champ de vitesse est partout perpendiculaire à la courbe C(t) et par conséquent il n’y a pas de circulation puisque le flux traverse toujours le contour et ne s’écoule jamais le long du contour. Pour obtenir une circulation non nulle, il doit y avoir une partie de la courbe où l’écoulement est le long du contour fermé.

Si le champ de vitesse est lisse et qu’il n’y a pas de singularités dans C(t), nous pouvons utiliser le théorème intégral de Stokes à partir du calcul vectoriel pour réécrire la circulation sous la forme suivante:

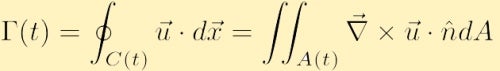
où A est l’aire contenue dans le contour C et λ est le vecteur normal unitaire de l’areaA.

Avant d’envisager cette nouvelle équation pour la circulation, il est utile de comprendre la signification physique du théorème de Stokes où le champ vectoriel est la vitesse. Dans la double intégrale ci-dessus, nous calculons la vorticité en chaque point du contour, puis résumons la vorticité sur tous ces points en A(t). Dans l’intégrale unique sur le contour fermé, nous calculons l’écoulement le long de la limite de la zone. Le théorème de Stokes stipule alors que ces quantités sont égales, et donc que s’il y a une vorticité moyenne dans une zone, ce qui doit alors signifier que la zone a un taux de rotation non nul, il doit donc y avoir une circulation nette le long du périmètre de cette limite.

À partir du Théorème de la Valeur Moyenne du calcul, nous pouvons remplacer l’intégrande dans l’intégrale double par une valeur moyenne, qui correspond à la composante moyenne de la vorticité orthogonale au plan dans lequel se trouve C(t). Ainsi, la deuxième interprétation de la circulation est qu’il s’agit de la vorticité moyenne multipliée par la surface contenue dans C(t). Au lieu de calculer la circulation sur le contour fermé C(t), nous pouvons calculer la vorticité moyenne normale à A(t) et la multiplier par l’aire à l’intérieur. Si l’on considère le cas particulier où la vorticité est partout constante, la circulation serait de l’ampleur de la vorticité multipliée par la zone qu’elle contient.

Un vortex ponctuel est un vortex qui n’a pas de surface, ce qui signifie que la vorticité n’est présente qu’en un seul point. Pour étudier les tourbillons ponctuels, nous supposerons d’abord que nous avons un flux incompressible 2D. (Les tourbillons ponctuels sont également parfois appelés tourbillons de ligne lorsqu’ils sont visualisés en 3D.)

Après quelques calculs, nous déterminons que le champ de vitesse généré par un tourbillon ponctuel, sous forme complexe, situé à z0 est donné par (où Gamma zéro est la circulation autour du tourbillon ponctuel, souvent appelée force du tourbillon ponctuel):

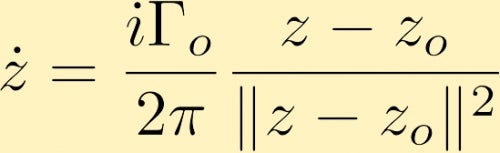
Le champ de vitesse généré par un tourbillon ponctuel peut provoquer le déplacement d’un autre tourbillon ponctuel . En voici quelques exemples: Les tourbillons à deux points, à la fois positifs et de magnitude égale, les tourbillons à deux points, tous deux positifs mais l’un a trois fois la force de l’autre et un tourbillon ponctuel est négatif avec deux fois la magnitude de l’autre qui est positif. Une autre possibilité est de considérer deux tourbillons ponctuels de même amplitude mais de signe opposé.

Ceci peut être étendu à n’importe quel nombre de tourbillons ponctuels, N. L’équation du mouvement sous forme complexe pour un tourbillon ponctuel alpha est donnée par:

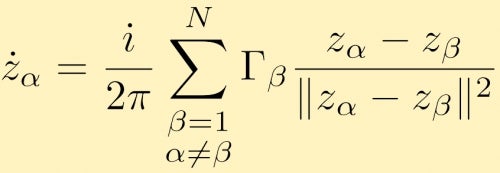
Regarder les interactions des tourbillons ponctuels est un problème très intéressant qui est difficile à faire analytiquement d’autant plus que le nombre de tourbillons ponctuels augmente. Les simulations numériques des interactions ponctuelles de vortex sont donc très courantes. Une application utile des simulations de grands tourbillons ponctuels est si vous regardez de grands groupes de tourbillons ponctuels qui simulent des tourbillons à aire finie. Voici les descriptions et les résultats de plusieurs simulations de vortex à grands points. Dans ce cas, nous avons deux grands groupes de tourbillons ponctuels de force égale fusionnant. Dans le cas suivant, nous commençons par un anneau de véracités ponctuelles groupées.

Pour trouver une équation pour l’évolution de la vorticité, nous commençons par l’équation de l’élan. Dans l’équation de moment, le terme advectif peut être réécrit comme suit,

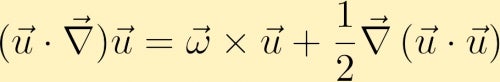
Nous calculons ensuite la boucle de l’équation de moment et à travers certaines identités de vecteurs, nous obtenons l’équation de vorticité:

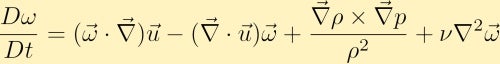
L’équation de vorticité montre comment la vorticité peut être générée dans un fluide. Sans perte de généralité, nous supposerons qu’au départ, nous n’avons que la vorticité dans la direction z. De là, nous pouvons voir comment chacun des quatre termes différents peut modifier la vorticité.

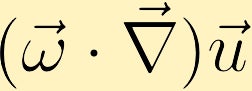
S’il y a un changement de vitesse avec la direction de la vorticité existante, la vorticité peut être générée.

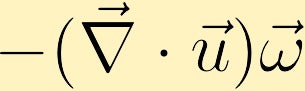
Si une parcelle de fluide se dilate et que la vorticité est positive, la vorticité de la parcelle de fluide diminuera et si la parcelle se contracte, la vorticité augmentera.

Les couches fluides de densité constante (isopycnales) veulent coïncider avec les couches de pression constante (isobares). Si ces couches ne coïncident pas, le fluide commence à tourner pour les aligner, ce qui génère une vorticité. (Dans l’exemple, nous commençons par une vorticité nulle.)

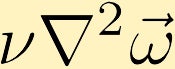
Les forces visqueuses provoquent la diffusion de la vorticité. (Dans l’exemple, nous commençons par un point de vorticité infinie au centre.)