a folyadékdinamika szerves része az örvényesség. Heurisztikusan méri a folyadékcsomag helyi forgását. A szilárd tárgyak esetében nem egy tárgy örvényességéről beszélünk, hanem annak szögsebességére utalunk. Ez a két fogalom összefügg, de a vorticitás hasznosabb, ha deformálódó forgó tárgyakat tárgyalunk, mint egy folyadék.

egy adott sebességmező örvényességét egy adott síkban úgy számítjuk ki, hogy kiválasztunk két ortogonális tengelyt az adott síkban, és hozzáadjuk az egyes tengelyek szögsebességét. Szilárd tárgyban vagy olyan folyadékban, amely szilárd tárgyként forog (találóan elnevezve szilárd test forgása), az örvényesség kétszerese a szögsebesség mivel minden tengely azonos sebességgel forog. Egy folyadékban azonban a két tengely nagyon eltérő sebességgel, sőt különböző irányokban is foroghat! Még az is lehetséges, hogy minden tengely foroghat, mégis a nettó örvény nulla (lásd irrotációs örvény).

Ha a folyadék mozgása szigorúan egy síkban való fekvésre korlátozódik, akkor az örvényvektor merőleges a síkra, és nem képes megváltoztatni az irányokat (vagy dőlni). Az örvényesség egyetlen aspektusa, amely megváltozhat, annak nagysága. Úgy gondolják, hogy ez az energiaátadás nagyobb méretekre kapcsolódik a Jupiter nagy vörös foltjának kialakulásához.

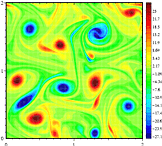
háromdimenziós folyadékmozgásban a vorticitási vektor háromdimenziós, mivel az egyes tengelyekkel párhuzamos komponensekkel rendelkezik, x, y és z: A z komponens párhuzamos a z tengellyel, és leírja az xy síkban a forgási sebességet. Ennek a kettősségnek köszönhető, hogy minőségi különbség van a viselkedésben a kétdimenziós turbulencia és a háromdimenziós turbulencia között. Az előbbiben az a tendencia figyelhető meg, hogy az örvények összetapadnak és nagyobb örvényeket alkotnak, míg az utóbbiban az örvények mozgása szétszakad, és az energia a legkisebb léptékig zuhan, ahol aztán szétszóródik.

matematikailag egy adott sebességmező örvényessége,

a sebességmező görbülete, amelyet általában görög omega betűvel jelölnek,

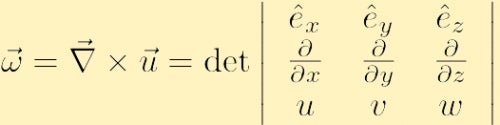
ahol a hagyományos Nabla szimbólumot használtuk a gradienshez:

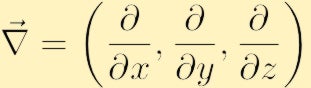
komponens formában a vorticitást a fenti determináns kibővítésével találjuk meg,

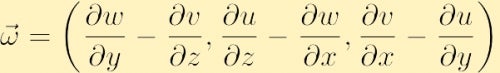
a folyadékdinamika másik fontos szempontja, amely az örvényességgel kapcsolatos, a keringés. Ellentétben az örvényességgel, amely a tér minden pontján meghatározott helyi tulajdonság, a keringés globális tulajdonság, amelyet a folyadék tulajdonságának egy görbére történő integrálásával határozunk meg. Különösen, ha bármilyen zárt kontúrt választasz, és C(t) betűvel jelölöd, a C(t) körüli keringés az óramutató járásával ellentétes irányban egy skaláris mennyiség, amelyet a következővel jelölünk:

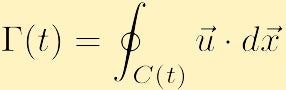
ami az idő függvénye lehet, csakúgy, mint a zárt kontúr.

szánjunk egy percet arra, hogy elmagyarázzuk, mit mond ez fizikailag. A kontúr(t) minden pontján megtaláljuk a sebességnek a görbét érintő összetevőjét, és megszorozzuk ezt a skalárt egy végtelen hosszúsággal; a sebességnek az érintőre vetítése szükségszerűen nagyságot ad az adott helyzetben lévő sebesség és a nulla között. Ha a sebesség érintő a görbe akkor kapunk plusz vagy mínusz a sebesség, ha a sebesség merőleges a görbe, kapunk nulla. Ezután integráljuk ezt a mennyiséget, a végtelen számú dolog összegzésének más módját a kontúr köré, hogy minden pontból hozzáadjuk a hozzájárulást. Ebből megállapítjuk, hogy a C(t) kontúr mentén a keringés a kontúr körüli áramlás mennyiségec (t); a pozitív vagy negatív eredmény megfelel a kontúrnak az óramutató járásával megegyező vagy az óramutató járásával megegyező irányban. Az egyik szélsőséges eset az, amikor a sebességmező mindenütt merőleges a C(t) görbére, következésképpen nincs keringés, mivel az áramlás mindig keresztezi a kontúrt, és soha nem áramlik a kontúr mentén. A nem nulla keringés eléréséhez a görbe egy részének kell lennie, ahol az áramlás a zárt kontúr mentén van.

Ha a sebességmező sima, és nincsenek szingularitások a C(t) – en belül, akkor használhatjuk Stokes integrál tételét a vektorszámításból, hogy átírjuk a keringést, mint,

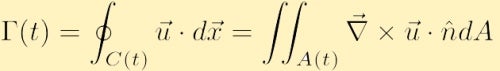
ahol A a kontúron belüli terület C, és az egység normál vektora a területnekaa.

mielőtt a keringés ezen új egyenletét szemlélnénk, hasznos megérteni a fizikai jelentését Stokes-tétel ahol a vektormező a sebesség. A fenti kettős integrálban kiszámítjuk az örvényességet a kontúr minden pontján, majd összefoglaljuk az örvényességet az a(t) összes pontján. A zárt kontúr feletti egyetlen integrálban kiszámítjuk az áramlást a terület határa mentén. Stokes tétele ezután kimondja, hogy ezek a mennyiségek egyenlőek, és így ha egy területen belül átlagos örvényesség van, ami azt jelenti, hogy a területnek nem nulla forgási sebessége van, akkor ennek a határnak a kerülete mentén nettó keringésnek kell lennie.

a számítás középérték-tételéből helyettesíthetjük a kettős integrál integrandusát egy átlagértékkel, amely megfelel a vorticitás átlagos komponensének, amely merőleges a síkra, amelyben C(t) fekszik. Így a keringés második értelmezése az, hogy az átlagos örvényesség szorozza meg a C(t) – ben található területet. Ahelyett, hogy kiszámítanánk a keringést a C(t) zárt kontúron, kiszámíthatjuk az átlagos örvénylést a(t) – re, és megszorozhatjuk azt a belső területtel. Ha figyelembe vesszük azt a különleges esetet, amikor az örvényesség mindenütt állandó, akkor a keringés az örvényesség nagysága lenne, szorozva a benne lévő területtel.

a pont örvény olyan örvény, amelynek nincs területe, ami azt jelenti, hogy az örvényesség csak egyetlen ponton van jelen. A pontörvények tanulmányozásához először azt feltételezzük, hogy van egy 2D összenyomhatatlan áramlásunk. (A pontörvényeket néha vonalörvényeknek is nevezik, ha 3D-ben nézzük.)

néhány számítás után megállapítjuk, hogy a z0-nál elhelyezkedő pont örvény által generált sebességmezőt (ahol a Gamma nulla a pont örvény körüli keringés, amelyet gyakran a pont örvény erősségének neveznek):

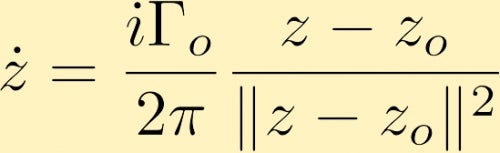
az egyik pont örvény által generált sebességmező egy másik pont örvény mozgását okozhatja. Íme néhány példa erre: A két pont örvény, mind pozitív, mind egyenlő nagyságrendű, a két pont örvény, mindkettő pozitív, de az egyik háromszorosa a másik erősségének ,az egyik pont örvény negatív, a másik kétszerese pedig pozitív. Egy másik lehetőség két azonos nagyságú, de ellentétes előjelű pont örvény figyelembevétele.

Ez tetszőleges számú pontörvényre kiterjeszthető, N. a mozgás egyenlete komplex formában egy pontörvényes alfa számára:

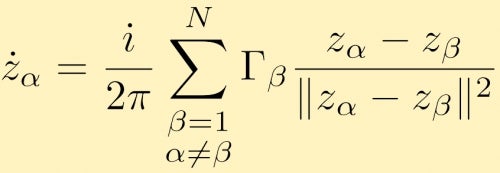
a pontörvények kölcsönhatásainak vizsgálata nagyon érdekes probléma, amelyet analitikusan nehéz megtenni, különösen a pontörvények számának növekedésével. A pont örvény kölcsönhatásainak numerikus szimulációja tehát nagyon gyakori. A nagy pontörvényszimulációk egyik hasznos alkalmazása, ha nagy pontörvények klasztereit vizsgáljuk, amelyek véges területű örvényeket szimulálnak. Itt vannak leírások és az eredmények több nagy pont örvény szimulációk. Ebben az esetben két nagy, azonos erősségű pontörvénycsoport van összeolvadva. A következő esetben kezdjük egy gyűrű fürtözött pont veracities.

a vorticitás evolúciójának egyenletének megtalálásához a momentumegyenlettel kezdjük. A momentum egyenletben az advektív kifejezés a következőképpen írható át,

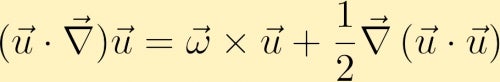
ezután kiszámítjuk a momentum egyenlet görbületét, és néhány vektorazonosságon keresztül megkapjuk a vorticitási egyenletet:

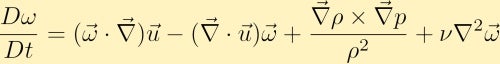
a vorticitási egyenlet megmutatja, hogyan generálható a vorticitás egy folyadékban. Az általánosság elvesztése nélkül feltételezzük, hogy kezdetben csak Z irányú örvényünk van. Ebből láthatjuk, hogy a négy különböző kifejezés hogyan változtathatja meg az örvényt.

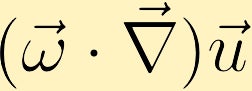
Ha a sebesség megváltozik a meglévő örvényesség irányával, örvényesség generálható.

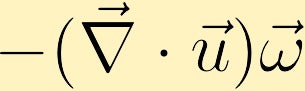
Ha egy folyékony csomag tágul, és az örvényesség pozitív, akkor a folyékony csomag örvényessége csökken, ha a csomag összehúzódik, az örvényesség növekszik.

az állandó sűrűségű folyadékrétegek (izopiknálok) egybeesnek az állandó nyomású rétegekkel (izobárok). Ha ezek a rétegek nem esnek egybe, akkor a folyadék forogni kezd, hogy sorba álljon, ami örvényességet okoz. (A példában nulla örvényléssel kezdjük.)

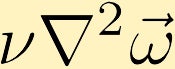
a viszkózus erők okozzák a vorticitás diffúzióját. (A példában a végtelen örvényesség pontjával kezdjük a központban.)