május 31-én, 1832-ben, egy francia republikánus forradalmár, az úgynevezett Multinvariste Galois halt meg egy lövéstől. 20 éves volt. Előző este, saját halálától tartva, Galois sok levelet írt, frenetikusan firkálva:”nincs időm; nincs időm”. Egy levél történelmi okokból különösen értékes. Ebben a levélben Galois azt állítja, hogy valóban kiváltotta a forradalmat. Nem politikai. De egy matematikai.

a Galois által kezdeményezett forradalom nagyobbnak és mélyebbnek bizonyult, mint amit el tudott volna képzelni! A táj a matematika már mélyen érintette Galois víziója, mint az utódai emelkedett, és átvette a matematikai világban. Ez az utód most mindenütt jelen van, és határtalan földeket szabályoz. Tiszta algebra néven fut.

hogy még egy kicsit romantikusabbá tegyük Galois drámai életének történetét, itt van egy absztrakt egy dokumentumfilmről, amelyet az algebráról készítettem:

határozottan az! De a matematikai forradalma nem ment simán. Mint minden forradalmi vezető, először a legnagyobb nehézségekkel küzdött. Nem elképzelni a forradalmat. De meggyőzni másokat, hogy csatlakozzanak hozzá a matematika játékváltoztató megközelítéséhez. Amikor Galois még életben volt, forradalmi ötleteit a Francia Tudományos Akadémia többször elutasította … mert az akkori legjobb francia matematikusok, mint Sim ons Denis Poisson, egyszerűen nem tudták megszerezni! Részben azért, mert Galois ‘ olvashatatlan kézírás jelenik meg a jobb oldalon …

1843-ban, 10 évvel Galois halála után, végül egy zseniális francia matematikus, Joseph Liouville sikerült megragadnia Galois néhány ötletét. További 3 év munka után Liouville cikket tett közzé, hogy elmagyarázza őket. De Liouville cikke még mindig túl erőltetett más matematikusok élvezni és megérteni. További 24 évbe telt, mire egy francia matematikus elég kiemelkedő volt ahhoz, hogy jobban megértse Galois-t, és ötleteit lágyabbá tegye. Ez a kiemelkedő matematikus Camille Jordan. Valójában Jordan 1870-es könyve a Galois-elméletről olyan jól megírt volt, hogy Felix Klein német matematikus ugyanolyan olvashatónak találta, mint egy német könyv!

Ez határozottan egy hatalmas lökést. De további 82 évbe telik, amíg a nagy osztrák matematikus, Emil Artin 1942-ben végre megadja a Galois-elmélet modern formáját. Artin sok kreditet érdemel. Míg Galois volt a látnok, aki előre látta ezt a forradalmat, Artin, sok értelemben, az, aki ténylegesen vállalta a forradalom és felborult a matematika. Hála Artin, és néhány más, ma, a Galois-elmélet vált elkerülhetetlen sarokköve a kutatás a matematikában, rengeteg meglepő és elképesztő eredményeket (mint Wiles ‘proof of Fermat’ s last theorem), valamint egy hatalmas tározó nyitott kérdések és rejtélyek!

mezők a tiszta algebrában

a Galois-elmélet a számok szimmetriáiról szól. De mielőtt odaérnék, be kell mutatnom, hogy felfegyverezzem azzal, hogy elárulok egy titkot a számokról. És biztos vagyok benne, hogy hallottál róla! Valóban, vissza a középiskolába, valószínűleg azt tanították, hogy soha ne hagyjon gyökereket a nevezőkben.

úgy értem, hogy $1 / (\sqrt{2}-1)$ nem volt helyes válasz. Tudna segíteni megszabadulni a 2 négyzetgyökétől a nevezőben?

Hehe … megtanítottak fel-le szorozni a nevező konjugátumával. Ezt a konjugátumot úgy kapjuk meg, hogy $ – $ -t $ + $ -ra (vagy fordítva) cseréljük a nevezőben:

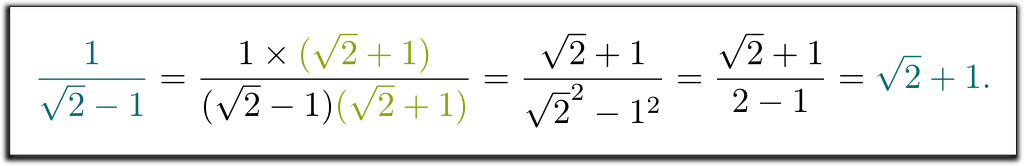
tudom! A $1/(\sqrt{2}-1)$ bonyolult kifejezés ugyanazt a számot jelenti, mint a $\sqrt{2}+1$. Ez megmagyarázza, hogy a tanáraink miért akarták, hogy az eredményeket inkább az egyik, mint a másik módon írjuk le: amikor minden ugyanúgy van írva, a vizsgákat sokkal könnyebb kijavítani!

de mi a helyzet $1/(\sqrt{2}-1)$? Meg tudsz szabadulni a nevező gyökerétől? Meg lehet egyáltalán csinálni?

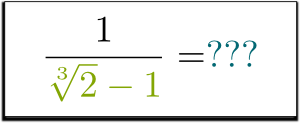
tudom!

mondd meg!

szerencséd van?

Hehe … érdekes módon a $ \ sqrt{2}-1$ bármely ereje felírható $ \ sqrt{2}$hatványainak összegeként. Valójában csak a termékeket kell terjesztenie:

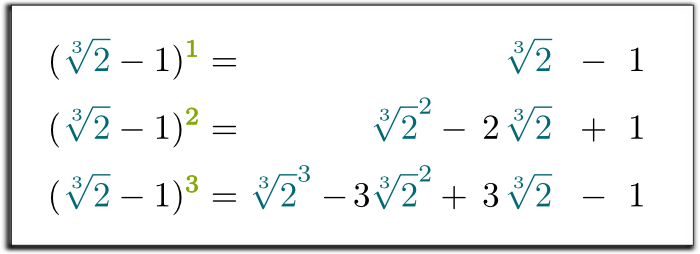
Igen, ez az! Ezzel a helyettesítéssel a harmadik egyenletben megmutattuk, hogy a $ \ sqrt{2}-1$ három első hatványa egy racionális szám összegeként írható, $\sqrt{2}$ és $\sqrt{2}^2$!

tehát most 3 egyenlet van, 2 gyökér kifejezéssel meg akarunk szabadulni! Így kombinálhatjuk az egyenleteket, hogy eltávolítsuk az összes gyökér kifejezést a jobb oldalon!

szorozzuk meg a 2 első sort 3-mal, és adjuk össze mind a 3 egyenletet:

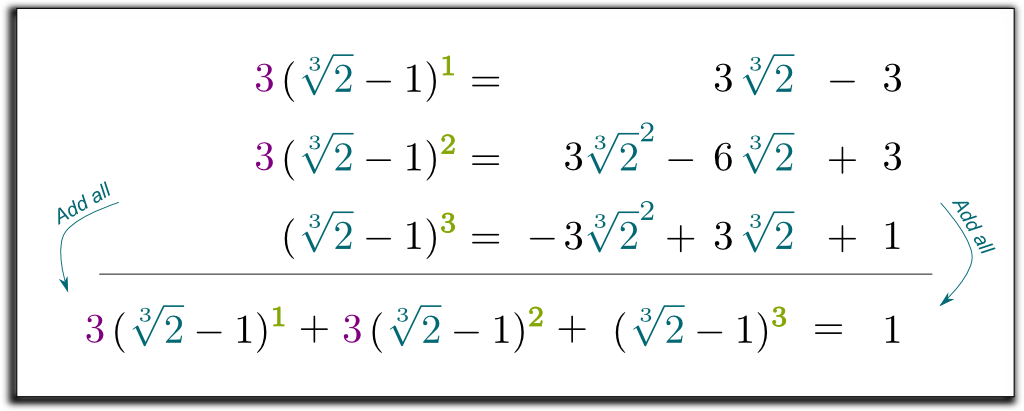
Hehe… a klassz dolog az, hogy a kapott bal kifejezést most $\sqrt{2}-1$faktorizálhatjuk! Hadd ugorjak át néhány unalmas számítást … és érjem el az eredményt $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \ sqrt{2} + 1)$ $= 1$. Tehát, hogy megszabaduljunk a nevező gyökereitől, fel-le szaporodhatunk $\sqrt{2}^2 + \sqrt{2} + 1$ – val! Végül a következő meglepő és gyönyörű képletet kapjuk:

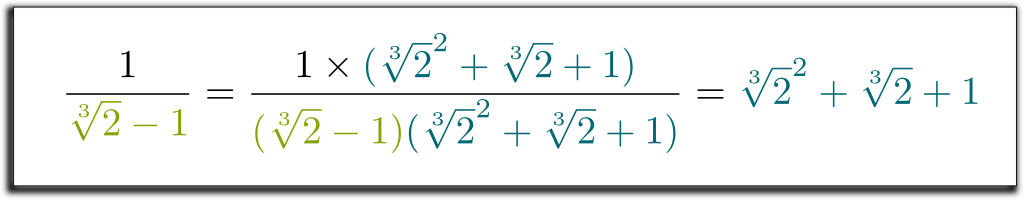
tudom! De ami még rendesebb, hogy az általunk alkalmazott módszer nagyon általános! Hasonló technikával most eltávolíthatjuk az összes gyököt a nevezőkből!

Galois számára nem az volt különösen érdekes, hogy egy módszer lehetővé tette a gyökök eltávolítását a nevezőkből. De inkább, hogy bármely szám, amelynek nevezőjében gyökök vannak, megegyezett a tetején lévő gyökökkel. Ez azt jelentette, hogy a tetején lévő radikálisokkal rendelkező számok Osztás szerint stabilak voltak.

gyakori a $ \ mathbb Q{2}]$ a számok halmaza, amelyet $ \ sqrt{2}$hatványainak összegeként lehet írni. Mivel a $ \ sqrt{2}^3 = 2$ racionális szám, a $\sqrt{2}$ hatványainak összege valójában a $a\sqrt{2}^2 + b\sqrt{2} + c$szabványos formában írható. Most, ha összeadunk, kivonunk vagy megszorozunk két ilyen számot, akkor nem nehéz belátni, hogy olyan számokat kapunk, amelyek továbbra is a szokásos formában helyezhetők el $a\sqrt{2}^2 + b\sqrt{2} + c$. Ráadásul, amit most bemutattunk itt, az az, hogy az összes szám inverze $a\sqrt{2}^2 + b\sqrt{2} + c$ szabványos formában is írható. Ez azt mutatja, hogy a $\mathbb Q{2}]$ számok összeadása, kivonása, szorzása és osztása olyan számot eredményez, amely standard formában írható… és így a $\mathbb Q{2}]$ – hoz tartozik. Tiszta algebrai értelemben a $ \ mathbb Q{2}]$ tehát stabil a négy klasszikus aritmetikai művelettel. Ezért nevezzük ezt mezőnek.

Mezőbővítmények geometriája

a mező, amelyet a legjobban ismer, valószínűleg a racionális számok $\mathbb Q$ halmaza. További példák a mezőkre a valós számok $\mathbb R$ halmaza és a komplex számok $\mathbb C$ halmaza. És most van $ \ mathbb Q{2}]$is. Mivel a $ \ mathbb Q{2}]$ egy mező, amely tartalmazza a $\mathbb Q$ mezőt, azt mondjuk, hogy a $ \ mathbb Q{2}] / \mathbb Q$ egy mező kiterjesztés.

az a tény, hogy $\mathbb Q{2}] / \mathbb Q$ egy mező kiterjesztés, nagyon természetes kapcsolatot eredményez a két mező között. Nevezetesen, $ \ mathbb Q{2}]$ vektortérnek tekinthető, ahol $ \ mathbb Q$ A skaláris mező. Különösen az a tény, hogy a $\mathbb Q{2}]$ bármely szám felírható $a \ sqrt{2}^2 + b\sqrt{2} + c$ azt jelenti, hogy $(1, \sqrt{2}, \sqrt{2}^2)$ a $\mathbb Q{2}]$ alapját képezi $\mathbb Q$-vektortérként. Ez azt jelenti, hogy geometriailag 3 dimenziós térként ábrázolhatjuk!

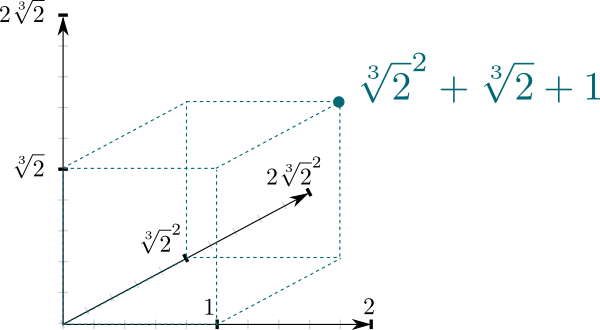
a fenti vektortér dimenziója a mezőbővítmények érdekes tulajdonsága. Ez az úgynevezett fok, és általában $\big{2}] : \mathbb Q\big] = 3$ például.

Igen! Valójában nagyon könnyű létrehozni ennek a mezőnek a kiterjesztését: csak adjon hozzá néhány radikális számot, amely nem tartozik a $\mathbb Q{2}]$ – hoz!

Igen! Ez létrehozná a $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$mezőt. Ez a mező tartalmazza az összes számot, amelyek $\sqrt{2}$ és $\sqrt{2}$termékek és összegek. Ezek formája $a \ sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ F \sqrt{2}$. Van ötlete, hogy mi a fok $ \ big{2}, \ sqrt{2}]: \ mathbb Q{2}] \ big]$?

Igen! Valóban, van $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} \sqrt{2} $ + $ F \sqrt{2} $ = $ (a \sqrt{2}^2 + b\sqrt{2}+c) $ + $ (d\sqrt{2}^2 + e\sqrt{2} + f) \sqrt{2}$. Így tetszőleges számú $ \ mathbb Q{2},\sqrt{2}]$ írható $a+B\sqrt{2}$, ahol $a$ és $B$ a $\mathbb Q{2}]$ – hoz tartoznak. Így a $\mathbb Q{2}]$ 2 skalárja meghatároz egy számot a $\mathbb Q{2},\sqrt{2}]$ – ban. Ez azt jelenti, hogy a $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ mező kiterjesztés mértéke 2. Valójában megvan a Chasles reláció $ \ big{2}, \ sqrt{2}]: \ mathbb Q \ big] $ = $ \ big{2}, \ sqrt{2}] : \mathbb Q{2}] \ nagy] \ nagy{2}]: \mathbb Q \nagy] $ = $ 2 \ szorozva 3 = 6$.

ez jobb, mint ez! Bármely véges fokú mező kiterjesztést, az úgynevezett véges mező kiterjesztést egyetlen szám fedi le. Például $ \ mathbb Q{2}, \ sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, ami azt jelenti, hogy minden szám, amely $\sqrt{2}$ és $\sqrt{2}$ hatványainak összege, egyben $\sqrt{2} + \sqrt{2}$hatványainak összege is. Hát nem meglepően király?

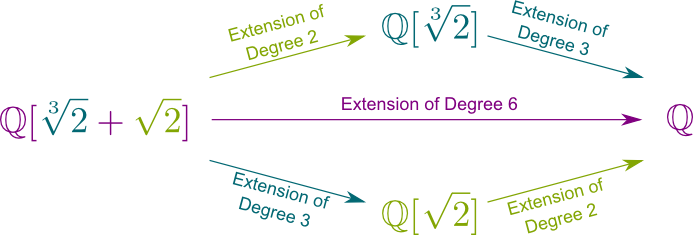
általánosabban, a $\mathbb Q$ bármely véges mezőbővítménye $\mathbb Q$ – ra írható, néhány $x$ – val, amely hozzáadódik a $\mathbb Q$ – hoz.

Igen. Ez a helyzet a mező kiterjesztés $ \ mathbb R/ \ mathbb Q$. És, így a legfontosabb mező kiterjesztése Galois elmélet! Ez a mező kiterjesztés $ \ bar {\mathbb Q} / \mathbb Q$, ahol $\bar {\mathbb Q}$ az algebrai számok halmaza. Ezek mind megoldások az űrlap polinom egyenleteire $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $ + $ a_0 = 0$. Például, $ \ sqrt{2}$ egy algebrai szám, mert megoldás $x^4 – 2x = 0$. Így a $ \ bar {\mathbb Q}$ A $\mathbb Q$összes véges mezőbővítményének mezőbővítése.

konjugált számok

már majdnem ott vagyunk! Szükségünk van egy utolsó kitérőre a polinom egyenleteken keresztül.

pontosan! Galois észrevette, hogy néhány egyenlet egyszerűsíthető. Például $x^4-2x=0$ faktorizálható $x(x^3-2)=0$, ami megfelel $x=0$ vagy $x^3-2=0$. Tehát a $x^4-2x=0$ egyenlet csökkenthető $x=0$ és $x^3-2=0$egyenletekre. És valójában ez a csökkenés nagyon hasonlít ahhoz, ahogyan a 35-ös számokat 5-re és 7-re lehet csökkenteni, mert $5 \szorozva 7 = 35$. Az egyenletek és az egész számok közötti hasonlóság olyan erős, hogy még a polinomok euklideszi felosztását is meg tudjuk csinálni, ahogy a számoknál is megtanultad! A jobb oldalon egy példa egy ilyen megosztásra (ne aggódjon, ha nem érti, ez nem lesz fontos a folytatás szempontjából).

pontosan! Ezeket redukálhatatlan polinomegyenleteknek nevezzük. A $x^3-2=0$ egyenlet az irreducibilis polinom egyenlet példája.

Igen! De döntő fontosságú, hogy Galois a racionális együtthatókkal rendelkező egyenletekre akart összpontosítani. Vagy inkább az alapmezőhöz tartozó együtthatókkal rendelkező polinomok. Tehát arra gondoltam, hogy a $ \ mathbb Q$ mint alapmező, $x^3-2=0$ irreducibilis.

tekintsük $x^2 – 2x -1=0$, hogy néhány nyomokat. Ez az egyenlet bizonyítható, hogy irreducibilis. Emlékszel, hogyan kell megoldani?

ha $b^2-4ac \ geq 0$, igen.

pontosan! Tehát a $x^2 + 2x -1=0 $ redukálhatatlan polinom egyenletnek két megoldása van: $1+ \ sqrt{2}$ és $1- \ sqrt{2}$ … van valami megjegyzés?

Bingo! Ez Galois legfontosabb felfedezése. Általánosabban, Galois hívott konjugálja az összes megoldást egy redukálhatatlan polinomegyenletre. És ahogy el tudod képzelni, ezek elengedhetetlenek a gyökök eltávolításához a nevezőkből!

az első dolog, amit észre kell venni, hogy ha $x_1$, $x_2$,…, $x_n$ egy polinom irreducibilis egyenlet összes megoldása $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ racionális együtthatókkal, akkor ez a polinom irreducibilis egyenlet valóban átírható $a_n(x-x_1)(x-x_2)…(x-x x_n)=0$. Az állandó kifejezések azonosítása ekkor $x_1 x_2 … x_n $=$ (-1)^n a_0/a_n$értéket eredményez. Tehát döntő fontosságú, hogy a konjugált számok szorzata a racionális szám $(-1)^n a_0/a_n$, amely nem nulla (bizonyítsd be!).

itt egy kis vicc, hogy szem előtt tartsuk a konjugátumok közötti erős kapcsolatot:

Vegyünk egy frakciót $1 / x_1$, ahol $x_1$ egy bonyolult kifejezés gyökökkel. Ha fel-le szorozzuk a $x_2$, …, $x_n$ konjugátumokkal $x_1$ – ból, akkor $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$-t kapunk, amelynek nincs gyöke a nevezőben, mivel megállapítottuk, hogy $a_0$ az alapmező nem nulla száma!

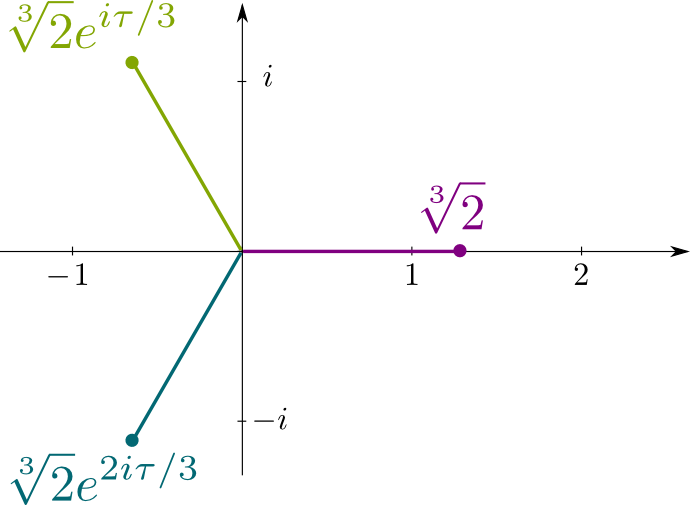
emlékezzünk arra, hogy $x^3-2=0$ az irreducibilis polinom egyenlet $\sqrt{2}$ a megoldása. Tehát konjugátumai az egyenlet további megoldásai, amelyek a $\sqrt{2}j$ és $\sqrt{2}j^2$ Komplex számok, ahol $j= e^{i\tau/3}$ a $\tau = 2\pi$ a kör kerületének sugara szerinti aránya. A következő ábra mutatja a konjugált megoldások helyét ebben a komplex síkban:

Galois kétértelműsége

végül eljutunk Galois legfontosabb betekintéséhez!

konjugátumok tökéletesen permutálhatók. Ez azt jelenti, hogy ha szisztematikusan megváltoztatja a $ \ sqrt{2}$ konjugátumát $-\sqrt{2}$, akkor az egyenlőségek továbbra is fennállnak. Például, mivel $1/(\sqrt{2}-1) = \sqrt{2}+1$ volt, egyértelműen elmondhatom, hogy $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! Hasonlóképpen, a következő lenyűgöző következménnyel rendelkezünk:

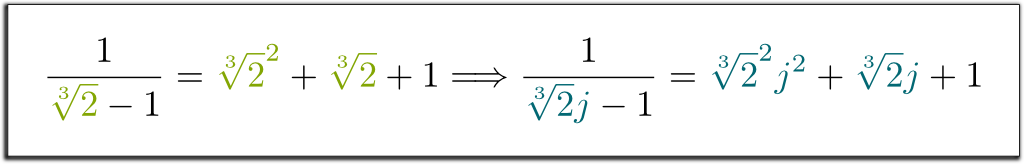
Hehe … hadd idézzem fel először, hogy a véges mezőket egyetlen elem fedi le. Tehát, ha az alapmező $ \ mathbb Q$, bármely véges mező írható $ \ mathbb Q$ néhány jobbra $ x_1$. Most fontolja meg $x^n + a_{n-1}x^{n-1} $ + $ … + a_1 x + a_0 = 0$ a redukálhatatlan polinom egyenlet $x_1$ a megoldás. Ezután mi határozza meg $ \ mathbb Q$ A $ \ mathbb Q$ – vektor tér által átfogott $x_1$, $x_1^2$, …, $x_1^{n-1}$, A $x_1$ nagyobb hatalmainak egyszerűsítésével az algebrai szabálynak megfelelően $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

pontosan! Alapvető fontosságú, hogy ezek a $\mathbb Q $ algebrai szabályok nem igazán függenek a $x_1$ jellegétől; csak az irreducibilis polinomtól függenek $x_1$ a megoldás! Ezért a $\mathbb Q$ szabályai megegyeznek a $\mathbb Q$, …, $\mathbb Q$ szabályaival, ahol a $x_1$ helyébe az egyik konjugátuma $x_2$, …, $x_n$lép. A $\mathbb Q{2}]$ és a $\mathbb Q{2} j]$ mezők pontosan ugyanazon szabályok szerint működnek. Ezért a konjugátumok tökéletesen átjárhatók! Azt mondjuk, hogy a $\mathbb Q{2}]$ és $\mathbb Q{2} j]$ mezők izomorfak, és hogy a $\sqrt{2}$ helyettesítése $\sqrt{2}j$ egy izomorfizmus $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

nagyon hasonló (de erősebb) módon, hogy a 2. dimenzió két vektortere többé-kevésbé azonos! Ennek szörnyű következménye van. Ez azt jelenti, hogy algebrai szempontból értelmetlen különbséget tenni egy szám és bármely konjugátuma között (mindaddig, amíg szisztematikusan helyettesítjük a számot a konjugátumával)! Tehát például a $ \ sqrt{2}$ és a $-\sqrt{2}$ algebrailag nem különböztethetők meg! Ezt szem előtt tartva, itt van egy másik vicc, amivel előálltam:

egyáltalán nem! A két szám közötti bármilyen megkülönböztetésnek az algebrán kívül más matematikát is magában kell foglalnia, például a rendviszonyokat vagy a topológiát. Úgy értem, hogy például a $\sqrt{2} > 0$ reláció különbséget tesz a $\sqrt{2}$ által $-\sqrt{2}$ között, de ez azért van, mert magában foglal egy megbízási relációt. De ha a polinom egyenlőségekre korlátozódunk, akkor egyáltalán nincs különbség $\sqrt{2}$ és $-\sqrt{2}$között. Hasonlóképpen,$ i $és$- i$, a$ x^2+1=0 $ irreducibilis polinom egyenlet megoldásai szintén algebrailag nem különböztethetők meg. Mégis, önkényesen $i$ – nak hívjuk őket. Ezért Galois elméletét a kétértelműség elméletének nevezte. Ma a $-1$ hagyományos négyzetgyökének a $i$ és $-i$ közötti választásának kétértelműségét inkább $i$ és $-i$közötti szimmetriának nevezzük.

Galois csoportok

Galois különösen összpontosított mező kiterjesztések, amelyek stabilak a konjugáció. Az ilyen stabil mezőbővítményeket ma Galois kiterjesztéseknek nevezik. Tehát, ha $x_1$ egy Galois kiterjesztéshez tartozik, akkor ez a Galois kiterjesztés tartalmazza az összes konjugátumát $x_2$,…, $x_n$.

a Galois-kiterjesztések felépítésének egyszerű módja az, hogy az irreducibilis polinom egyenlet megoldásaival átfogott mezőt vesszük. Például, ha $x_1$,…, $x_n$ a $\mathbb Q$ alapmező konjugátumai, akkor $ \ mathbb Q / \ mathbb Q$ egy Galois kiterjesztés. Az így felépített mezőket felosztó mezőknek nevezzük.

például a $x^3-2=0$ egyenlet hasító mezője a Galois kiterjesztés $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ A megoldásai által átfogva.

ha a$ x_1 $ átfogja a Galois kiterjesztést, akkor a konjugátumai is. Így $ \ mathbb Q = \ mathbb Q = $ … $ = \ mathbb Q$ = $ \ mathbb Q$. Így a $\mathbb Q$ és $\mathbb Q$ közötti izomorfizmus, amely abból áll, hogy mindig $x_1$ – t $x_2$ – ra cserélünk, valójában egy izomorfizmus $\mathbb Q$ és önmaga között! Ezt nevezzük automorfizmusnak. A $\mathbb Q/\mathbb Q$ Galois kiterjesztés automorfizmusai alkotják a $gal(\mathbb Q/\mathbb Q)$Galois csoportot.

most, döntő fontosságú, ha $ \ mathbb Q = \ mathbb Q$, akkor a Galois kiterjesztés $\mathbb Q/ \mathbb Q$ összes automorfizmusa $x_1$ permutációja az egyik konjugátumával! Különösen azt látjuk itt, hogy egy Galois-csoport kardinalitása megegyezik a Galois-kiterjesztés mértékével.

persze! Észrevehetjük, hogy $ \ mathbb Q = \ mathbb Q$ és $ \ mathbb Q = \ mathbb Q$, ami azt jelenti, hogy $i$ és $ \ sqrt{2}$ mindegyik átfogja az irreducibilis polinom egyenlet hasító mezőit, amelyekre megoldást jelentenek. Így a $ \ mathbb Q / \ mathbb Q$ és a $ \ mathbb Q / \ mathbb Q$ egyaránt Galois kiterjesztések. Ezért automorfizmusuk abból áll, hogy a $i$- t helyettesítik az egyik konjugátumával, $i$ vagy $- i$, és a $\sqrt{2}$ helyett $\sqrt{2}$ vagy $ – \sqrt{2}$. Az első esetekben nem változtatunk semmit számokra, ami megfelel a nulla szimmetriának. A második esetek axiális szimmetriaként jeleníthetők meg, amint az az alábbi ábrán látható:

hát nem csodálatos?

persze! Térjünk át a hasító mezőre $ \ mathbb Q{2}, \ sqrt{2}j, \ sqrt{2}j^2]$ of $x^3-2=0$. De mielőtt továbbmennénk, vegyük észre, hogy $ \ mathbb Q{2}, \ sqrt{2}j, \sqrt{2}j^2] = \ mathbb Q{2}, j]$.

mindössze annyit kell bizonyítanunk, hogy az egyik mező összes generátora a másikhoz tartozik. Kezdjük azzal, hogy bebizonyítjuk, hogy az utóbbi generátorai, a $\sqrt{2}$ és a $j$ az előbbihez tartoznak. Ez nyilvánvaló a $ \ sqrt{2}$esetében. Most, $j = (\sqrt{2} j) / \sqrt{2}$, így $j$ az előző mezőhöz is tartozik. Ez azt bizonyítja, hogy a $ \ mathbb Q{2}, j]$ összes eleme a $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$ – hoz tartozik. Kölcsönösen egyértelmű, hogy az előző mező összes generátora, $ \ sqrt{2}$, $\sqrt{2}j$ és $\sqrt{2}j^2$, az utóbbi generátorainak termékei. Így mindkét mező egyenlő. És különösen, $ \ mathbb Q{2}, j]/ \ mathbb Q$ egy Galois kiterjesztés.

Hehe … hogy megértsük a $\mathbb Q{2}]$ szimmetriáit, tovább kell mennünk a Galois-csoportok tanulmányozásában…

Galois-Levelezés

a Galois-csoportokkal az a baj, hogy rendkívül nagyok és bonyolultak lehetnek. Ez különösen igaz a végtelen csoport $Gal (\bar {\mathbb Q}/ \ mathbb Q)$. Ilyen hatalmas és összetett csoportok elfogására Galois briliáns ötlete támadt, hogy ezeket kisebb darabokra bontsa.

meglepő módon Galois rájött, hogy a Galois-csoportokat szimmetriák alcsoportjaira lehet bontani, ha csak azokat nézzük, amelyek néhány almezőt változatlanul hagynak. Például a $ \ mathbb Q$ A $\mathbb Q{2},j]$ almezője, mivel az előbbi tetszőleges száma az utóbbihoz tartozik. Így a $\mathbb Q{2},j]$ szimmetriái,amelyek semmit sem változtatnak $\mathbb Q$ – ra, a $\mathbb Q{2}, j]/\mathbb Q$Galois-csoportjának alcsoportját alkotják. Ezek a szimmetriák alkotják a Galois csoportot $Gal (\mathbb Q{2},j]/ \ mathbb Q)$.

tudom! Szeretem vizualizálni ezeket a szimmetriákat,mint a $\mathbb Q{2},j]$ csatlakoztatásának módját a $\mathbb Q$ – ra. Itt van egy leképezett kép a “dugulás”:

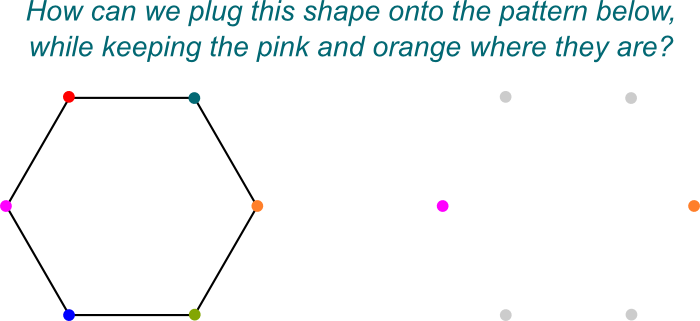
pontosan! És ez egyszerűen azért van, mert a $ \ mathbb Q{2}, j]$ A $\mathbb Q$ Galois kiterjesztése, amely maga is a $\mathbb Q$mező kiterjesztése.

és még több! Galois megmutatta, hogy a Galois kiterjesztések összes alcsoportját így kapjuk meg! Pontosabban,bármely $K$ mező leképezése a $\mathbb Q{2}, j]$ Galois kiterjesztés és a $\mathbb Q$ alapmező között a $Gal(\mathbb Q{2}, j] / K)$ Galois csoporthoz bijektív. Ezt a tényt Galois levelezésnek hívják! Ez a levelezés vázlatosan jelenik meg az alábbiakban egy Galois kiterjesztés $\mathbb Q/\mathbb Q$.

ahelyett, hogy ezt a csoportot közvetlenül leírnánk, összpontosítsunk a $Gal(\mathbb Q{2}, j]/\mathbb Q)$alcsoportjára. Egyértelmű, hogy a $ \ sqrt{2}$ átfogja a $\mathbb Q{2},j]$ értéket, amikor hozzáadják a $\mathbb Q$ – hoz. Így a $ \ mathbb Q{2}, j]/ \ mathbb Q$ egy Galois kiterjesztés, amely a $\sqrt{2}$. Ezért egy korábban látott tétel felhasználásával tudjuk, hogy ennek a Galois-kiterjesztésnek az összes automorfizmusa abból áll, hogy a $\sqrt{2}$ – t felváltja 3 konjugátumának egyikével (maga, $\sqrt{2} j$ és $\sqrt{2} j^2$)!

most folytathatnám a $Gal(\mathbb Q{2}, j]/\mathbb Q)$ más darabjainak tanulmányozását, mint például a Galois alcsoport $Gal(\mathbb Q{2},j]/\mathbb Q{2}])$. De én inkább használni egy másik Galois’ erős tételek. Nevezetesen bebizonyította, hogy ha a $ \ mathbb Q / \ mathbb Q$ emellett maga a Galois kiterjesztés is, akkor a $gal(\mathbb Q{2}, j]/\mathbb Q)$ alcsoport normális.

így a $\mathbb Q{2},j]/\mathbb Q$ Galois-csoportja hányados lehet ezzel az alcsoporttal, és a hányadoscsoport ekkor egyenlő $Gal(\mathbb Q/\mathbb Q)$ – val. Mégis, a $ \ mathbb Q / \ mathbb Q$ valóban egy Galois kiterjesztés, amelyet $j$ ölel fel, amelynek konjugátuma $j^2$. Így a $Gal (\mathbb Q/ \ mathbb Q)$ abból áll, hogy a $j$ – T $j$ – ként hagyja, vagy $j^2$ – ra cseréli.

a $Gal(\mathbb Q{2},j]/\mathbb Q)$ összes szimmetriáját levezethetjük a $Gal(\mathbb Q{2},j] / \mathbb Q)$ és $Gal(\mathbb Q/\mathbb Q)$kombinálásával. Ezeket a szimmetriákat úgy tudjuk megjeleníteni, hogy megrajzoljuk, hogyan befolyásolják a három átfogó konjugátumunkat $\sqrt{2}$, $\sqrt{2}j$ és $\sqrt{2}j^2$:

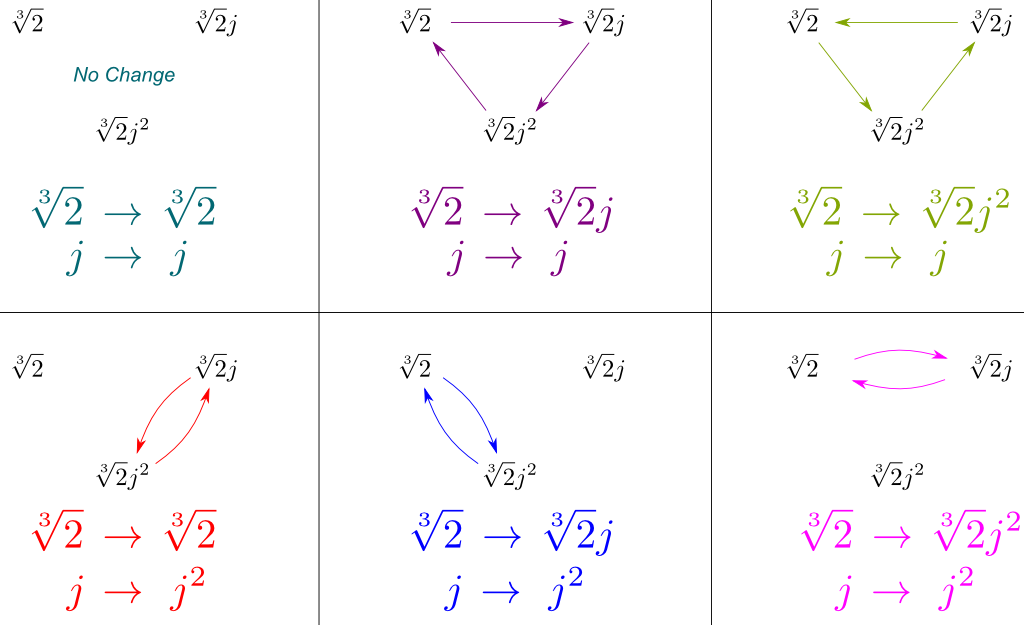
a fenti ábra A $Gal(\mathbb Q{2}, j]/\mathbb Q)$összes szimmetriáját tartalmazza. Meglepő módon ezek a szimmetriák megfelelnek a jól ismert szimmetriacsoportnak.

hagyom, hogy Marcus du Sautoy bemutassa neked:

tehát a szimmetriák itt olyanok, mint egy tengeri csillag vagy mint egy háromszög?

igen, valóban! A háromszög ezen szimmetriacsoportját $D_3$ – nak nevezzük, és megegyezik a $s_3$ 3 elem permutációinak csoportjával. Ez a következő képlethez vezet, amelyet olyan szépnek találtam, hogy úgy döntöttem, hogy bekeretezem!

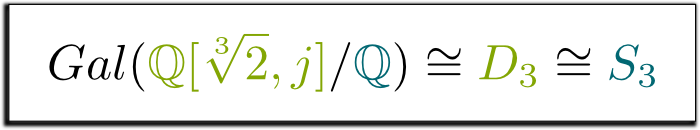
zárjuk le

sok szempontból Galois-t a modern algebra atyjának kell tekinteni. Legfontosabb meglátása az volt, hogy a matematikát a működési szabályok szögén keresztül vizsgálja, és ez arra késztette, hogy meglepő és éleslátó kétértelműségeket vagy szimmetriákat tárjon fel a számok között. Algebrai szempontból az olyan számok, mint $ \ sqrt{2}$, $\sqrt{2}j$ és $\sqrt{2}j^2$ valóban tökéletesen szimmetrikusak és teljesen felcserélhetők.

ezeknek a szimmetriáknak a megértése megdöbbentő alkalmazásokkal rendelkezik többek között az algebrai geometriában és az algebrai topológiában. Különösen az elmélet korai sikerei közé tartozik az építhető szabályos sokszögek osztályozása, valamint egy tétel, amely azt állítja, hogy a nagyfokú polinomegyenletek nem oldhatók meg gyökökkel.

újabb sikerek jelennek meg a kriptográfiában és Andrew Wiles Fermat utolsó tételének bizonyításában. Ez a bizonyíték magában foglalja a Galois csoport $Gal(\bar{\mathbb Q} /\mathbb Q)$ Csoportos reprezentációval történő tanulmányozását. De azt mondanám, hogy az elmélet valahogy még mindig fiatal, és még sok felfedezésre vár. Végül is ez az egyik legaktívabb kutatási terület a mai tiszta matematikai kutatásban.

ennek arra kell vezetnie minket, hogy sokkal több adót fizessünk Galois hihetetlen zsenialitásáért… hadd tegyek bele egyet a SocraticaStudios-tól.