Az antennák elektromágneses energiát sugároznak az információk továbbítására vagy fogadására. Ezért az energia és az erő kifejezések ezekhez az elektromágneses hullámokhoz kapcsolódnak, és meg kell vitatnunk őket. Az elektromágneses hullámnak mind elektromos, mind mágneses mezője van.

vegye figyelembe a hullámot bármely pillanatban, amely mindkét vektorban megtekinthető. Az alábbi ábra az elektromos és mágneses mező komponenseinek ábrázolását mutatja egy elektromágneses hullámban.

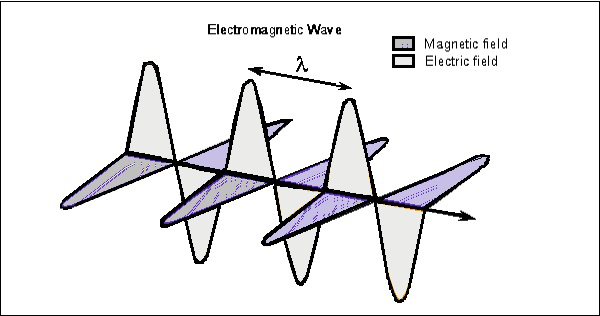
az elektromos hullám függőlegesen van jelen az EM hullám terjedéséhez képest, míg a mágneses hullám vízszintesen helyezkedik el. Mindkét mező derékszögben van egymással.

Poynting Vektor

Poynting vektor leírja az energia az EM hullám egységnyi idő egységnyi területen bármely adott pillanatban az idő. John Henry Poynting először 1884-ben származtatta ezt a vektort, ezért róla nevezték el.

definíció – “a Poynting vektor megadja az egységnyi területre jutó energiaátadás sebességét”

vagy

” azt az energiát, amelyet egy hullám egységnyi időegységenként hordoz, a Poynting vektor adja meg.”

a Poynting vektort a következők jelölik:++.

egységek

a Poynting vektor SI egysége W/m2.

matematikai kifejezés

az elektromágneses hullámokhoz kapcsolódó teljesítmény leírására használt mennyiség a pillanatnyi Poynting vektor, amelyet

$$\hat{S} = \hat{E} \times \hat{H}$$

határozunk meg, ahol

• $\hat{S}$ a pillanatnyi Poynting vektor (W/m2).

• $\hat{E}$ a pillanatnyi elektromos mező intenzitása (V/m).

• $\hat{H}$ a pillanatnyi mágneses mező intenzitása (A/m).

itt fontos megjegyezni, hogy az e nagysága nagyobb, mint H egy EM hullámon belül. Mindkettő azonban ugyanolyan mennyiségű energiát ad hozzá. Az a vektor, amelynek mind iránya, mind nagysága van. Az irányt Ŝ ugyanaz, mint a sebesség a hullám.

A Poynting Vektor levezetése

ahhoz, hogy világos elképzelésünk legyen a Poynting vektorról, menjünk át ennek a Poynting vektornak a levezetésén, lépésről lépésre.

képzeljük el, hogy egy EM hullám, áthalad egy terület (A) merőleges az X-tengely, amely mentén a hullám utazik. Miközben áthalad a-n, végtelen kis időben (dt) a hullám távolságot (dx) tesz meg.

$$dx = C\ dt$$

ahol

$$C = fény sebessége = 3\ alkalommal 10^{8}m/s$$$$kötet, dv = Adx = AC\ dt$$$d\mu = \ mu\dv = (\epsilon_{0}e^{2})(AC\ dt)$$$$= \epsilon_{0} AC\ E^{2} \dt$$

ezért az időben átadott energia (DT) területenként (a) −

$$s = \ frac{energia}{idő\ times terület} = \frac{DW}{dt\a} = \frac {\EPSILON_{0}Ace^{2} \dt}{dt\a} = \ epsilon_{0}C\:E^{2}$$

mivel

$ $ \frac{E}{H} = \ sqrt {\frac {\mu_{0}} {\epsilon_{0}}\ akkor \ S = \ frac{CB^{2}} {\mu_{0}}$$

mivel

$$c = \ frac{E}{H} \ akkor \ S = \ FRAC{EB} {\mu_{0}}$$$$= \hat{S} = \frac{1} {\mu_{0}} (\hat{E} \ hat{H})$$

A Poynting vektort jelöli.

a fenti egyenlet megadja nekünk az időegységre, területegységre jutó energiát az idő bármely pillanatában, amelyet Poynting vektornak nevezünk.