ahol bi (6) az i-edik bin az összes kukák száma (totBins), minD, maxD pedig a minimum, illetve a maximum az SNP-k és az X közötti távolság pozitív valós szám (60), ha x egyenlő 1-gyel, a tartályok közötti távolság eloszlása lineáris, és mindegyik tartálynak azonos a távolságtartománya. Nagyobb x értékek esetén a távolságok eloszlása megváltozik, lehetővé téve, hogy az utolsó tartályokon nagyobb, az első tartályokon pedig kisebb tartomány legyen. Ennek a paraméternek a változtatása lehetővé teszi a felhasználó számára, hogy elegendő számú páros összehasonlítást végezzen ahhoz, hogy hozzájáruljon az egyes kukák végső Ne becsléséhez.

példa alkalmazás

a SNeP-et két közzétett adatkészlettel teszteltük, amelyeket korábban az LD, a Bos indicus és az Ovis aries használatával a ne időbeli tendenciáinak leírására használtak . A szarvasmarha-adatkészletek r2 becsléseit a szerzők a GenABLE (Aulchenko et al., 2007) minimális allélfrekvencia (MAF) használata < 0,01 és a rekombinációs sebesség beállítása Haldane leképezési funkciójával (Haldane, 1919). A juhok adatainak r2 becsléseit a szerzők Plink-1.07 segítségével számították ki (Purcell et al., 2007), MAF < 0,05 értékkel, további javítások nélkül. Mindkét autoszomális adathalmaz esetében R2 becslés, ahol a minta méretére korrigálták a (4) egyenlet alkalmazásával, ahol a (Z) = 2. Ezekhez az összehasonlító elemzésekhez a SNEP parancssor ugyanazokat a paramétereket tartalmazta, amelyeket a közzétett adatokhoz használtak, az r2 becsléseken kívül, a genotípusszám alapján számítva, valamint a SNEP új binning stratégiájának felhasználásával.

eredmények

a SNeP egy többszálú alkalmazás, amelyet C++ nyelven fejlesztettek ki, és a leggyakoribb operációs rendszerek (Windows, OSX és Linux) binárisai letölthetők ahttps://sourceforge.net/projects/snepnetrends/. A binárisokat egy kézikönyv kíséri, amely leírja a SNEP lépésről lépésre történő használatát az Ne tendenciáinak következtetésére az itt leírtak szerint. Az SNeP egy kimeneti fájlt hoz létre tabulátorral tagolt oszlopokkal, amelyek a következőket mutatják az Ne becsléséhez használt minden bin esetében: a múltbeli generációk száma, amelyeknek a bin megfelel (pl., 50 generációval ezelőtt), a megfelelő Ne-becslés, az egyes SNP-párok közötti átlagos távolság a tartályban, az átlagos r2 és az R2 szórása a tartályban, valamint az R2 kiszámításához használt SNP-k száma a tartályban. Ez a fájl könnyen importálható a Microsoft Excel, R vagy más szoftver a telek az eredményeket. Az itt látható ábrák (1., 3. ábra) megfelelnek a kimeneti fájl generációkkal ezelőtti és Ne oszlopainak. Az R2 szórással ellátott oszlop biztosítja a felhasználók számára, hogy megvizsgálják az egyes tartályok ne-becslésének varianciáját, különösen azoknál a tartályoknál, amelyek régebbi időbecsléseket tükröznek, és amelyek kevésbé megbízhatóak, mivel az R2 becsléséhez használt SNP-k száma kisebb lesz.

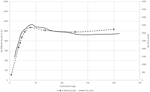
1. ábra. Hat Svájci juhfajta Ne trendjeinek összehasonlítása Burren et al. (2014) (szaggatott vonalak) és ez a munka (folytonos vonalak).

a bemeneti fájlok formátuma a szabványos PLINK formátum (ped és map fájlok) (Purcell et al., 2007). Az SNeP lehetővé teszi a felhasználók számára, hogy vagy kiszámítsák az LD-t a fent leírt adatok alapján, vagy egy egyedi előre kiszámított ld-mátrixot használjanak az Ne becsléséhez az (5) egyenlet segítségével.

a szoftver interfész lehetővé teszi a felhasználó számára az elemzés összes paraméterének, például a BP-ben lévő SNP-k és az elemzéshez használt kromoszómák (pl. 20-23) közötti távolságtartomány vezérlését. Továbbá, SNeP tartalmazza a lehetőséget, hogy válasszon egy MAF küszöb (alapértelmezett 0.05), mivel kimutatták, hogy a MAF elszámolása elfogulatlan r2 becsléseket eredményez, függetlenül a minta méretétől (Sved et al., 2008). Az SNeP többszálú architektúrája lehetővé teszi a nagy adatkészletek gyors kiszámítását (egyetlen kromoszómára ~100k SNP-t teszteltünk), például az itt leírt BOS-adatokat egy processzorral elemeztük 2’43” – ban, két processzor használata 1’43” – ra csökkentette az időt, négy processzor csökkentette az elemzési időt 1’05” – re.

Zebu példa

a zebu elemzéshez a SNEP-vel kapott Ne görbék alakja és a közzétett adattrendek ugyanazt a pályát mutatták, sima csökkenéssel körülbelül 150 generációval ezelőttig, majd egy 40 generációval ezelőtti csúcsú expanzió következett, amely meredek csökkenéssel zárult a legutóbbi generációkhoz képest (1.ábra). Míg azonban mindkét görbe tendenciái azonosak voltak, a két megközelítés eltérő Ne becsléseket eredményezett, az SNeP értékei körülbelül háromszor nagyobbak voltak, mint az eredeti cikkben. Míg elemzéseink során megpróbáltuk a szerzők paramétereit felhasználni, bizonyos különbségek elkerülhetetlenek voltak, azaz az R2-re becsült szarvasmarha-adatok eredeti közzététele a SNeP-ben megvalósított megközelítéstől eltérő megközelítéssel. Az SNEP-vel végzett elemzések genotípusokon alapultak, míg az eredeti elemzés két lókusz haplotípuson alapult, ami azt eredményezi, hogy a közzétett adatok a várható r2 0,32-et mutatnak a minimális távolságon, míg becsléseink 0,23 voltak. Hasonlóképpen, Mbole-Kariuki et al. (2014) R2 = 0,013 háttérszintet kapott 2 Mb körül, míg becslésünk azonos távolságra 0 volt.0035 (az adatok nem jelennek meg). Következésképpen, mivel az LD becsléseink következetesen kisebbek voltak, mint Mbole-Kariuki et al. (2014) várható, hogy Ne becsléseinknek nagyobbnak kell lenniük. Bár ez a megfigyelés kiemeli a paraméterek és küszöbértékek gondos megválasztásának fontosságát, fontos kiemelni, hogy bár az Ne értékek abszolút nagysága eltérő, a tendenciák szinte azonosak.

Svájci Juhpélda

a SNEP-vel elemzett hat Svájci juhfajta összehasonlítható eredményeket hozott az eredeti papíréval (2.ábra), többnyire átfedő Ne trendgörbékkel (3. ábra). Az Ne általános tendenciája azonban hanyatlást mutatott a jelen felé. A SNeP valamivel nagyobb Ne értékeket produkált a távolabbi múltban (700-800 generáció). Ennek oka a SNEP-ben használt eltérő binning rendszer, amely lehetővé teszi a felhasználó számára, hogy egyenletesebb eloszlást érjen el a páros összehasonlítások között az egyes bin-Eken belül (pl., az SNP páros összehasonlítások száma az egyes kukákon belül összehasonlítható). A 400 generációval ezelőtti időtartamon túl Burren et al. (2014) az elemzés során csak három kukát használt (középpontja 400, 667 és 2000 generációval ezelőtt), míg ugyanebben az időszakban a SNeP 5 kukát használt,számos páros összehasonlítással, a 6a, b képletekkel meghatározott tartománytól függően. következésképpen Burren és munkatársai megközelítése a legfrissebb generációkat leíró adatok nagyobb sűrűségével végződik, mint a legrégebbi generációkat. Ezért kevesebb kuka használata növeli a kisebb Ne értékek jelenlétét az egyes kukákban, következésképpen csökkenti az egyes kukák átlagos Ne értékét. A közelmúlt Ne értékei, összehasonlítva a múlt 29. generációjával, nagyon hasonló eredményeket adtak. A legnagyobb különbséget (50) az SBS fajta esetében kaptuk.

2. ábra. A munka 29. generációjában számított legújabb Ne értékek összehasonlítása Burren et al. (2014) hat Svájci juhfajtára.

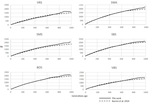
3. ábra. Az elmúlt 250 generáció Ne-trendjeinek összehasonlítása az SHZ-adatokban, amelyeket Mbole-Kariuki et al. (2014) (szaggatott vonal) és a SNEP (folytonos vonal) használata.

megbeszélés

Az Ne elemzését LD adatok felhasználásával először 40 évvel ezelőtt mutatták be, és azóta alkalmazzák, fejlesztették és fejlesztették (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; De Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Az elemzett SNP-k hagyományosan kis száma már nem korlátozás, mivel az SNP chipek rendkívül nagy számú SNP-t tartalmaznak, amelyek rövid idő alatt és elfogadható áron kaphatók. Ez fokozta az emberekre alkalmazott módszer alkalmazását (Tenesa et al., 2007; McEvoy et al., 2011), valamint számos háziasított fajra (Anglia et al., 2006; Uimari és Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Ezekkel a fejlesztésekkel együtt nyilvánvalóvá váltak a módszertani korlátok, amelyekkel itt foglalkoztak, az erőfeszítések többsége a közelmúltbeli Ne helyes becslésére mutatott. A becslés mennyiségi értéke azonban nagymértékben függ a minta méretétől, az LD becslés típusától és a binning folyamattól (Waples and Do, 2008; Corbin et al., 2012), míg kvalitatív mintázata inkább a genetikai információtól függ, mint az adatok manipulációjától.

eddig ezt a módszert különféle szoftverekkel alkalmazták, nincs szabványosított megközelítés az eredmények tárolásához, és minden tanulmány többé-kevésbé önkényes megközelítést alkalmazott, például a generációs osztályok binningjét a múltban (Corbin et al., 2012), binning távosztályokhoz, állandó tartománysal az egyes kukákhoz (Kijas et al., 2012) vagy binning távolságosztályonként lineáris módon, de nagyobb tartályokkal az újabb időpontokhoz (Burren et al., 2014). Tudomásunk szerint az egyetlen rendelkezésre álló szoftver, amely becsüli az Ne-t az LD-n keresztül, a NeEstimator (Do et al., 2014), a korábbi LDNE (Waples and Do, 2008) továbbfejlesztett változata, amely lehetővé teszi a nagy adatkészlet (mint 50K SNPChip) elemzését. Fontos, hogy míg az SNeP a történelmi Ne tendenciák becslésére összpontosít, a NeEstimator célja kortárs elfogulatlan Ne becslések előállítása, ez utóbbit ezért kiegészítő eszköznek kell tekinteni, miközben a demográfiát az LD-n keresztül vizsgálják.

az SNeP-t két olyan adatkészlet elemzésére használtuk, ahol a módszert korábban alkalmazták. A juhokra vonatkozó adatok mind mennyiségi,mind minőségi szempontból összehasonlíthatók voltak a Burren et al. (2014), míg a Zebu-adatokhoz olyan NE trendbecslést kaptunk, amely szorosan megfelelt a Mbole-Kariuki et al. (2014) bár az Ne pontbecslései nagyobbak voltak, mint az adatokhoz leírtak (Mbole-Kariuki et al., 2014). A két eredmény közötti eltérés azt tükrözi, hogy Burren és munkatársai R2 becsléseiket a Plink (a nagyméretű SNP-adatok manipulációjának szabványos szoftvere) segítségével készítették, amely ugyanazt a megközelítést alkalmazza, mint az SNeP R2 becslésére, míg Mbole-Kariuki et al. követte Hao et al. (2007) az r2 becsléshez. Az LD-re vonatkozó különböző becslések használata kritikus fontosságú az Ne görbe mennyiségi aspektusa szempontjából, ahol az Ne és az r2 közötti hiperbolikus korreláció miatt az r2 csökkenése a 0-hoz közelebb eső tartományában nagyon nagy változáshoz vezethet az Ne becslésekben, míg a becslések közötti különbségek kevésbé jelentősek, ha az r2 érték magas, azaz közelebb van az 1-hez. Ezért, bár az egyik adatkészletben az Ne értékek lényegesen eltérőek voltak, mindkét esetben az Ne görbék átfedésben voltak az eredetileg közzétettekkel.

amint azt más szerzők már javasolták, az ezzel a módszerrel kapott kvantitatív becslések megbízhatóságát óvatosan kell figyelembe venni, különösen a legújabb és a legrégebbi generációkhoz kapcsolódó Ne értékek esetében (Corbin et al., 2012), mert az utóbbi generációk számára a c nagy értékei érintettek, nem felelnek meg azoknak az elméleti következményeknek, amelyeket Hayes javasolt a változó becslésére Ne idővel (Hayes et al., 2003). A legrégebbi generációk becslései szintén megbízhatatlanok lehetnek, mivel a Koaleszcens elmélet azt mutatja, hogy a múltban 4Ne generáció után egyetlen SNP-ből sem lehet megbízhatóan mintát venni (Corbin et al., 2012). Továbbá az Ne becsléseit, különösen azokat, amelyek a korábbi generációkhoz kapcsolódnak, erősen befolyásolják az adatmanipulációs tényezők, például a MAF és az alfa értékek megválasztása. Ezenkívül az alkalmazott binning stratégia zavarhatja a módszer általános pontosságát, például ha az egyes kukák feltöltéséhez nem elegendő számú páros összehasonlítást használnak.

a módszer egyik alkalmazása a fajtademográfiák összehasonlítása. Ebben az esetben az Ne görbék alakja lenne az optimális eszköz a különböző demográfiai előzmények megkülönböztetésére, a numerikus értékeiknél jobban, felhasználva őket az adott fajta vagy faj potenciális demográfiai ujjlenyomataként, ugyanakkor figyelembe véve, hogy a mutáció, a migráció és a szelekció befolyásolhatja az Ne becslését az LD-n keresztül (Waples and Do, 2010). Ezenkívül nagyon fontos az SNEP-vel (és más, az Ne becslésére szolgáló szoftverekkel) elemzett adatok gondos mérlegelése, mivel a zavaró tényezők, például a keverék jelenléte az Ne elfogult becsléseit eredményezheti (Orozco-terWengel and Bruford, 2014).

az SNeP célja ezért egy gyors és megbízható eszköz biztosítása az LD módszerek alkalmazásához az Ne becsléséhez nagy áteresztőképességű genotípusos adatok felhasználásával következetesebb módon. Két különböző R2 becslési megközelítést tesz lehetővé, valamint a külső szoftverből származó r2 becslések használatának lehetőségét. A SNeP használata nem lépi túl a módszer és a mögötte álló elmélet határait, mégis lehetővé teszi a felhasználó számára, hogy az elméletet az eddig javasolt összes korrekcióval alkalmazza.

szerzői hozzájárulások

MB fogant és írta a szoftvert és a kéziratot. Az MB, az MT és a POtW tesztelte a szoftvert és elvégezte az elemzéseket. Az MT, a POtW és az MWB felülvizsgálta a kéziratot. Minden szerző jóváhagyta a végleges kéziratot.

összeférhetetlenségi nyilatkozat

a szerzők kijelentik, hogy a kutatást olyan kereskedelmi vagy pénzügyi kapcsolatok hiányában végezték, amelyek potenciális összeférhetetlenségnek tekinthetők.

Köszönetnyilvánítás

köszönjük Christine Flury-nek a juhok adatainak megadását és a hasznos vitát. Köszönetet mondunk a két véleményezőnek a cikk javítására vonatkozó hasznos javaslatokért is. MB támogatta a Program Master and Back (Regione Sardegna).