a fénytörés vagy hajlítás akkor fordul elő, amikor a fény áthalad az egyik közegből a másikba, más törésmutatóval. A fénytörés a lencsék fontos jellemzője, amely lehetővé teszi számukra, hogy egy fénysugarat egyetlen pontra fókuszáljanak, és számos ismert jelenségért is felelős, mint például a vízbe merített tárgyak látszólagos torzulása.

a törésmutató az a relatív sebesség, amellyel a fény áthalad egy anyagon a vákuum sebességéhez viszonyítva. Konvenció szerint a vákuum törésmutatóját úgy definiáljuk, hogy értéke 1,0. Más átlátszó anyagok törésmutatóját, n-t a következő egyenlet határozza meg:

ahol c a fény sebessége, v pedig a fény sebessége az adott anyagban. Mivel a vákuum törésmutatója 1.0 és a vákuum mentes minden anyagtól, ezért az összes átlátszó anyag törésmutatója nagyobb, mint 1,0. A legtöbb gyakorlati célra a levegőn keresztüli fény törésmutatója (1.0003) használható ismeretlen anyagok törésmutatóinak kiszámításához. Néhány gyakori anyag törésmutatóit az alábbi 1. táblázat mutatja be.

anyag fénytörő index levegő 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Például, amikor a fény egy kevésbé sűrű közegből, például levegőből, egy sűrűbb közegbe, például vízbe kerül, az elektromágneses hullám mozgásának sebessége csökken. Alternatív megoldásként, ha a fény sűrűbb közegből kevésbé sűrű közegbe kerül, a hullám sebessége növekszik.

az a szög, amelyen a megtört fény halad, mind a beesési szögtől, mind annak az anyagnak az összetételétől függ, amelybe belép. A normál két anyag közötti határra merőleges vonalként határozható meg. A fény a normálhoz képest szögben jut be a határba, és a Snell-törvény szerint megtörik:

ahol n az 1.és 2. Anyag törésmutatóit jelöli, q pedig az ezen anyagokon áthaladó fény szögeit jelképezi a normálhoz képest. Számos fontos pont vonható le ebből az egyenletből. Ha n (1) nagyobb, mint n(2), a fénytörési szög mindig kisebb, mint a beesési szög. Alternatív megoldásként, ha n (2) nagyobb, mint n(1), a fénytörési szög mindig nagyobb, mint a beesési szög. Ha a két törésmutató egyenlő(n(1) = n (2)), akkor a fény refrakció nélkül halad át.

a törésmutató fogalmát az alábbi 1.ábra szemlélteti, a levegőből az üvegen és a vízen áthaladó fény esetére összpontosítva. Figyeljük meg, hogy míg mindkét gerenda a sűrűbb anyagba ugyanazon beesési szögen keresztül jut be a normálhoz képest (60 fok), az üveg refrakciója majdnem 6 fokkal nagyobb, mint a vízé az üveg nagyobb törésmutatója miatt.

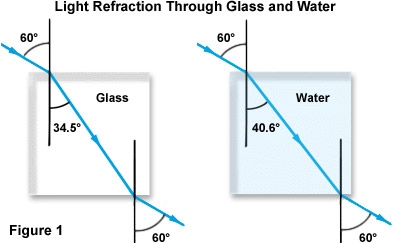
a tudósok azt találták, hogy a törésmutató a fény sugárzási frekvenciájától (vagy hullámhosszától) függ. Ez a jelenség az összes transzparens médiummal együtt fordul elő, és diszperziónak nevezik. Ezért egy átlátszó anyag törésmutatójának mérésekor meg kell határozni a méréshez használt adott hullámhosszt. Az alábbiakban a 2. táblázat részletezi három független hullámhossz diszperzióját különböző közegekben.

anyag kék (486,1 nm) sárga (589,3 nm) piros (656,3 nm) koronaüveg 1,524 1,517 1,515 tűzköves üveg 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Ezt a fényt D vonalspektrumnak nevezik, és a fenti 2.táblázatban felsorolt sárga fényt képviseli. Hasonlóképpen, az F vonal és a C vonal spektruma megfelel a hidrogén által kibocsátott meghatározott hullámhosszú kék és vörös fénynek. Ezek a spektrumok alapvetőek a diszperzió kiszámításában, amely kvantitatív módon meghatározható:

ahol n az anyag törésmutatója egy adott hullámhosszon, amelyet D, F és C jelöl, amelyek az anyag spektrális vonalait képviselik nátrium és hidrogén, amint azt fentebb tárgyaltuk. A kapcsolat olyan, hogy a fény hullámhosszának növekedésével a törésmutató csökken. Azonban számos tényező játszik szerepet a különböző anyagok diszperziójában, beleértve az elemi és molekuláris összetételüket. Számos szervetlen szilárd anyag, például kromátok, dikromátok, cianidok, vanadátok és halogenid komplexek diszperziója szokatlanul magas. A szerves szubsztituensek azonban hozzájárulhatnak a magas diszperzióhoz is.

	Interactive Java Tutorial
fénytörés fedezze fel, hogy a fény hullámhossza és beesési szöge hogyan befolyásolja a fénytörést a különböző törésmutatókkal rendelkező médiumokban.

Refraction of light is particularly important in the construction and physics of lenses. Ne feledje, hogy amikor a fénysugár kilépett mind az üvegből, mind a vízből az 1.ábrán, ismét ugyanabban a szögben tört meg, amelyben belépett az anyagba. Ez a koncepció elengedhetetlen a lencsék működésében, bár a lencse alakja jelentősen befolyásolja a kapott képet. Egy domború lencsében, amint azt az alábbi 2. ábra szemlélteti, a tárgyról, jelen esetben egy zsiráfról visszaverődő fényhullámok a lencse optikai középpontja felé hajlanak, és a fókuszponton konvergálnak.

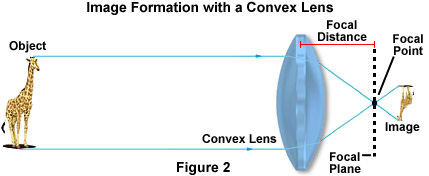
Az objektumnak az objektív elülső fókuszpontjához viszonyított relatív helyzete határozza meg az objektum leképezését. Ha az objektum túl van a fókuszpont kétszeresén, akkor kisebbnek és fordítottnak tűnik, és egy további lencsével kell leképezni a méret nagyításához. Ha azonban a kép közelebb van a lencséhez, mint a fókuszpont, a kép függőlegesen és nagyobbnak tűnik, amint azt egy egyszerű nagyítóval könnyen meg lehet mutatni.

	Interactive Java Tutorial
Kép nagyítás fedezze fel, hogyan nagyítja a zsiráf képét az egyszerű vékony, két domború lencsén áthaladó fényhullámok fénytörése.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Egy egyszerű ivószalma egy vízzel töltött pohárban, amint azt a 3. ábra szemlélteti, kiváló példa erre az előfordulásra. Ebben a példában a fényhullámoknak először át kell haladniuk a vízen, majd az üveg/víz határon, végül a levegőn. A szalma végeiről visszaverődő fényhullámok nagyobb mértékben törnek meg, mint a szalma közepéből érkező fényhullámok, így a szalma nagyítottnak és kissé eltorzultnak tűnik.

ugyanez a jelenség használható egy folyadék törésmutatójának optikai mikroszkóppal történő meghatározására. Ehhez egy lapos cellát kell elhelyezni, amely képes jelöléssel (vagy beosztásokkal) ellátott folyadékot tartani az üveg belső felületén. Szintén, az egyik mikroszkóp okulárnak az elsődleges képsíkba beosztott retikulummal kell rendelkeznie a jel vonalszélességének méréséhez a lapos cellában. Mielőtt az ismeretlen törésmutatójú folyadékot hozzáadnánk a sejthez, a mikroszkópot a sejt alján lévő jelre kell összpontosítani, és meg kell mérni a jel helyzetét a retikulumon. Ezután kis mennyiségű folyadékot kell hozzáadni a sejthez, és a mikroszkópot újra kell fókuszálni a jelre (a folyadékon keresztül), és új mérést kell végezni. Ezután a mikroszkópot végül a folyadék felületére kell összpontosítani, majd egy harmadik leolvasást rögzíteni kell a jel helyzetének mérésével a retikulumon. Az ismeretlen folyadék törésmutatója ezután a következő egyenlet segítségével számítható ki:

ahol D(mért) a mikroszkóp segítségével mért mélység (a folyadék felszínétől az üres cellán lévő jel helyzetéig), D(látszólagos) pedig a mikroszkóp segítségével mért jelmérés folyadék nélkül.

a fényvisszaverődés kritikus szöge egy másik kulcsfontosságú fogalom a fénytörés vizsgálatában, amelyet az alábbiakban a 4.ábra mutat be. Amikor a fény magas törésmutatójú közegen halad át alacsonyabb törésmutatójú közegbe, a fényhullámok beesési szöge fontos tényezővé válik. Ha a beeső szög egy meghatározott értéken túl növekszik (a két közeg törésmutatójától függően), akkor elér egy olyan pontot, ahol a szög olyan nagy, hogy egyetlen fény sem törik meg az alacsonyabb törésmutató közegébe.

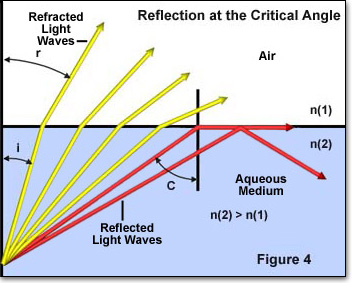
A 4.ábrán az egyes fénysugarakat piros vagy sárga színű nyilak képviselik, amelyek a magas törésmutatójú közegből (n(2)) az alacsonyabb törésmutatójú közegbe (n(1)) mozognak. Az egyes fénysugarak beesési szögét I jelöli, a fénytörési szöget pedig r.a négy sárga fénysugár mindegyikének beesési szöge (i) elég alacsony ahhoz, hogy áthaladjon a két közeg közötti interfészen. A két vörös fénysugár beeső szöge azonban meghaladja a kritikus szöget (körülbelül 41 fok), és vagy a közeg közötti határba, vagy a magas törésmutatójú közegbe visszaverődik. Ez a jelenség akkor következik be, amikor a fénytörési szög (r szög a 4. ábrán) 90 fokkal egyenlő lesz, és Snell törvénye a következőre redukálódik:

ahol (q) – t most kritikus szögnek nevezzük C. Ha a kisebb törésmutatójú Közeg Levegő (n = 1.00), Az egyenlet tovább csökken:

amint azt korábban tárgyaltuk, a fénytörés másik fontos jellemzője, hogy a fény hullámhossza hatással van a közegben bekövetkező fénytörés mennyiségére. Valójában a fénytörés mennyisége fordítottan arányos a beeső fény hullámhosszával. Így a rövidebb hullámhosszú látható fény nagyobb szögben megtörik, mint a hosszabb hullámhosszú fény. Következésképpen, amikor a fehér fényt, amely a látható spektrum összes színéből áll, egy üvegprizmán vezetik át, akkor az egyes hullámhosszaktól függő módon oszlik el az alkotó színeiben. Az alacsony frekvenciájú látható fény (600 nanométer vagy annál nagyobb) kisebb szögben törik meg, mint a nagyobb frekvenciájú fény, ami szivárványszerű hatást eredményez, amint azt az 5.ábra szemlélteti.

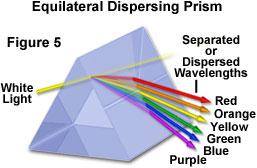
ugyanez a jelenség felelős a kromatikus aberrációért is. Amikor a fehér fényt egy egyszerű konvex lencsén vezetik át, több fókuszpont keletkezik a közvetlen közelében, amelyek megfelelnek a komponens hullámhosszainak kisebb törésmutató-különbségeinek. Ez a hatás általában színes (piros vagy kék, a fókusztól függően) halókat eredményez, amelyek körülveszik az objektumok képeit. Ennek az aberrációnak a korrekcióját általában két vagy több lencsetag kombinációjával hajtják végre, amelyek különböző diszperziós tulajdonságokkal rendelkező anyagokból állnak, például egy akromatikus lencse, amely mind koronával, mind kovakőüveggel készült.

	Interactive Java Tutorial
fénytörés prizmával vizsgálja meg, hogy a prizma különböző szögein keresztüli fénytörés hogyan választja el a fehér fényt alkotó színeire.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. A leggyakoribb példa egy kamera, amelyet arra terveztek, hogy éles és fókuszált képeket hozzon létre egy film emulziójára vagy egy töltéscsatolt eszköz (CCD) felületére, hogy pontos képet készítsen. A fény ezen jellemzőit kihasználó egyéb optikai eszközök közé tartoznak a mikroszkópok és a távcsövek, amelyek lehetővé teszik az emberi szem számára láthatatlan tárgyak megtekintését, függetlenül attól, hogy egy tű fején vagy egy távoli galaxisban helyezkednek-e el.

közreműködő szerzők

Mortimer Abramowitz-Olympus America, Inc., Két Vállalati Központ Meghajtó., Melville, New York, 11747.Shannon H. Neaves és Michael W. Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida Állami Egyetem, Tallahassee, Florida, 32310.

vissza a fényhez és a színhez

kérdése vagy észrevétele van? Küldjön nekünk egy e-mailt.

1998-2021 között Michael W. Davidson és a Floridai Állami Egyetem. Minden jog fenntartva. A szerzői jogok tulajdonosainak engedélye nélkül semmilyen kép, grafika, szkript vagy kisalkalmazás nem reprodukálható vagy használható fel. A weboldal használata azt jelenti, hogy elfogadja a tulajdonosok által meghatározott összes jogi feltételt.

ezt a weboldalt a mi
Graphics &Web programozó csapat
együttműködve optikai mikroszkópia a
nemzeti nagy mágneses mező laboratórium.

Utolsó módosítás: péntek, November 13, 2015 A 02:18 PM

hozzáférés száma március óta 10, 2003: 181405

látogasson el a weboldalak partnereink az oktatásban: