a Gauss egy folyamatos függvény, amely alatt a terület 1. Ez lehetővé teszi számunkra a valószínűségek ábrázolását. A normális eloszlás valószínűségén vagyunk. A Kálmán-szűrők uni-modalitása azt jelenti, hogy minden alkalommal egyetlen csúcsunk van a rendszer állapotának becsléséhez.

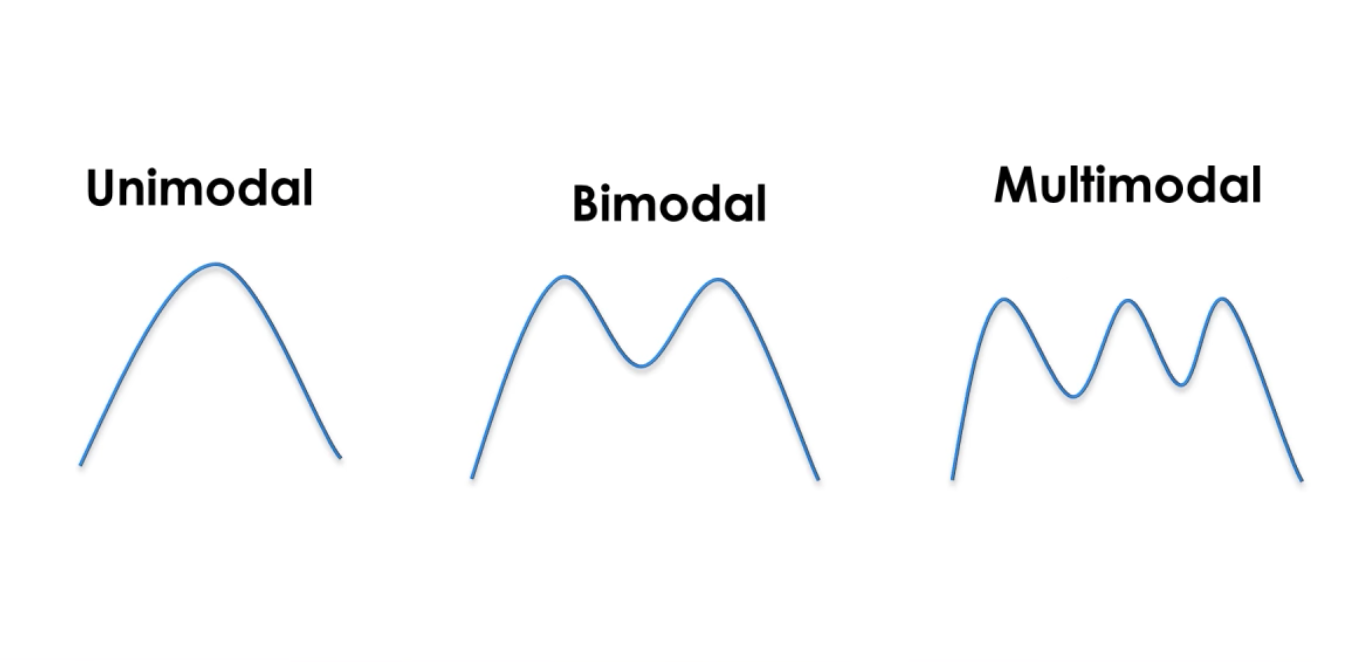
van egy állapotokat képviselő átlagunk, és egy bizonytalanságot képviselő varianciánk, a 2. Minél nagyobb a variancia, annál nagyobb a bizonytalanság.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Érzékelőink megfigyeléseit arra használjuk, hogy korrigáljuk az előrejelzett állapotot, és pontosabb becslést kapjunk.

a becsléshez a Kálmán-szűrőnek csak az aktuális megfigyelésekre és az előző előrejelzésre van szüksége. A mérési előzmények nem szükségesek.

matematika

a Kálmán szűrők mögött álló matematika mátrixok összeadásából és szorzásából áll. Két szakaszunk van: előrejelzés és frissítés.

predikció
előrejelzésünk abból áll, hogy megbecsülünk egy X’ állapotot és egy P’ bizonytalanságot t időben az előző X és P állapotokból t-1 időpontban.

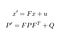
• F: átmeneti mátrix a T-1-től t-ig
• 6: hozzáadott zaj
• Q: Kovariancia mátrix, beleértve a zajt

frissítés
a frissítési fázis egy érzékelő z méréséből áll, hogy korrigáljuk az előrejelzésünket, és így megjósoljuk az x-et és a P-t.

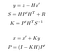
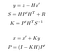
képletek frissítése

• y: különbség a tényleges mérés és az előrejelzés között, azaz a hiba.
• S: becsült rendszerhiba
• H: az érzékelő markere és a miénk közötti átmenet mátrixa.
• R: Az érzékelő zajához kapcsolódó kovariancia mátrix (az érzékelő gyártója adja meg).
• K: Kálmán gain. A 0 és 1 közötti együttható tükrözi az előrejelzésünk korrekciójának szükségességét.

a frissítési fázis lehetővé teszi egy x és egy P becslését közelebb a valósághoz, mint amit a mérések nyújtanak.

a Kálmán-szűrő valós időben, előzetes adatok nélkül teszi lehetővé a jóslatokat. A mátrixok szorzásán alapuló matematikai modellt használunk minden alkalommal, amikor meghatározzuk az X állapotot (pozíció, sebesség) és a P bizonytalanságot.

representation prior/Posterior

Ez az ábra azt mutatja, hogy mi történik a Kálmán-szűrőben.

• az előrejelzett állapotbecslés az első becslésünket, az előrejelzési fázisunkat jelenti. A prior-ról beszélünk.
• a mérés az egyik érzékelőnk által végzett mérés. Jobb a bizonytalanság, de az érzékelők zaja olyan mérést tesz lehetővé, amelyet mindig nehéz megbecsülni. A valószínűségről beszélünk.
• az optimális Állapotbecslés a frissítési fázisunk. A bizonytalanság ezúttal a leggyengébb, információkat halmoztunk fel, és lehetővé tettük, hogy biztosabb értéket hozzunk létre, mint csak az érzékelőnkkel. Ez az érték a legjobb tippünk. Posterior-ról beszélünk.

amit a Kalman szűrő valósít meg, az valójában Bayes-szabály.

egy Kálmán-szűrőben a mérésekből származó előrejelzéseket hurkoljuk. Előrejelzéseink mindig pontosabbak, mivel bizonyos mértékű bizonytalanságot tartunk fenn, és rendszeresen kiszámoljuk a jóslatunk és a valóság közötti hibát. Mátrixszorzásokból és valószínűségi képletekből képesek vagyunk megbecsülni a körülöttünk lévő járművek sebességét és helyzetét.

“Extended/Unscented” szűrők és nemlinearitás

alapvető probléma merül fel. Matematikai képleteink mind y = ax + b típusú lineáris függvényekkel vannak megvalósítva.
a Kalman szűrő mindig lineáris függvényekkel működik. Másrészt, ha radart használunk, az adatok nem lineárisak.

a radar három méréssel látja a világot:

Ez a három érték teszi mérésünket nemlineárisvá, figyelembe véve a szöget is.

itt az a célunk, hogy az adatokat konvertáljuk a (Z) adatokból (px, py, vx, vy).

Ha nemlineáris adatokat adunk meg egy Kálmán-szűrőben, akkor az eredményünk már nem uni-modális Gauss formában van, és már nem tudjuk megbecsülni a pozíciót és a sebességet.

auss vs non-linearitás

tehát közelítéseket használunk, ezért két módszeren dolgozunk:
– a kiterjesztett Kalman szűrők jacobian és Taylor sorozatokat használnak a modell linearizálásához.
– illat nélküli Kalman szűrők pontosabb közelítést használnak a modell linearizálásához.

a nem linearitás Radar általi beépítésének kezelésére léteznek technikák, amelyek lehetővé teszik szűrőink számára a követni kívánt objektumok helyzetének és sebességének becslését.