アンテナは、情報を送信または受信するために電磁エネルギーを放射します。 したがって、エネルギーとパワーという用語はこれらの電磁波に関連しており、それらを議論する必要があります。 電磁波は電場と磁場の両方を持っています。

両方のベクトルで見ることができる任意の瞬間の波を考えてみましょう。 次の図は、電磁波における電界成分と磁界成分の表現を示しています。

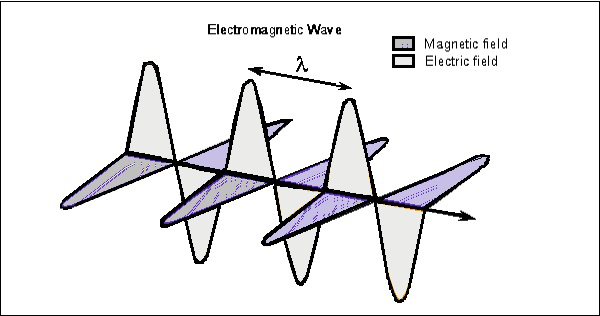
電磁波はEM波の伝播に垂直に存在し、磁気波は水平に位置しています。 両方のフィールドは互いに直角になっています。

ポインティングベクトル

ポインティングベクトルは、任意の時点での単位面積あたりの単位時間あたりのEM波のエネルギーを記述します。 ジョン-ヘンリー-ポインティングは1884年にこのベクトルを最初に導出したため、彼にちなんで命名された。

定義−「ポインティングベクトルは、単位面積あたりのエネルギー移動の速度を与える」

または

「波が単位面積あたりの単位時間”

ポインティングベクトルはΠで表されます。

単位

ポインティングベクトルのSI単位はW/m2です。

数式

電磁波に関連付けられている電力を記述するために使用される量は、次のように定義されている瞬時ポインティングベクトルです。

hat\hat{s}=\hat{e}\times\hat{h}ここで、

• hat\hat{s}.は瞬時ポインティングベクトル（w/M2）である。hat\hat{E}.は瞬時電界強度（V/m）です。hat\hat{H}.は瞬時磁場強度（A/m）です。ここで注意すべき重要な点は、Eの大きさがEM波の中でHよりも大きいことです。 しかし、それらの両方が同じ量のエネルギーを寄与する。 Θはベクトルで、方向と大きさの両方を持ちます。 Θの方向は波の速度と同じです。 その大きさはEとHに依存します。

  ポインティングベクトルの導出

  ポインティングベクトルについて明確なアイデアを得るために、このポインティングベクトルの導出を段階的なプロセスで行ってみましょう。

  EM波が波が移動するX軸に垂直な領域（A）を通過すると想像してみましょう。

  EM波が移動する領域（A）を通過すると想像してみましょう。

  Aを通過している間、無限小時間（dt）で、波は距離（dx）を移動します。

  $$dx=C\dt$$

  ここで、

  $$C=速度\り軽=3\times10^{8}m/sお$$$$量、dv=Adx=AC\dt$$$$d\mu=\mu\dv=(\epsilon_{0}E^{2})(AC\dt)$$$$=\epsilon_{0} AC\E^{2}\dt$$

  このため、エネルギー転時間(dt)単位面積当たりの(A)−

  $$S=\frac{エネルギーを}{時間\times地域}=\frac{dW}{dt\A}=\frac{\epsilon_{0}ACE^{2}\dt}{dt\A}=\epsilon_{0}C\:E frac{e}{H}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}\then\s=\frac{cb^{2}}{\mu_{0}}since

  以来

  c c=\frac{e}{h}\Then\S=\frac{eb}{\MU_{0}}\Then\S=\frac{eb}{\MU_{0}}\then\S=\frac{eb}{\MU_{0}}\then\S=\frac{eb}{\MU_{0}}\then\S=\frac{eb}{\MU_{0}}\then\S=\frac{eb}{\MU_{0}}\then\S=\frac{eb}{\MU_{{0}}$$$$= \hat{S}=\frac{1}{\mu_{0}}（\hat{E}\hat{H}）pはポインティングベクトルを表します。上記の式は、ポインティングベクトルと呼ばれる任意の時点での単位時間当たりの単位面積当たりのエネルギーを与えます。

  上記の式は、ポインティングベクトルと呼ばれる単位時間当たりのエネルギーを与えます。

  広告
  広告

  広告