確率分布>三角分布

三角分布とは何ですか？三角形分布（三角形分布と呼ばれることもあります）は、三角形のような形をした連続確率分布です。

三角形分布（三角形分布と呼ばれることもあります）は、 それはによって定義されます：

• a：最小値、ここでa≤c、
• c：ピーク値（三角形の高さ）、ここでa≤c≤b、
• b：最大値、ここでb≤c。

これにより、サンプルデータから分布のパラメータを推定することが非常に簡単になります。

• aの推定量としてサンプル最小値を使用し、
• bの推定量としてサンプル最大値を使用し、
• cの推定量として任意の合理的な統計量（サンプル平均、モード、中央値など）を使用します。

サンプルデータがない場合は、専門知識を使用して推定可能な最小値を推定することができます。

サンプルデータを持っていない場合は、専門知識を使用して推定可能な最小値を推定することができます。

、最大値と最も可能性の高い値（すなわち、モード）。

三つのパラメータ、bとcは、三角形の形状を変更します: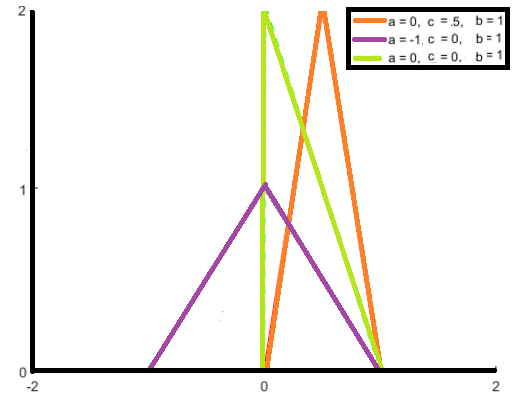

すべての確率分布と同様に、曲線の下の面積は1です。 したがって、aとcの間の距離（すなわち範囲）が広いほど、高さは短くなります。 ピークがゼロを中心とし、a=bのとき、それは対称三角分布と呼ばれます。

ピークがゼロを中心とし、a=bのとき、それは対称三角分布と呼ばれます。 これが起こると、aとbは等しいが符号が反対（例えば-2,2）であり、aとbの代わりに-aとaと呼ばれることがあります。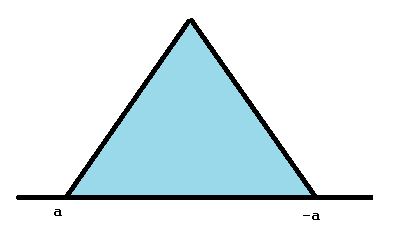

PDF、平均および標準偏差

確率密度関数は、確率変数が特定の範囲に入る確率を見つけるために使用され、次のように与えられます。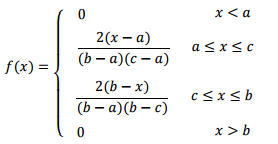

この分布の平均は次のとおりです。
μ=1/3()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()a+b+c）。

標準偏差sは、次のとおりです。
s=(1/√6)a.
この式は、分布がゼロを中心とし、エンドポイントが既知であると仮定します。

リファレンス：
サミュエル-コッツ、Sとヴァン-ドープ。J.(2004)Beyond Beta. 三角分布に関するサンプル章は、World Scientificから入手できます。

——————————————————————————

宿題やテストの質問の助けが必要ですか？ Cheggの調査を使うと、分野の専門家からのあなたの質問に段階的な解決を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です！