渦度
流体力学の不可欠な部分は渦度です。 ヒューリスティックには、流体パーセルの局所回転を測定します。 固体物体の場合、物体の渦度については言及しませんが、代わりにその角速度を参照します。 これらの2つの概念は関連していますが、流体のように変形する回転物体を議論するときには、渦度がより便利です。
与えられた平面内の与えられた速度場の渦度は、その平面内の任意の二つの直交軸を選択し、各軸の角速度を加算することによって計算されます。
固体の物体、または固体の物体のように回転する流体(適切には固体の回転と呼ばれる)では、各軸が同じ速度で回転するため、渦度は角速度の2倍です。 しかし、流体では、2つの軸は非常に異なる速度、さらには異なる方向で回転することができます! 各軸は回転することができますが、正味の渦度はゼロである可能性もあります(非回転渦を参照)。流体の運動が厳密に平面内にあるように制限されている場合、渦度ベクトルは平面に直交するとみなされ、方向(または傾き)を変更することはできま 変化する可能性のある渦度の唯一の側面は、その大きさです。 このエネルギーのより大きなスケールへの移動は、木星上の大きな赤い斑点の形成と関連していると考えられている。
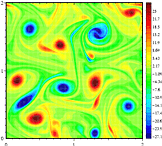
三次元流体運動では、渦度ベクトルは、各軸、x、y、zに平行な成分を持つという点で三次元です。z成分はz軸に平行であり、xy平面 この二分法のために、二次元乱流と三次元乱流との間に挙動に定性的な違いがある。 前者では渦が凝集して大きな渦を形成する傾向があり,後者では渦運動が引き裂かれ,エネルギーは最小スケールまでカスケードして拡散する。

数学的には、与えられた速度場の渦度、
![]()
は速度場のカールであると定義され、通常はギリシャ文字omegaで表されます。
![]()
iv id=”オメガ”
iv id=”オメガ”
iv id=”オメガ”
iv id=”オメガ”
iv id=”オメガ”
iv id=”オメガ”
iv id=”オメガ”
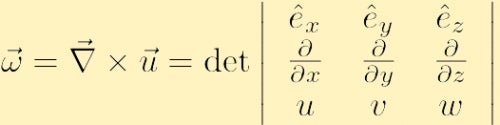 eq2
eq2
ここで、勾配に従来のnablaシンボルを使用しました:
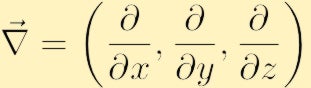
成分形式では、渦度は上記の行列式を展開することによって見出され、
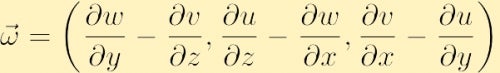
渦度に関連する流体力学のもう一つの重要な側面は循環である。 空間内のすべての点で定義される局所的性質である渦度とは異なり、循環は曲線上の流体の性質を積分することによって定義される大域的性質で 特に、閉じた輪郭を選んで文字C(t)で表すと、反時計回りのC(t)の周りの循環は、で表されるスカラー量です。
![]()
は、
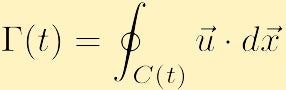
これは、次のように定義されています。閉じた輪郭ができるように、時間。これが物理的に何を言っているのかを説明するために少し時間を取ってみましょう。
ContourC(t)上のすべての点で、曲線に接する速度の成分を見つけ、このスカラーに無限小の長さを掛けます; 接線上に速度を投影すると、必然的にその位置での速度とゼロの間の大きさが得られます。 速度が曲線に接している場合、速度が曲線に直交している場合、速度はゼロになります。 次に、この量を輪郭の周りに無限の数のものを合計するという別の方法で統合して、すべての点からの寄与を追加します。 このことから、輪郭C(t)に沿った循環は、輪郭c(t)の周りの流れの量であることがわかります。; 正または負の結果は、それぞれ時計回りまたは時計回りの循環を等高線に対応します。 極端な場合の1つは、速度場が曲線C(t)に対して垂直などこにでもあり、流れが常に輪郭を横切って輪郭に沿って流れることがないため、循環がない ゼロ以外の循環を得るには、流れが閉じた輪郭に沿っている曲線の一部がなければなりません。
速度場が滑らかで、C(t)内に特異点がない場合、ベクトル計算からストークスの積分定理を使用して循環を次のように書き換えることができます。
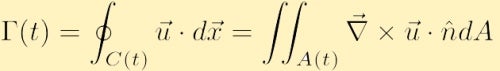
ここで、Aは輪郭C内に含まれる面積であり、θは面積に対する単位法線ベクトルである。
循環のためのこの新しい方程式を考える前に、ベクトル場が速度であるストークスの定理の物理的な意味を理解することは有用です。
ベクトル場が速度であることを理解することは有用です。
ベクトル場が速度であること 上記の二重積分では、輪郭内のすべての点で渦度を計算し、A(t)内のこれらの点すべての渦度を合計します。 閉じた輪郭上の単一積分では、領域の境界に沿った流れを計算しています。 ストークスの定理によれば、これらの量は等しいので、ある領域内に平均渦度があり、その領域がゼロ以外の回転速度を持つことを意味しなければならない場合、その境界の周囲に沿って正味の循環が存在しなければならないと述べている。
微積分の平均値定理から、二重積分の被積分関数をC(t)がある平面に直交する渦度の平均成分に対応する平均値に置き換えることができます。 したがって、循環の第二の解釈は、それが平均渦度×C(t)内に含まれる面積であるということである。 閉じた輪郭C(t)上の循環を計算する代わりに、A(t)に垂直な平均渦度を計算し、それに内の面積を掛けることができます。 渦度がどこでも一定である特別なケースを考慮すると、循環は渦度の大きさに含まれる面積を掛けたものになります。
点渦は面積を持たない渦であり、渦度は単一の点にのみ存在することを意味する。 点渦を研究するために、我々は最初に我々が2D非圧縮性流れを持っていると仮定する。 (点渦は、3Dで見たときに線渦と呼ばれることもあります。)
いくつかの計算の後、z0に位置する複雑な形の点渦によって生成される速度場は、(ガンマゼロは点渦の周りの循環であり、点渦の強さと呼ばれることが多い)で与えられることを決定する。
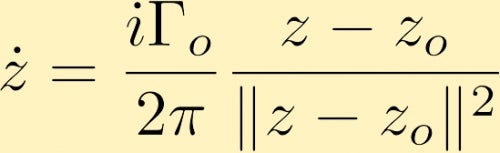
ある点渦によって生成される速度場は、別の点渦を移動させる可能性がある。 ここでは、このいくつかの例があります: 二つの点渦は、正と等しい大きさの両方、二つの点渦は、両方の正が、一方は他方の三倍の強さを有し、一方の点渦は正である他の二倍の大きさで負である。 別の可能性は、同じ大きさではあるが符号が反対の2つの点渦を考慮することである。
これは任意の数の点渦Nに拡張することができます。:点渦の相互作用を見ることは非常に興味深い問題であり、特に点渦の数が増加するにつれて解析的に行うことは困難である。 このように点渦相互作用の数値シミュレーションは非常に一般的である。 大きな点渦シミュレーションの有用なアプリケーションの一つは、有限の面積を持つ渦をシミュレートする点渦の大きなクラスタを見る場合です。 ここでは,いくつかの大きな点渦シミュレーションの説明と結果を示した。 この場合,等しい強さの点渦の二つの大きなクラスタが合併している。 次のケースでは、クラスタ化された点のveracitiesのリングから始めます。
渦度の進化の方程式を見つけるために、運動量方程式から始めます。 運動量方程式では、移流項は次のように書き換えることができます。
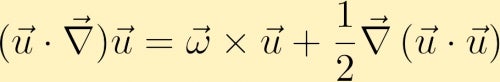
次に運動量方程式のカールを計算し、いくつかのベクト:渦度方程式は、流体中で渦度がどのように生成されるかを示しています。 一般性を失うことなく、最初はz方向に渦度しかないと仮定します。 このことから、4つの異なる項のそれぞれが渦度をどのように変化させることができるかを見ることができます。
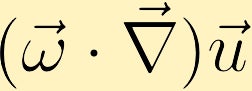
既存の渦度の方向に速度の変化がある場合、渦度を生成することができます。
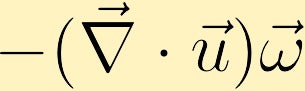
流体パーセルが拡大しており、渦度が正の場合、流体パーセルの渦度は減少し、パーセルが収縮している場合、渦度は増加します。p>

一定の密度(アイソピクナル)の流体層は、一定の圧力(アイソバー)の層と一致したいと考えています。 これらの層が一致しない場合、流体はそれらを整列させるために回転し始め、渦度が生成される。 (この例では、ゼロ渦度から始めます。)
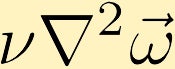
粘性力は渦度の拡散を引き起こします。 (この例では、中心に無限の渦度の点から始めます。)