革命的なガロア理論

月31、1832年、Évariste Galoisと呼ばれるフランスの共和党革命家が銃声で死亡した。 20歳だった。 前の晩、彼自身の死を恐れて、ガロアは熱狂的に”私は時間がない、私は時間がない”と落書き、多くの手紙を書いていました。 一つの文字は、歴史的な理由のために特に貴重です。 この手紙の中で、ガロアは実際に革命を引き起こしたと主張しています。 政治的なものではありません。 しかし、数学的なもの。
ガロワが始めた革命は、彼が想像していたよりも大き その子孫が上昇し、数学の世界を引き継いでいるように数学の風景は、ガロアのビジョンによって深く影響されています。 この子孫は現在遍在しており、無制限の土地を支配しています。 それは純粋な代数の名前の下に行きます。ガロアの劇的な人生の物語をもう少しロマンチックにするために、ここで私が代数について作ったドキュメンタリーの要約です:

彼は間違いなくです! しかし、彼の数学的革命はスムーズに行かなかった。 すべての革命指導者のように、彼は最初に最大限の困難を抱えていました。 革命を想像しないように。 しかし、数学へのゲームを変えるアプローチで彼に参加するために他の人を説得する。 ガロアがまだ生きていたとき、彼の革命的なアイデアはフランスの科学アカデミーによって数回拒否されました…Siméon Denis Poissonのような当時の最高のフランスの数学者はそれを得ることができなかったからです! 部分的にガロアの読めない手書きのために右に表示されました…
div 私はこれが本当にガロアの革命を引き起こしたと思います!
それは間違いなく大きな後押しでした。 しかし、偉大なオーストリアの数学者エミールアルティンは最終的にガロア理論にその現代的な形を与えるために、1942年に別の82年かかるだろう。 アルティンは多くのクレジットに値する。 ガロアはこの革命を予見した先見の明であったが、アルティンは、多くの意味で、実際に革命を引き受け、数学を覆した人です。 アルティン、およびいくつかの他のおかげで、今日、ガロア理論は(フェルマーの最後の定理のワイルズの証明のような)驚くべきと驚くべき成果をたっぷりと、数学の研究の避けられない礎石となっているだけでなく、オープンな質問や謎の巨大な貯水池!この記事は、ますます知的にあなたをプッシュしようとしています。
純粋代数の体
ガロア理論は数の対称性についてです。 しかし、そこに着く前に、私はあなたが数字についての秘密をさせることによって武装させるために紹介する必要があります。 そして、私はあなたがそれを聞いたと確信しています! 確かに、高校に戻って、あなたはおそらく分母に根を残すことは決して教えられませんでした。どういう意味ですか?
これは私に鐘を鳴らします…しかし、私たちが何をすべきか覚えていません…
へへ…私たちは分母の共役で上下に乗算するように教えられました。 この共役は得られた置き換え$-$よ$+$(またはその逆)の分母
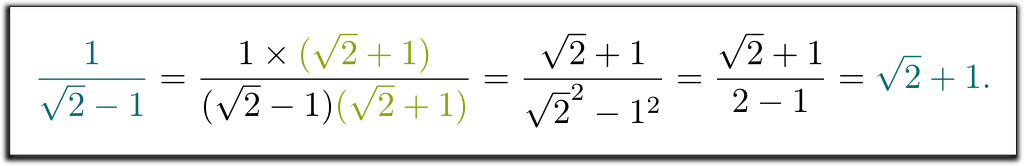
わかっている! 複雑な式/1/(\sqrt{2}-1).はsqrt\sqrt{2}+1.と同じ数を表します。 そして、これは私たちの教師が私たちが他の方法ではなく一つの方法で結果を書くことを望んでいた理由を説明しています:すべてが同じ方法で書
div 私は彼らのポイントを参照してください!しかし、what1/(\sqrt{2}-1)aboutはどうですか? 分母の根を取り除くことはできますか? それも行うことができますか?
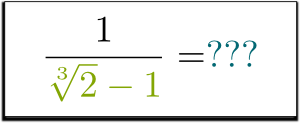
わかっている!では、どのようにして分母から立方体の根を取り除くことができますか?あなたは私に教えてください!
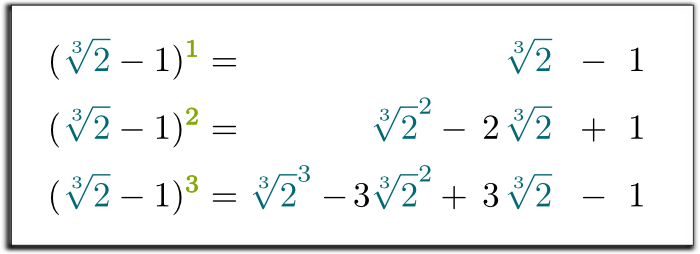
それはそうです! これにより置換の方程式になることを示し、第三国の$\sqrt{2}-1$書き込については、合理的な数の$\sqrt{2}$と$\sqrt{2}^2$!
最初の2行に3を掛けて、3つの方程式をすべて加算しましょう。
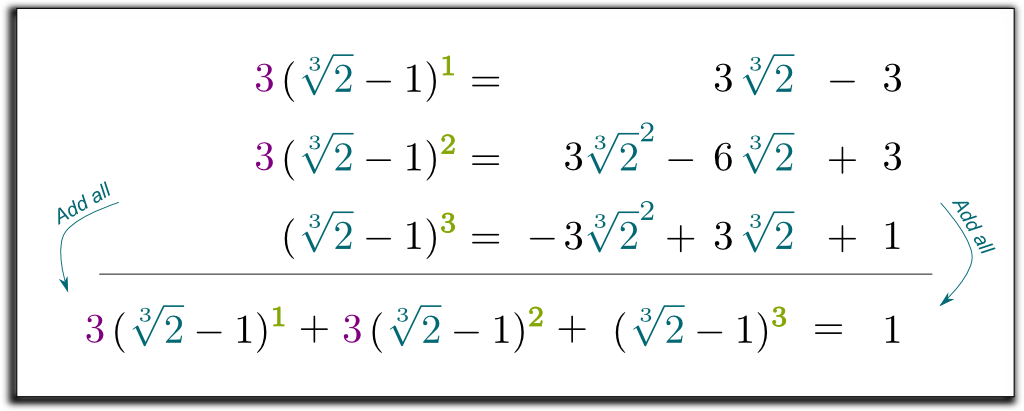
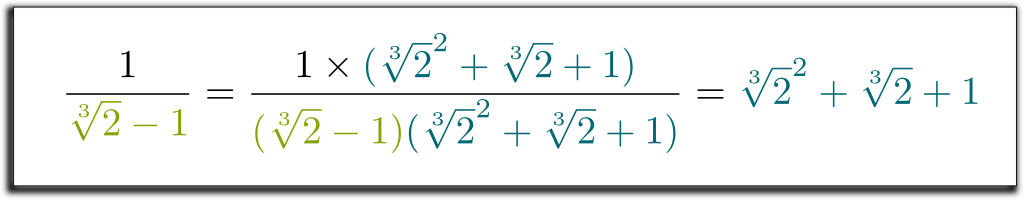
わかっている! しかし、私たちが使用した方法は非常に一般的であるということさえきちんとしています! 同様の技術で、分母からすべてのラジカルを削除できるようになりました!
mathbb mathbb Q{2}]/\mathbb Q$がフィールド拡張であるという事実は、2つのフィールド間の非常に自然な接続をもたらします。 つまり、mathbb\mathbb Q{2}]vectorはベクトル空間と見なすことができます。.\mathbb Q$はスカラーフィールドです。 特に、その人々の所得や社会的地位は各人の$\mathbb Q{2}]$書き込みでき$a\sqrt{2}^2+b\sqrt{2}+c$と$(1,\sqrt{2},\sqrt{2}^2)$的の$\mathbb Q{2}]$と$\mathbb Q$-ベクトル空間です。 そして、これは幾何学的に3次元空間として表現できることを意味します!P>
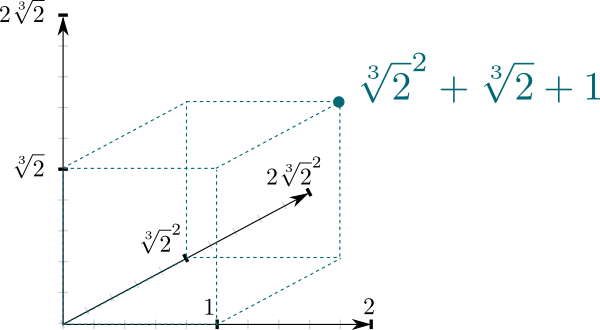
上のベクトル空間の次元は体の拡張の興味深い性質である。
これは次数として知られており、一般的にはbig big{2}]:\mathbb Q\big]=3.と表されます。
はい! これのフィールド拡張を作成するのは実際には非常に簡単です:mathbb\mathbb Q{2}]]に属していないいくつかの根本的な数を追加するだけです!同様に、私はsqrt\sqrt{2}addを追加することができますか?
はい! これにより、フィールド$(\mathbb Q{2}])=\mathbb Q{2}、\sqrt{2}].が作成されます。 このフィールドには、products\sqrt{2}.とsums\sqrt{2}.の積と合計であるすべての数値が含まれています。 これらの形式は、次のとおりです$a\sqrt{2}^2$+$b\sqrt{2}+c$+$d\sqrt{2}^2\sqrt{2}$+$e\sqrt{2}\sqrt{2}$+$f\sqrt{2}$. 次数degree big{2}、\sqrt{2}]:\mathbb Q{2}]\big]$が何であるかについてのアイデアはありますか?
はい! そして、$a\sqrt{2}^2$+$b\sqrt{2}$+$c$+$d\sqrt{2}^2\sqrt{2}$+$e\sqrt{2}\sqrt{2}$+$f\sqrt{2}$=$(a\sqrt{2}^2+b\sqrt{2}+c)$+$(d\sqrt{2}^2+e\sqrt{2}+f)\sqrt{2}$. このように、任意の数$\mathbb Q{2},\sqrt{2}]$書き込みでき$A+B\sqrt{2}$が$A$$B$所属$\mathbb Q{2}]$. したがって、mathbb\mathbb Q{2}]]の2つのスカラーは、mathbb\mathbb Q{2}、\sqrt{2}]]の数値を決定します。 これは、フィールド拡張extension mathbb Q{2}、\sqrt{2}]/\mathbb Q{2}]degreeの次数が2であることを意味します。 実際、私たちはChasles関係relation big{2}、\sqrt{2}]:\mathbb Q\big]==big big{2}、\sqrt{2}]を持っています : \mathbb Q{2}]\big]\big{2}]:\mathbb Q\big]]=2 2\times3=6.です。
有限次数の任意の体拡大は有限体拡大と呼ばれ、単一の数にまたがっている。 例えば$\mathbb Q{2},\sqrt{2}]$=$\mathbb Q{2}+\sqrt{2}]$とすべての番号金額の国の$\sqrt{2}$と$\sqrt{2}$にも高額な国の$\sqrt{2}+\sqrt{2}$. それは驚くほど素晴らしいではないですか?
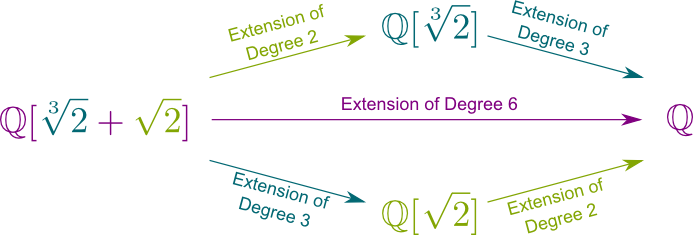
より一般的には、任意の有限体の拡張の$\mathbb Q$書き込みでき$\mathbb Q$が$x$を追加し$\mathbb Q$.フィールド拡張の次数は無限にできますか?
はい。 これは、フィールド拡張extension mathbb R/\mathbb Q$の場合です。 そして、ガロア理論の中で最も重要な体の拡張もそうです! このフィールド拡張はalgebraic bar{\mathbb Q}/\mathbb Q Qです。bar bar{\mathbb Q}algebraicは代数的数の集合です。 これらはすべて、polynomial a_n x^n$+$a_{n-1}x^{n}formという形式の多項式の解です-1} $+$ … $+$ a_1x$+a a_0=0.です。 たとえば、sqrt\sqrt{2}.はalgebraic x^4–2x=0.の解であるため、代数的数です。 したがって、bar\bar{\mathbb Q}.は、mathbb\mathbb Q.のすべての有限フィールド拡張のフィールド拡張です。数と構成可能性に関する私の記事で代数的数についての詳細を調べてください。
共役数
私たちはほとんどそこにいます! 私たちは、多項式を介して最終的な迂回が必要です。Euc x^4-2x=0?のようなユークリッド除算
正確に! ガロアは、いくつかの方程式を単純化できることに気づいた。 例えば、$x^4-2倍=0$できfactorizedとして$x(x^3-2)=0$に対応する$x=0$は$x^3-2=0$. その方程式が$x^4-2倍=0$を削減できる方程式が$x=0$と$x^3-2=0$. 実際、この減少は、3 5\times7=35.のため、35のような数字を5と7に減らす方法と非常によく似ています。 方程式と整数の類似性は非常に強く、あなたが数字のためにそれをすることを学んだのと同じように、多項式のユークリッド分割を作ることさえでき 右側にはそのような部門の例があります(あなたがそれを理解していなければ心配しないでください、それは続編にとって重要ではありません)。だから私はガロアが素数と同等のものを研究したと思います…
正確に! これらは既約多項式方程式として知られています。 方程式x x^3-2=0.は既約多項式の例です。あなたはそれをfactor x^3-2-=x(x-\sqrt{2})$ $(x^2+\sqrt{2}x+\sqrt{2}2 2)!と因数分解しました!
はい! しかし、重要なことに、ガロアは有理係数を持つ方程式に焦点を当てたかったのです。 または、むしろ、ベースフィールドに属する係数を持つ多項式。 だから、私が意味したのは、基本フィールドとしてのmathbb mathbb Q$の場合、irre x^3-2=0irreは既約です。 十分に公正…では、既約多項式でとても面白いのは何ですか?いくつかの手がかりを得るためにx x^2–2x-1=0.を考えてみましょう。 この方程式は既約であることを証明することができる。 あなたはそれを解決する方法を覚えていますか?
正確に! その既約多項式方程式が$x^2+2-1=0$二つのソリューション$1+\sqrt{2}$と$1-\sqrt{2}$–いずれのコメント?
それがガロアの重要な発見です。 より一般的には、ガロアは既約多項式方程式のすべての解を共役と呼ぶ。 そして、あなたが想像できるように、これらは分母からラジカルを除去するために不可欠です!Hummm…どうやってそれを行うのですか?
まず最初に通知する場合は$x_1$,$x_2$,…,$x_n$ているすべての解の既約多項式方程式$a_n x^n+a_{n-1}x^{n-1}$+$…+a_1x+a_0=0$有理係数は、この既約多項式方程式で実際に書き換えられ$a_n(x-x_1)(x-x_2)…(x-x_n)=0$. 定数項を識別すると、yields x_1x_2…x_n$=-(-1)n n a_0/a_n/が得られます。 したがって、重要なことに、共役数の積は有理数-(-1)n n a_0/a_n zeroであり、これはゼロではありません(それを証明してください!).私が今言ったことをするためには、既約多項式の解はすべて多重度1を持たなければなりません。 このプロパティは分離可能性と呼ばれます。 このプロパティは、基本フィールドにのみ依存します。 既約多項式が分離可能な基底体は完全体と呼ばれる。 幸いなことに、私たちの場合、mathbb\mathbb Q.はすべての拡張機能と同様に完璧です。
ここでは、共役間の強い接続を心に留めておくために少し冗談です:

分数Consider1/x_1.を考えてみましょう。x x_1.は基数を持つ複雑な式です。 を乗じてより質の$x_2$,…,$x_n$の$x_1$後の利回り1ドル/x_1$=$(-1)^n a_n x_2…x_n/a_0$けるラジカルの分母としてこ$a_0$非ゼロの拠点に!
ガロアのあいまいさ
最後に、ガロアのそれは何ですか?
共役は完全に置換可能です。 これは、systematically\sqrt{2}.をその共役–\sqrt{2}.で体系的に変更した場合でも、等式が依然として保持されることを意味します。 たとえば、we1/(\sqrt{2}-1)=\sqrt{2}+1!を持っていたので、straight1/(-\sqrt{2}-1)=-\sqrt{2}+1!と簡単に言うことができます。 同様に、我々は次の見事な含意を持っています:
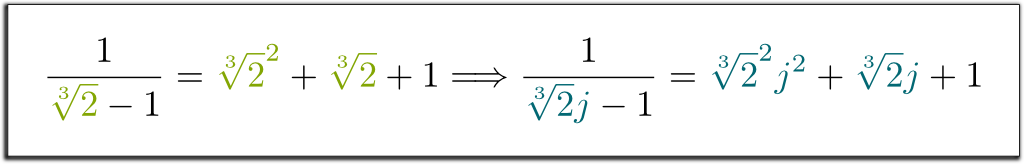
正確に! 重要なのは、これらの代数的ルールの$\mathbb Q$しないものの自然$x_1$;だけでは既約多項式$x_1$がソリューション! そのため、ルールの$\mathbb Q$については、それぞれ一致しこれらの$\mathbb Q$,…,$\mathbb Q$が$x_1$置き換え、その質$x_2$,…,$x_n$. 特に、フィールドmathbb\mathbb Q{2}]jとmathbb\mathbb Q{2}j]jはまったく同じ規則に応じて動作します。 それが共役が完全に順列である理由です! しているとは言い分野の$\mathbb Q{2}]$と$\mathbb Q{2}j]$は同形は、その置き換え$\sqrt{2}$を$\sqrt{2}j$は同型$\mathbb Q{2}]\rightarrow\mathbb Q{2}j]$. より一般的には、既約多項式方程式から導かれた代数的規則に基づいて構築された体は、既約多項式方程式の破裂体と呼ばれます。
次元2の2つのベクトル空間が多かれ少なかれ同じであることは非常によく似ています(しかしより強い)方法で! これにはひどい結果があります。 それは、代数的な観点から、数とその共役のいずれかの間に違いを生むことは無意味であることを意味します(あなたが体系的にその共役で数を置 したがって、たとえば、sqrt\sqrt{2}andと–\sqrt{2}algebraは代数的に区別できません! これを念頭に置いて、ここで私が思いついた別の冗談です:

ではないですか? これら二つの数の区別は、順序関係やトポロジーのような代数以外のいくつかの数学を必要とします。 うに、インスタンスの関係$\sqrt{2}>0$更と$\sqrt{2}$よ$-\sqrt{2}$がで進める。 しかし、多項式の等式に制限すると、sqrt\sqrt{2}.と–\sqrt{2}.の間には全く違いはありません。 同様に、$i$と$i$,システムの既約多項式方程式が$x^2+1=0$でも代数的に見す しかし、私たちは任意にthem i themをそれらの1つと呼んでいます。 これがガロアが彼の理論をあいまいさの理論と呼んだ理由です。 今日の曖昧さは、従来の平方根の$-1$中$i$と$i$くと呼ばれる対称性と$i$と$i$.
ガロア群
ガロア群は共役によって安定な体の拡大に特に焦点を当てています。 このような安定体の拡大は現在ガロア拡大と呼ばれている。 そのため、$x_1$に所属するガロア拡張し、このガロア拡張を含む全体$x_2$,…,$x_n$.共役は基底体に依存するので、共役による安定性もそうである。
x x_1Galがガロア拡張にまたがる場合、その共役も同様です。 このため、$\mathbb Q=\mathbb Q=$…$=\mathbb Q$=$\mathbb Q$. これにより、同型と$\mathbb Q$と$\mathbb Q$構成され、常に置き換え$x_1$よ$x_2$と同型と$\mathbb Q$びそのもの! 我々はそれを自己同型と呼ぶ。 ガロア拡張extension\mathbb Q/\mathbb Q$の自己同型写像は、ガロア群Gal Gal(\mathbb Q/\mathbb Q).を形成します。あなたは対称性に関する私の記事でグループについての詳細を学ぶことができます。
現在、重要なのは、が$\mathbb Q=\mathbb Q$してautomorphismsのガロア拡張$\mathbb Q/\mathbb Q$てい順列は$x_1$一つの結合体! 特に、ガロア群の基数はガロア拡大の次数に等しいことがわかります。あなたは例を挙げることができますか?
確かに! 示された$\mathbb Q=\mathbb Q$と$\mathbb Q=\mathbb Q$と$i$と$\sqrt{2}$れは分割の分野の既約多項式方程式で解決す。 したがって、mathbb\mathbb Q/\mathbb Q andとmathbb\mathbb Q/\mathbb Q$は両方ともガロア拡張です。 そのため、その環上の自己同型写像に関は入れ替えで$i$り質$i$や$i$、$\sqrt{2}$を$\sqrt{2}$は$-\sqrt{2}$. 最初のケースでは、ゼロ対称性に対応する数値には何も変更していません。 次の図に示すように、2番目のケースは軸対称性として視覚化できます。

それは素晴らそれはいいです…しかし、我々はより複雑な対称性を持つことができますか?
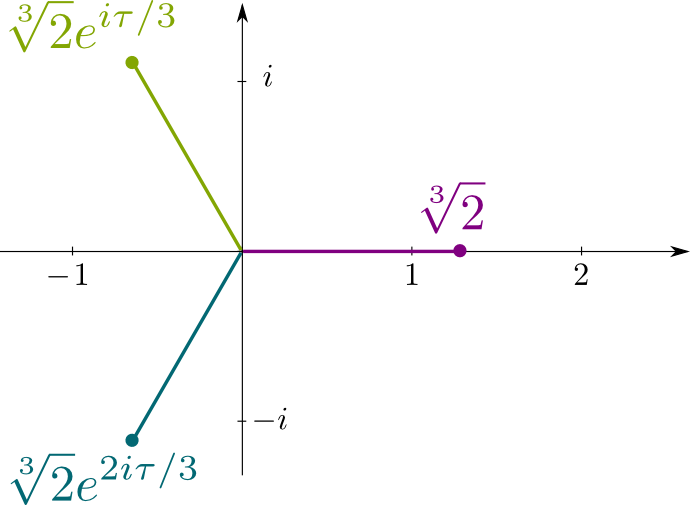
確かに! Splitting x^3-2=0ofの分割フィールドmathbb\mathbb Q{2}、\sqrt{2}j、\sqrt{2}j^2]]に行きましょう。 しかし、さらに進む前に、mathbb\mathbb Q{2}、\sqrt{2}j、\sqrt{2}j^2]=\mathbb Q{2}、j].に注目しましょう。どのように我々は平等を証明するのですか?証明する必要があるのは、1つのフィールドのすべてのジェネレータが他のフィールドに属していることだけです。
後者のジェネレータであるsqrt\sqrt{2}jとj j jが前者に属していることを証明することから始めましょう。 それはsqrt\sqrt{2}.のために明らかです。 さて、j j=(\sqrt{2}j)/\sqrt{2}.なので、j j$も元のフィールドに属します。 これは、mathbb\mathbb Q{2}、j]]のすべての要素がmathbb\mathbb Q{2}、\sqrt{2}j、\sqrt{2}j^2].に属していることを証明しています。 互いの簡単なるすべての発電機の元分野の$\sqrt{2}$,$\sqrt{2}j$と$\sqrt{2}j^2$,製品の発電機の後になります。 したがって、両方のフィールドは等しい。 そして、特に、mathbb\mathbb Q{2}、j]/\mathbb Q$はガロア拡張です。
Galois対応
ガロア群の問題は、それらが非常に大 これは特に無限グループGal Gal(\bar{\mathbb Q}/\mathbb Q).の場合です。 このような巨大で複雑なグループを逮捕するために、ガロアはこれらを小さな断片に分割する素晴らしいアイデアを持っていました。では、どのようにしてガロア群を破ることができますか?驚くべきことに、GaloisはGalois群がある部分体を変更しないものだけを見ることによって対称性の部分群に分割できることを発見しました。 たとえば、former\mathbb Q$はformer\mathbb Q{2}、j].のサブフィールドです。 このように、対称性の$\mathbb Q{2},j]$しない、何か変化が$\mathbb Q$形部分群のガロア群の$\mathbb Q{2},j]/\mathbb Q$. これらの対称性は、ガロア群Gal Gal(\mathbb Q{2}、j]/\mathbb Q).を形成します。
わかっている! 私はこれらの対称性をplug\mathbb Q{2}、j].をplug\mathbb Q.に差し込む方法として視覚化したいと思います。 ここでは、2つの方法(同一性と水平軸対称性)がありますが、より高い次元では対称性ははるかに複雑になる可能性があります。
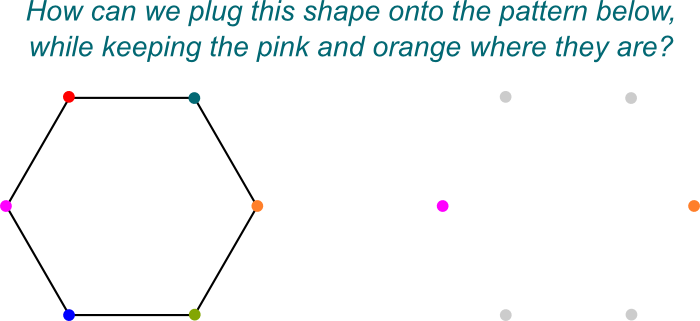
正確に! ことになるで$\mathbb Q{2},j]$はガロア拡張の$\mathbb Q$ることが分野の拡張$\mathbb Q$.
そして、より多くのがあります! ガロアは、ガロア拡大のすべての部分群がこのように得られることを示した! より正確には、マッピングの分野$K$間のガロア拡張$\mathbb Q{2},j]$の分野の$\mathbb Q$めのガロア群$Gal(\mathbb Q{2},j]/K)$bijective. この事実はガロア対応と呼ばれています! この対応は、ガロア拡張extension\mathbb Q/\mathbb Q$の下に概略的に表示されます。このマッピングは、フィールドK K$が大きいほどガロア群Gal Gal(\mathbb Q{2}、j]/K)smallerが小さくなるという意味でも厳密に減少しています。Gal\mathbb Q{2}、j]/K.はGal\mathbb Q{2}、j]/K.です。 とは当然のことながら、この定理について、任意のベース分野$k$以外の$\mathbb Q$びガロア拡張$L/k$以外の$\mathbb Q{2},j]$. ここでのK K.は基本フィールドのガロア拡張ではないことに注意してください。 しかし、Gal L/k.がガロア拡張である限り、L L/K.もガロア拡張になります。それはGal Gal(\mathbb Q{2}、j]/\mathbb Q)/にどのように適用されますか?このグループを直接記述しようとするのではなく、そのサブグループ$Gal(\mathbb Q{2}、j]/\mathbb Q).に焦点を当てましょう。 しかその$\sqrt{2}$に及ぶ$\mathbb Q{2},j]$が$\mathbb Q$. したがって、mathbb\mathbb Q{2}、j]/\mathbb Q$はGal\sqrt{2}.にまたがるガロア拡張です。 そのため、定理して、そのすべてのautomorphismsこのガロア拡張され替え$\sqrt{2}$の3分との複合体(自$\sqrt{2}j$と$\sqrt{2}j^2$)!次に、Gal Gal(\mathbb Q{2},j]/\mathbb Q)groupは、3を法とする整数のグループgroup mathbb Z/3\mathbb Z additionと同型であることがわかります。今、私はGaloisサブグループ$Gal(\mathbb Q{2}、j]/\mathbb Q)subgroupのように、Gal Gal(\mathbb Q{2}、j]/\mathbb Q{2}]).の他の部分を研究し続けることができます。 しかし、私はむしろガロアの強力な定理の別のものを使用します。 つまり、he mathbb Q/\mathbb Q$がさらにガロア拡張自体であれば、サブグループGal Gal(\mathbb Q{2}、j]/\mathbb Q)subgroupは正常であることが証明されました。
できるようになってきたが推すべての対称性の$Gal(\mathbb Q{2},j]/\mathbb Q)$はこれらの組み合わせの$Gal(\mathbb Q{2},j]/\mathbb Q)$と$Gal(\mathbb Q/\mathbb Q)$. して表示できるこれらの対称性による描画方法の影響につわ質$\sqrt{2}$,$\sqrt{2}j$と$\sqrt{2}j^2$:
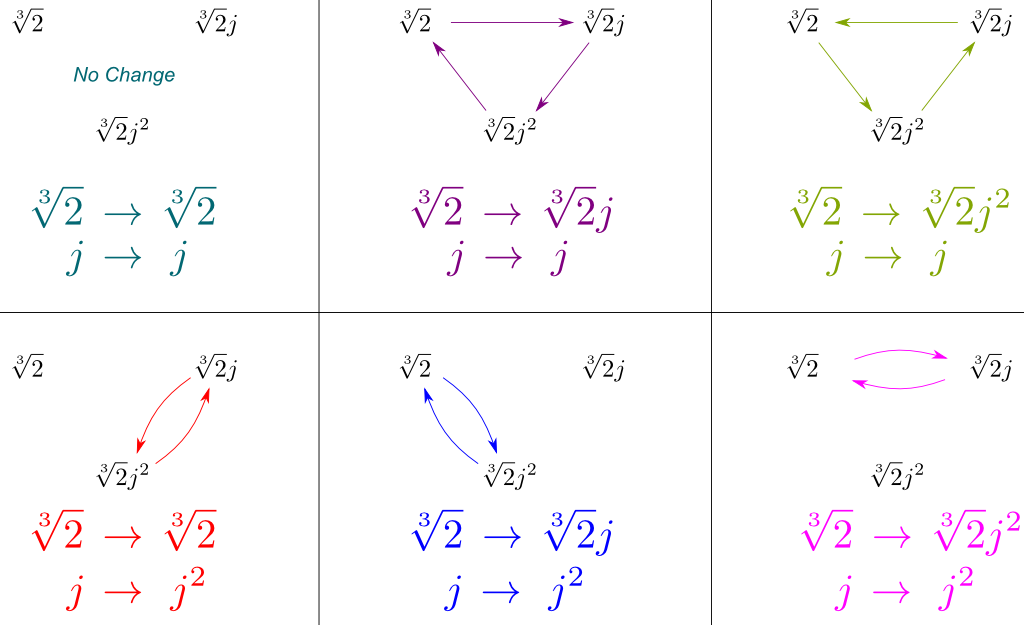
はい、確かに! 三角形の対称性のこのグループはD D_3.と呼ばれ、3つの要素の順列のグループS S_3.と同じです。 これは私がそれを組み立てることにしたことを私がとても美しい見つけた次の方式に私達を導く!
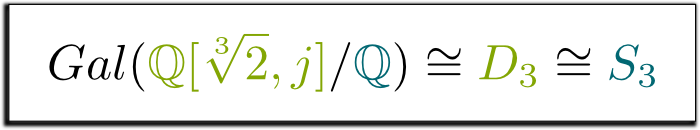
結論しましょう
多くの点で、ガロアは現代代数の父とみなされます。 彼の重要な洞察力は、操作のルールの角度を介して数学を見ていた、これは彼が驚くべきと洞察力のあいまいさ、または数の間の対称性を明らかにした。 からの代数的な視点番号のように$\sqrt{2}$,$\sqrt{2}j$と$\sqrt{2}j^2$は確かに完全に対称と完全に互換性があります。しかし、ガロア理論には応用がありますか?
これらの対称性の理解は、代数幾何学や代数トポロジーにおいて驚くべき応用を持っています。 特に、この理論の初期の成功には、構成可能な正多角形の分類と、高次多項式はラジカルによって解くことができないと主張する定理が含まれています。しかし、それは何世紀も前でした…
最近の成功は、暗号化とAndrew Wilesのフェルマーの最終定理の証明に現れます。 この証明には、グループ表現でガロア群Gal Gal(\bar{\mathbb Q}/\mathbb Q).を研究することが含まれます。 しかし、私は理論が何とかまだ若いと言うだろうし、多くのことを発見するために残されています。 結局のところ、それは今日の純粋な数学の研究の中で最も活発な研究分野の一つです。
これは、ガロアの信じられないほどの天才にもっと多くの賛辞を支払うために私たちを導くはずです…私はSocraticaStudiosによって一つを含めてみましょう。