Introduction

有効な集団サイズ(Ne)は、集団における遺伝的ドリフトの量を推定する重要な遺伝的パラメータであり、研究中の集団と同じ値をもたらすことが期待される理想化されたWright-Fisher集団のサイズとして記述されている(Crow and Kimura,1970)。 Ｎｅサイズは，国勢調査人口サイズ（Ｎ ｃ）の変動，繁殖性比および生殖成功の分散によって影響され得る。

Ne推定は、人口統計学、血統ベース、またはマーカーベースの三つの方法論的カテゴリーに分類されるアプローチを用いて達成することができる（Flury et al., 2010). 血統データは伝統的に家畜のNe推定値を得るために使用されてきました。 しかし、Neの信頼できる推定値は、血統が完了していることに依存します。 この知識の状態は、十分に多くの世代にわたって人口統計学的パラメータが正確に監視されているいくつかの国内集団で実現可能である。 しかし、実際には、このアプローチの適用性は、高度に管理された品種を含むいくつかのケースに限定されたままである（Flury et al. 2010年、Uimari and Tapio、2011年）。

不完全な血統の制限を克服するための一つの解決策は、ゲノムデータを使用してNeの最近の傾向を推定することです。 いくつかの著者は、連鎖不平衡（LD）に関する情報からNeを推定することができることを認識している（Sved、1971; ヒル、1981）。 ＬＤは、ゲノム中の遺伝子座の物理的位置間の組換え速度の関数として、異なる遺伝子座における対立遺伝子の非ランダムな会合を記述する。 しかし、ＬＤシグネチャは、混和および遺伝的ドリフト（Ｗｒｉｇｈｔ、１ ９ ４ ３；Ｗａｎｇ、２ ０ ０ ５）などの人口統計学的プロセスから、または選択的掃引中の「ヒッチハイク」（Ｓｍｉｔｈ ａｎｄ Ｈ Ａｉｇｈ、１ ９ ７ ４）または背景選択（Ｃｈａｒｌｅｓｗｏｒｔｈ ｅ ｔ ａ ｌ．, 1997). このようなシナリオでは、異なる遺伝子座の対立遺伝子は、ゲノム内のそれらの近接性とは無関係に関連するようになる。 集団が閉鎖的で汎関数的であると仮定すると、中性のリンクされていない遺伝子座の間で計算されるLD値は、遺伝的ドリフトに排他的に依存する（Sved、1971;Hill、1981）。 この発生は、ＬＤの分散（対立遺伝子頻度を用いて計算される）と有効集団サイズとの間の既知の関係に起因して、Ｎｅを予測するために使用され得る（Ｈｉｌｌ、１ ９ ８ １）。

ジェノタイピング技術の最近の進歩（例えば 数万のＤＮＡプローブを有するＳＮＰビーズアレイを使用して）は、家畜およびヒトのＮｅを推定するのに理想的な膨大な量のゲノム全体の連鎖データの収集を可能にした（例えば、Ｔｅｎｅｓａ ｅ ｔ ａ ｌ． 2007年度デRoos et al. ら、２ ０ ０ ８；Ｃｏｒｂｉｎ ｅ ｔ ａ ｌ． ら，２ ０ １ ０；ＵｉｍａｒｉおよびＴａｐｉｏ，２ ０ １ １；Ｋｉｊａｓら．, 2012). しかし、LDからNeの推定を可能にするソフトウェアツールは欠けており、研究者は現在、データを操作し、LDを推測し、適切な計算を実行し、Neを推定するためにオーダーメイドスクリプトを使用する傾向があるツールの組み合わせに依存している。

ここでは、サンプルサイズ、フェージング、再結合速度を補正するSNPデータを使用して、世代間のNe傾向を推定できるソフトウェアツールSNePについて説明し

材料と方法

SNePがLDを計算するために使用する方法は、段階的なデータの可用性に依存します。 位相が既知である場合、ユーザは、遺伝子座の各対の間のＬＤを定義するためにハプロタイプ頻度を利用するｈｉｌｌ ａｎｄ Ｒｏｂｅｒｔｓｏｎ（１ ９ ６ ８）２乗相関係数を選択することができる（式１）。 しかし、既知の位相がない場合には、遺伝子座の対の間の二乗ピアソンの積-モーメント相関係数を選択することができる。 これらの２つのアプローチは同じではないが、それらは非常に匹敵する（Ｍｃｅｖｏｙ ｅ ｔ ａ ｌ．, 2011):2π i=1n(Xi−X)2π i=1n(Yi−Y)2(2)

ここで、pAおよびpBはそれぞれ、n個の個体について測定された二つの別々の遺伝子座（X、Y）における対立遺伝子Aおよびbの頻度であり、pABは、n個の個体について測定された二つの別々の遺伝子座（X、Y）における対立遺伝子Aおよびbの頻度である。研究された集団における対立遺伝子aおよびbを有するハプロタイプの頻度、xおよびyはそれぞれ第一および第二の遺伝子座の平均遺伝子型頻度、xiは第一の遺伝子座における個々のiの遺伝子型であり、Yiは第二の遺伝子座における個々のiの遺伝子型である。 式(2)は、ハプロタイプ頻度の代わりに遺伝子型対立遺伝子数を相関させ、二重ヘテロ接合体の影響を受けません(このアプローチは、PLINKの–r2オプションと同じ推定値をもたらします)。

SNePは、r2、Ne、およびc（再結合率）の関係（式3—Sved、1971）に基づいて歴史的な有効母集団サイズを推定し、ユーザーがサンプルサイズとゲームフェーズの不確実性の修正（式4—Weir and Hill、1980）を含めることができるようにする。:

ここで、nはサンプリングされた個々の数であり、配偶相が既知の場合はβ=2、位相が既知でない場合はβ=1である。いくつかの近似を用いて、二つの遺伝子座間の物理的距離（δ）を基準として再結合速度を推測し、それを連結距離（d）に変換するために使用され、これは通常Mb（δ）≤cM（d）として記述される。 Dの値が小さい場合は後者の近似が有効ですが、dの値が大きい場合は複数の再結合イベントと干渉の確率が増加し、さらに可能な最大再結合率が0.5であるため、マップ距離と再結合率の関係は線形ではありません。 したがって、非常に短いδを使用しない限り、近似ｄ∈ｃは理想的ではない（Ｃｏｒｂｉｎ ｅ ｔ ａ ｌ．, 2012). したがって、Haldane(1919)、Kosambi(1943)、Sved(1971)、およびSved and Feldman(1973)に従って、推定されたdをcに変換するためのマッピング関数を実装しました。 最初に、Ｓｎｅｐは、Ｄ＝ｋ δに従ってδに正比例するＳｎｐの各対についてｄを推測する（ここで、ｋは、ユーザ定義の再結合速度値である（Ｍｂ＝ｃｍのようにデフォルト値は１ ０−８である）。 次に、推定されたδの値は、ユーザが必要とする場合に利用可能なマッピング関数の１つに供され得る。

Neについて式（3）を解くと、記載されているすべての補正を含む、を使用してLDデータからNeの予測を可能にする（Corbin et al., 2012):ここで、Ｎｔは、世代前にｔ＝（２ｆ（ｃ ｔ））−１として計算された有効母集団サイズｔである（Ｈａｙｅｓ ｅ ｔ ａ ｌ． ２）、ｃｔは、マーカー間の特定の物理的距離について定義され、上記のマッピング関数で任意に調整された組換え速度であり、ｒ２ａｄｊは、試料サイズについて調整されたＬＤ値であり、α：＝｛１、２、２． したがって、より大きな組換え距離にわたるＬＤは、最近のＮｅについて有益であり、より短い距離は、過去のより遠い時間についての情報を提供する。 ビニングシステムは、特定の軌跡間距離に対するＬＤを反映する平均ｒ２値を得るために実装される。 実装されているビニングシステムでは、次の式を使用して各ビンの最小値と最大値を定義します:bimin=minD+(maxD−minD)(bi−1totbins)x(6a)

ここで、bi(Σ1)はビン(totBins)の総数のi番目のビンであり、minDおよびmaxDはそれぞれSnpとXとの間の最小距離および最大距離である。実数(λ0)xが1の場合、ビン間の距離の分布は線形であり、各ビンは同じ距離範囲を持ちます。 Xの値が大きい場合、距離の分布が変化し、最後のビンでは範囲が大きくなり、最初のビンでは範囲が小さくなります。 このパラメータを変更すると、各ビンの最終的なNe推定値に寄与するのに十分な数のペアワイズ比較を行うことができます。

サンプルアプリケーション

私たちは、LD、Bos indicus、Ovis ariesを使用して、時間の経過とともにNeの傾向を記述するために以前に使用されていた二つの公開されたデータセットでSNePをテストしました。 牛データセットのr2推定値は、GenABLEを使用して著者によって得られた(Aulchenko et al. ０ １を使用し、Ｈａｌｄａｎｅのマッピング関数を使用して再結合速度を調整する（Ｈａｌｄａｎｅ，１ ９ １ ９）。 ヒツジデータのr2推定値は、PLINK-1.07を用いて著者らによって計算された（Purcell et al. 2007）、MAF<0.05であり、それ以上の修正はありません。 両方の常染色体データセットについて、r2は、β=2の式（4）を使用してサンプルサイズを補正した推定値を推定します。 これらの比較分析のために、SNePコマンドラインには、遺伝子型数およびSNePの新規ビニング戦略の使用によって計算されたr2推定値とは別に、公開されSNePはc++で開発されたマルチスレッドアプリケーションであり、最も一般的なオペレーティングシステム（Windows、OSX、Linux）用のバイナリはhttps://sourceforge.net/projects/snepnetrends/からダウ バイナリには、ここで説明されているように、Neの傾向を推測するためのSNePの段階的な使用を説明するマニュアルが添付されています。 SNePは、Neを推定するために使用された各ビンについて、次のことを示すタブ区切りの列を持つ出力ファイルを生成します：ビンが対応する過去の世代 のＳｎｐの各ペア間の平均距離、平均ｒ２およびビン内のｒ２の標準偏差、およびビン内のｒ２を計算するために使用されるＳｎｐの数である。 このファイルは、Microsoft Excel、Rまたは他のソフトウェアに簡単にインポートして結果をプロットすることができます。 ここに示されているプロット(図1、3)は、出力ファイルからの世代前とNeの列に対応しています。 R2標準偏差を持つ列は、ユーザーが各ビンのNe推定値の分散、特に古い時間推定値を反映し、r2を推定するために使用されるSnpの数が小さくなると信頼性が低いビンに対して検査するために提供されています。

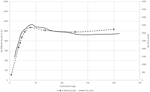
図1。 Burren et al.による六つのスイスの羊の品種のNe傾向の比較 （2014年）（破線）とこの作品（実線）。入力ファイルに必要な形式は、標準のPLINK形式（pedおよびmapファイル）です（Purcell et al., 2007). SNePを使用すると、ユーザーは上記のようにデータ上でLDを計算するか、または式（5）を使用してNeを推定するためにカスタム事前計算されたLD行列を使用す

ソフトウェアインターフェイスは、ユーザーが分析のすべてのパラメータ、例えば、bp内のSnp間の距離範囲、および分析で使用される染色体のセット（例えば、20-23）を制御することを可能にする。 さらに、SNePにはMAFしきい値を選択するオプションが含まれています(デフォルトは0です。ＭＡＦを考慮すると、サンプルサイズに関係なく不偏ｒ２推定値が得られることが示されているので（Ｓｖｅｄ ｅ ｔ ａ ｌ．，２ ０ ０ ５）、ＭＡＦを考慮すると、試料サイズに関係なく不偏ｒ２推定値が得られる。, 2008). SNePのマルチスレッドアーキテクチャは、大規模なデータセットの高速計算を可能にします(我々は、単一の染色体のために-100K Snpまでテストしました),例えば、ここで説明されているBOSデータは、2’43″で一つのプロセッサで分析されました,二つのプロセッサの使用は、1’43″に時間を短縮しました,4つのプロセッサは、1’05″に分析時間を短縮しました.

Zebuの例

Zebuの解析では、SNePで得られたNe曲線の形状とその公表されたデータ傾向は、150世代前までは滑らかな減少で同じ軌道を示し、40世代前まではピークで拡大し、最新の世代では急激な減少に終わった（図1）。 しかし、両方の曲線の傾向は同じでしたが、二つのアプローチは異なるNe推定値をもたらし、SNePの値は元の論文の値よりも約三倍大きくなりました。 我々は我々の分析で著者のパラメータを使用しようとしたが、いくつかの違いは避けられなかった、すなわち、SNePで実装されたものとは異なるアプローチでr2を推定した牛のデータの元の出版物。 SNePによる分析は遺伝子型に基づいていたが、元の分析は推定された二つの遺伝子座ハプロタイプに基づいていたため、公開されたデータは最小距離で0.32の予想r2を示し、推定値は0.23であった。 同様に、Ｍｂｏｌｅ−Ｋａｒｉｕｋｉ ｅ ｔ ａ ｌ． (2014)は、同じ距離での推定値は0であったが、背景レベルr2=0.013約2Mbを得た。0035(データは図示せず)。 その結果，ＬＤの推定値はＭｂｏｌｅ-Ｋａｒｉｕｋｉらよりも一貫して小さかった。 (2014)我々のNe推定値はより大きくなるはずであると予想される。 この観測では、パラメータとそのしきい値を慎重に選択することの重要性を強調していますが、Ne値の絶対的な大きさは異なりますが、傾向はほぼ同

Swiss Sheepの例

SNePで分析した六つのSwiss sheepの品種は、元の論文（図2）と同等の結果をもたらし、主にNeトレンド曲線が重複していました（図3）。 しかし、Neの一般的な傾向は現在に向かって減少を示した。 SNePは、より遠い過去（700-800世代）のNeのわずかに大きな値を生成しました。 これは、SNePで使用される異なるビニングシステムによるものであり、ユーザーは各ビン内のペアワイズ比較のより均一な分布を得ることができます（すな、各ビン内のＳＮＰ対比較の数は、同等である）。 400世代前を超えた期間については、Burren et al. (2014)では、分析に3つのビン(400、667、および2000世代前を中心とする)のみを使用していましたが、同じ時間スパンでSNePは5つのビンを使用し、式6a、bで定義された範囲に依存するペアワイズ比較の数を使用しました。 したがって、より少ないビンの使用は、各ビン内のより小さな値のＮｅの存在を増加させる傾向があり、その結果、各ビンの平均Ｎｅ値を低下させる。 最近の過去のNe値は、過去の第29世代と比較して、非常に類似した結果をもたらした。 最大の差（50）は、SBSの品種のために得られました。

図2

図2。 この研究における第29世代で計算された最近のNe値とBurren et al. （2014年）スイスの六つの羊の品種のために。

図3

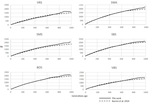
図3。 Mbole-Kariuki et al.によって得られたSHZデータにおける最後の250世代のNe傾向の比較。 (2014)(破線)とSNeP(実線)を使用しています。LDデータを用いたNeの分析は、40年前に初めて実証され、適用、開発、改善されてきました（Sved、1971;Hayes et al. ら、２ ０ ０ ３；Ｔｅｎｅｓａ ｅ ｔ ａ ｌ． 2007年度デRoos et al. ら、２ ０ ０ ８；Ｃｏｒｂｉｎ ｅ ｔ ａ ｌ． ら、２ ０ １ ２；Ｓｖｅｄ ｅ ｔ ａ ｌ．, 2013). SNPチップは非常に多くのSnpを含み、短時間で合理的な価格で入手できるため、従来は分析されたSnpの数が少ないことはもはや制限ではありません。 これは、ヒトに適用されている方法の使用を促進している（Tenesa et al. ら、２ ０ ０ ７；Ｍｃｅｖｏｙ ｅ ｔ ａ ｌ． ら、２ ０ １ １）ならびにいくつかの家畜化種（Ｅｎｇｌａｎｄ ｅ ｔ ａ ｌ． ら、２ ０ ０ ６；ＵｉｍａｒｉおよびＴａｐｉｏ、２ ０ １ １；Ｃｏｒｂｉｎ ｅ ｔ ａ ｌ． ら、２ ０ １ ２；Ｋｉｊａｓ ｅ ｔ ａ ｌ．, 2012). これらの改善に伴い、方法論的限界が明らかになり、ここで対処されており、努力の大部分は最近のNeの正しい推定を指しています。 しかし、推定値の定量的値は、サンプルサイズ、LD推定のタイプ、およびビニングプロセスに大きく依存する（Waples and Do、2008;Corbin et al.,2012),その定性的なパターンは、データ操作よりも遺伝情報に多く依存していますが、.

これまでのところ、この方法はさまざまなソフトウェアを使用して適用されており、結果をビンにする標準化されたアプローチは存在せず、各研究,2012),各ビンの一定の範囲を持つ距離クラスのビニング(Kijas et al.,2012)または線形の方法で距離クラスごとのビンニングが、より最近の時間点のためのより大きなビンを持つ(Burren et al., 2014). 我々の知る限りでは、LDを通してNeを推定する唯一のソフトウェアはNeEstimatorである（Do et al. 2014年）、旧LDNEのアップグレード版（Waples and Do、2008年）では、大きなデータセット（50k SNPChipとして）の分析を可能にしている。 SNePは歴史的なNeの傾向を推定することに焦点を当てているが重要なのは、NeEstimatorの目的は、現代の公平なNeの推定値を生成することですが、LDを通じて人口統計を調査しながら、後者は、したがって、補完的なツールとして考慮されるべきである。

SNePを使用して、この方法が以前に適用された二つのデータセットを分析しました。 ヒツジのデータについて得られた結果は，Ｂｕｒｒｅｎらによって得られた結果と定量的および定性的に同等であった。 (2014)、Zebuデータについては、Mbole-Kariuki et al. (2014)Neの我々のポイント推定値は、データのために記載されたものよりも大きかったが(Mbole-Kariuki et al., 2014). これら二つの結果の間の不一致は、BurrenらがSNePによってr2を推定するために使用されたのと同じアプローチを使用するPLINK（大規模なSNPデータ操作のための標準ソフトウェア）を使用してr2推定値を生成したことを反映しているが、Mbole-Kariuki et al. その後、Hao et al. (2007)r2推定のために. LDに異なる推定値を使用することは、Ne曲線の定量的側面にとって重要であり、Neとr2の双曲線相関のために、0に近い範囲でのr2の減少はNe推定値の非常に大きな変化をもたらす可能性があるが、r2値が高い場合、すなわち1に近い場合、推定値の差はあまり有意ではない。 したがって、いずれかのデータセットではＮ ｅ値は実質的に異なるが、いずれの場合もＮ ｅ曲線は最初に公開されたものと重複していた。

すでに他の著者によって示唆されているように、この方法で得られた定量的推定値の信頼性は、特に最新および最古の世代に関連するNe値（Corbin et al. 最近の世代では、cの大きな値が関与しており、Hayesが時間の経過とともに変数Neを推定することを提案した理論的な意味に適合していないため（Hayes et al., 2003). 最も古い世代の推定値は、合体理論が過去に4NE世代の後にSNPを確実にサンプリングすることができないことを示しているため、信頼できない可能性があります(Corbin et al., 2012). さらに、Ne推定値、特に過去の世代に関連する推定値は、MAF値やアルファ値の選択などのデータ操作因子によって強く影響されます。 さらに、適用されるビニング戦略は、例えば、各ビンを移入するためにペアワイズ比較の数が不十分である場合、方法の一般的な精度を妨げる可能性が

方法のアプリケーションの一つは、品種の人口統計を比較することです。 この場合、Ne曲線の形状は、その品種または種の潜在的な人口統計学的指紋としてそれらを使用することによって、数値よりも異なる人口統計学的履歴を区別するための最適なツールであるが、突然変異、移動、および選択がLDを通じてNe推定に影響を与える可能性があることを考慮に入れている（Waples and Do、2010）。 さらに、SNeP（およびNeを推定するための他のソフトウェア）で分析されたデータを慎重に検討することは、混合物などの交絡因子の存在がNeの偏った推

SNePの目的は、より一貫した方法で高スループット遺伝子型データを使用してNeを推定するためにLD法を適用するための高速かつ信頼性の高いツールを提 これにより、2つの異なるr2推定アプローチに加えて、外部ソフトウェアからのr2推定を使用するオプションが可能になります。 SNePの使用は、この方法の限界とその背後にある理論を克服するものではありませんが、ユーザーはこれまでに提案されたすべての修正を使用して理論を

著者の貢献

MBは、ソフトウェアと原稿を考案し、書きました。 MB、MT、およびPOtWは、ソフトウェアをテストし、分析を実行しました。 MT、POtW、MWBは原稿を改訂しました。 すべての著者が最終原稿を承認しました。

利益相反に関する声明

著者らは、この研究は、利益相反の可能性と解釈される可能性のある商業的または財政的関係がない場合に行われたと宣言している。

謝辞

私たちは、羊のデータを提供し、有用な議論のためにChristine Fluryに感謝します。 我々はまた、この論文を改善するための有用な提案のための二つのレビュアーに感謝します。 MBはプログラムマスターとバック（Regione Sardegna）によってサポートされていました。

Charlesworth,B.,Nordborg,M.,And Charlesworth,D.(1997). 細分化された集団における遺伝的多様性の平衡パターンに対する局所選択、バランスのとれた多型および背景選択の影響。 ジュネット 70号、155-174頁。 doi:10.1017/S0016672397002954

PubMed Abstract|Full Text|CrossRef Full Text/Google Scholar

Crow,J.F.,And Kimura,M.(1970). 集団遺伝学の理論を紹介します。 ニューヨーク、ニューヨーク：ハーパーと行。

Google Scholar

太田、T.、木村、M.(1971)。 有限集団における突然変異の定常流下における二つの分離ヌクレオチド部位間の連鎖不平衡。 遺伝学68,571-580.

PubMed Abstract|Full Text|Google Scholar

ライト、S.（1943）。 距離による分離。 遺伝学28,114-138.

PubMed Abstract|Full Text|Google Scholar