Prealgebra
学習成果
- 三角形の面積、底辺と高さを見つける
- 周囲と他の二つの長さを与えられた三角形の片側の長さを見つける
私たちは今、長方形の面積を見つける方法を知っています。 この事実を使用して、三角形の面積の式を視覚化するのに役立ちます。 下の長方形では、長さbと幅hというラベルが付いているので、面積はbhです。
長方形の面積は、底辺bに高さhを掛けたものです。
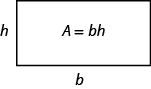
長方形は、等しい面積の二つの三角形に分割することができます。 各三角形の面積は、長方形の面積の半分です。
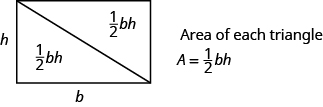三角形の面積を見つけるには、その底辺と高さを知る必要があります。 ベースは、三角形の片側の長さであり、通常は底部の側です。 高さは、ベースと反対の頂点を結ぶ線の長さであり、ベースと\text{90}circ\circの角度を作ります。 下の画像は、それぞれの底辺と高さがマークされた三つの三角形を示しています。三角形の高さhは、底辺を反対の頂点に接続し、底辺と\text{90}circ\circ角度を作る線分の長さです。
三角形の高さhは、底辺を反対の頂点に接続し、底辺と\text{90}circ\circ角度を作
m\angle{A}+m\angle{B}+m\angle{C}=180^\circ
三角形の周囲は辺の長さの合計です。
m\angle{A}+m\angle{B}+m\angle{C}=180^\circ
三角形の面積は、底辺bの半分に高さhを掛けたものです。
A=\frac{1}{2}bh
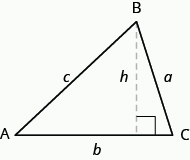
頂点にはA、B、およびcというラベルが付けられています。 三角形の頂点にある頂点Bから三角形の底辺までの垂直点線があり、直角に底辺を満たしています。 点線はhとラベル付けされています。
例
底辺が11インチで高さが8インチの三角形の面積を見つけます。
ソリューション
| ステップ1。 問題を読んでください。 図を描き、与えられた情報でラベルを付けます。/td> |  |
|
| ステップ2。 あなたが探しているものを特定します。 | 三角形の面積 | |
| ステップ3。 名前。 それを表す変数を選択します。 | ||
| ステップ4。翻訳します。
適切な式を記述します。 置換します。 |
 |
|
| ステップ5。 方程式を解く。 | A=44平方インチ。 | |
| ステップ6。 チェック：
a=\frac{1}{2}bh 44\stackrel{？}{=}\frac{1}{=}\frac{1}{2}(11)8チェックマーク |
||
| ステップ7。 質問に答えろ | 面積は44平方インチです。 |
それを試してみてください
例
三角形の庭の周囲は24フィートです。 両側の長さは4フィートと9フィートです。 第三の側面はどのくらいですか？
それを試してみてください
例
三角形の教会の窓の面積は90平方メートルです。 窓の底は15メートルです。 窓の高さは何ですか？
それを試してみてください
二等辺三角形と正三角形
直角三角形のほかに、いくつかの他の三角形は特別な名前を持っています。 同じ長さの2辺を持つ三角形は、二等辺三角形と呼ばれます。 同じ長さの三辺を有する三角形は、正三角形と呼ばれています。 下の画像は、両方のタイプの三角形を示しています。
二等辺三角形では、2つの辺の長さは同じで、3番目の辺は底辺です。 正三角形では、3つの辺の長さはすべて同じです。
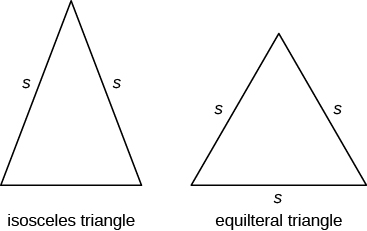
二等辺三角形と正三角形
二等辺三角形の三角形は、同じ長さの二つの辺を持っています。
正三角形は、同じ長さの三辺を持っています。
例
正三角形の周囲は93インチです。 各辺の長さを求めます。
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. スカーフは、ベースが
60インチの二等辺三角形になります。 どのくらい彼女は二つの等しい側面を作ることができますか？
