Sensor Fusion
Kalman filters
データをマージするために使用されるアルゴリズムは、カルマンフィルタと呼ばれます。
カルマンフィルターは、データ融合で最も一般的なアルゴリズムの1つです。 ルドルフカルマンによって1960年に発明され、それは今、ナビゲーションと追跡のために私たちの携帯電話や衛星で使用されています。 フィルターの最も有名な使用は月に乗組員を送り、持って来るアポロ11の代表団の間にあった。
カルマンフィルターを使用する場合はどうすればよいですか?カルマンフィルタは、現在(フィルタリング)、過去(平滑化)、または未来(予測)における動的システム(時間とともに進化する)の状態を推定するために、data fusionに使 自動運転車に組み込まれたセンサーは、時には不完全でノイズの多い測定値を放出します。 センサの不正確さ(ノイズ)は非常に重要な問題であり、カルマンフィルタによって処理することができます。
カルマンフィルタは、xで表されるシステムの状態を推定するために使用されます。div>
各推定値で、不確実性pの尺度を関連付けます。
センサーの融合を実行することにより、同じオブジェクトの異なるデータを考慮に入れます。 レーダーは歩行者が10メートル離れていると推定し、Lidarは12メートルと推定することができます。 カルマンフィルターを使用すると、2つのセンサーのノイズを排除することによって、実際に歩行者が何メートルであるかを正確に判断することができま
カルマンフィルタは、その周りのオブジェクトの状態の推定値を生成できます。 推定を行うには、現在の観測値と以前の予測のみが必要です。 測定履歴は必要ありません。 したがって、このツールは軽く、時間とともに改善されます。P>
どのように見えるか
状態と不確実性はガウスで表されます。div>



ガウスは、面積が1である連続関数です。 これにより、確率を表すことができます。 私たちは正規分布の確率にあります。 カルマンフィルターの一モダリティは、システムの状態を推定するために毎回単一のピークがあることを意味します。
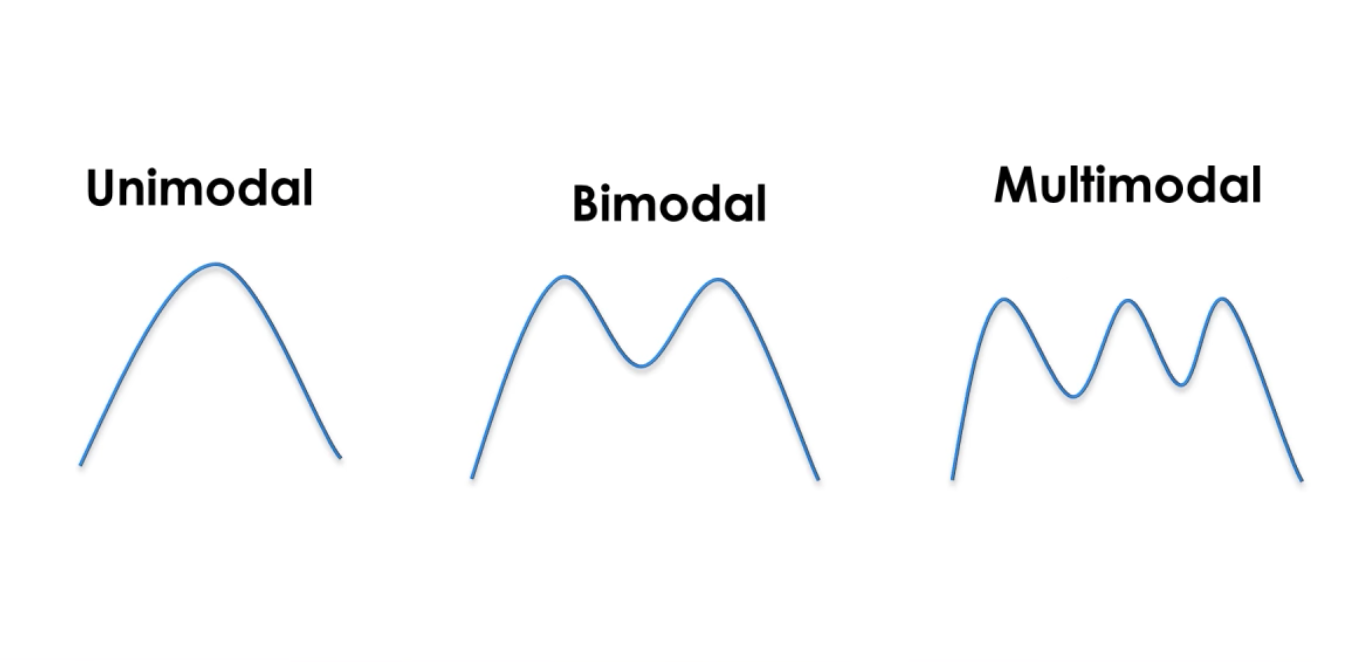
状態を表す平均σと不確実性を表す分散σ2があります。 分散が大きいほど、不確実性が大きくなります。
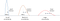
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.
Bayesian Filtering
In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: センサーの観測値を使用して予測状態を修正し、より正確な推定値を取得します。
カルマンフィルタは、推定を行うために、現在の観測値と以前の予測のみを必要とします。 測定履歴は必要ありません。P>
数学
カルマンフィルタの背後にある数学は、行列の加算と乗算で作られています。 予測と更新:私たちは、2つの段階を持っています。
予測
この予測は、時刻t-1における前の状態xおよびPから、時刻tにおける状態x’および不確実性P’を推定することからなる。P>
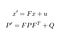
- f:t-1からtへの遷移行列
- π:ノイズが追加されました
- q: ノイズを含む共分散行列
更新
更新フェーズは、センサーからのz測定値を使用して予測を修正し、xとPを予測することで構成されます。
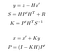
- y:実際の測定と予測の差、すなわち誤差。
- S:推定システム誤差
- H:センサーのマーカーと私たちの間の遷移の行列。
- R
- K:カルマンゲイン。 私たちの予測を修正する必要性を反映して0と1の間の係数。
R: センサーノイズに関連する共分散行列(センサーの製造元によって指定されます)。
更新フェーズでは、測定値が提供するものよりも現実に近いxとPを推定することができます。
カルマンフィルタは、事前にデータなしで、リアルタイムで予測を可能にします。 状態x(位置,速度)と不確実性Pを定義するたびに行列の乗算に基づく数学的モデルを使用した。
Représentation Prior/Posterior
この図は、カルマンフィルタで何が起こるかを示しています。P>



- 予測状態推定は、私たちの最初の推定値、私たちの予測フェーズを表します。 私たちは前について話しています。
- 測定は、当社のセンサーのいずれかからの測定です。 私たちはより良い不確実性を持っていますが、センサーのノイズは常に推定することが困難な測定になります。 私たちは可能性について話します。
- 最適な状態推定は、私たちの更新フェーズです。 今回は不確実性が最も弱く、情報を蓄積し、センサーだけよりも確実な値を生成することができました。 この値は私たちの最高の推測です。 私たちは後部について話します。
カルマンフィルターが実装するのは、実際にはベイズルールです。p>

カルマンフィルタでは、測定値から予測をループします。 我々は不確実性の尺度を維持し、定期的に私たちの予測と現実の間の誤差を計算するので、私たちの予測は、常により正確です。 行列乗算と確率式から、私たちの周りの車両の速度と位置を推定することができます。
“拡張/無香料”フィルタと非線形性
本質的な問題が発生します。 私たちの数式はすべてy=ax+b型の線形関数で実装されています。
カルマンフィルタは常に線形関数で動作します。 一方、レーダーを使用する場合、データは線形ではありません。P>



レーダーは三つの尺度で世界を見ています:
これらの三つの値は、角度φを含めると、測定を非線形にします。ここでの目標は、データθ、φ、θをデカルトデータ(px、py、vx、vy)に変換することです。
カルマンフィルタに非線形データを入力すると、結果はユニモーダルガウス形式ではなくなり、位置と速度を推定することができなくなります。


だから、我々は二つの方法に取り組んでいる理由である近似を使用します。
-拡張カルマンフィルタは、モデルを線形化するた
-Unscented Kalmanフィルターは、モデルを線形化するために、より正確な近似を使用します。
レーダーによる非線形性の包含に対処するために、技術が存在し、私たちのフィルタは、我々が追跡したいオブジェクp>