i en tid med digital verden, ser vi anbefaling i alle områder vær det er e-handel eller underholdning nettsted eller sosiale nettverk nettsteder. Anbefaling gir ikke bare brukeren sitt anbefalte valg (basert på tidligere aktivitet), men det forteller også om brukeradferd (sentimental analyse eller emotion AI).

Så først, la oss forstå hvilken anbefaling som er. Det er i utgangspunktet anbefale element til bruker basert på sin tidligere søk / aktivitet.

Figur 1 forteller Amazons anbefaling basert på tidligere nettleserhistorikk og tidligere søk. Så, vi kan si at anbefaling er i utgangspunktet forutsi fremtidig atferd basert på tidligere atferd. Det finnes to typer tilnærminger som brukes i anbefalingssystem

1-Innholdsbasert Filtrering

2-Samarbeidsbasert filtrering

Innholdsbasert Filtrering-

Det er basert på ideen om å anbefale elementet til bruker K som ligner på forrige element høyt vurdert Av K. Grunnleggende konsept i innholdsbasert filtrering ER TF-IDF (Term frequency — inverse document frequency), som brukes til å bestemme betydningen av dokument/ord / film etc. Innhold basert filtrering viser åpenhet i anbefaling, men i motsetning til samarbeids filtrering det ikke kan arbeide effektivt for store data Det Er basert På ideen om at folk som deler samme interesse i visse typer elementer vil også dele samme interesse i noen annen type elementer i motsetning til innhold basert som i utgangspunktet stole på metadata mens den omhandler virkelige liv aktivitet. Denne typen filtrering er fleksibel for det meste av domenet (eller vi kan si at det er domenefritt), men på grunn av kaldstart problem, data sparsity (som ble håndtert av matrise faktorisering) denne type algoritme står overfor noen tilbakeslag i noen scenario.Matrisefaktorisering kommer i rampelyset etter Netflix-konkurransen (2006) da Netflix annonserte en premiepenger på $1 million til de som vil forbedre sin rotmiddelkvadratytelse med 10%. Netflix ga et treningsdatasett med 100.480.507 karakterer som 480.189 brukere ga til 17.770 filmer.

Matrisefaktorisering er den samarbeidsbaserte filtreringsmetoden der matrisen m * n brytes ned i m * k og k * n . Den brukes i utgangspunktet til beregning av kompleks matriseoperasjon. Divisjon av matrise er slik at hvis vi multipliserer faktorisert matrise, får vi originalmatrise som vist i Figur 2. Den brukes for å oppdage latente funksjoner mellom to enheter (kan brukes for mer enn to enheter, men dette vil komme under tensor faktorisering)

matrix dekomponering kan klassifiseres i tre type –

1-LU dekomponering-Dekomponering av matrise I L og U matrise hvor L er lavere trekantet matrise Og U er øvre trekantet matrise, vanligvis brukt for å finne koeffisienten for lineær regresjon. Denne dekomponeringen mislyktes hvis matrisen ikke kan ha dekomponert lett

2-QR matrise dekomponering-Dekomponering av matrisen I Q og R hvor Q er kvadratisk matrise og R er øvre trekantet matrise (ikke nødvendig firkant). Brukes til egen systemanalyse

3-Cholesky Dekomponering-Dette er den mest brukte dekomponeringen i maskinlæring. Brukes til å beregne lineær minste kvadrat for lineær regresjon

Matrisefaktorisering kan brukes i ulike domener som bildegjenkjenning, Anbefaling. Matrise brukt i denne typen problem er generelt sparsom fordi det er sjanse for at en bruker kan rangere bare noen filmer. Det finnes ulike applikasjoner for matrisefaktorisering som Dimensjonsreduksjon (for å vite mer om dimensjonsreduksjon, se Curse Of Dimensionality), latent verdi dekomponering

Problemstilling

I Tabell 1 har vi 5 brukere og 6 filmer hvor hver bruker kan vurdere hvilken som helst film. Som Vi kan se At Henry ikke rate For Thor og Rocky tilsvarende Jerry ikke rate For Avatar. I virkelige verden scenario disse typer matrise kan være svært sparsom matrise

vår problemstilling er at vi må finne ut karakterer for unrated filmer som vist I Tabell 1

som vårt mål å finne vurdering av brukeren ved matrisefaktorisering, men før det må vi gå gjennom singular value decomponation (svd) fordi matrisefaktorisering og svd er relatert til hverandre /p>

SVD OG Matrisefaktorisering

før du går til dybden AV SVD, kan du først forstå Hva Som Er K og transponere (K). Hvis VI utfører PCA på matrise K(Tabell 1) får vi all brukervektoren. Senere kan vi sette disse vektorene i kolonne av matrise U, og hvis VI utfører PCA på transponere (K) får vi all filmvektoren som blir kolonne for matrise M.

Så i stedet for å utføre PCA På K og transponere(K) separat, kan VI bruke SVD som kan utføre PCA På K og transponere(K) i et enkelt skudd. SVD er i utgangspunktet faktorisert matrise K i matrise U, matrise M og diagonal matrise:

hvor k er originalmatrise, u er brukermatrise,m er filmmatrise og den midterste er diagonal matrix

for enkelhets skyld kan vi fjerne diagonal matrix for en stund, så ny ligning blir:

la r er rating definert for bruker u og element i, p er rad med m for en bruker og q er kolonnen for transponere(u) for et bestemt element i. :

merk — hvis k er tett matriseverdi enn m vil være egenvektor av k*transponere(k), tilsvarende verdi av u vil være egenvektor av transponere(k)*k men vår matrise er sparsom matrise, kan vi ikke beregne u og m ved denne tilnærmingen

så her er vår oppgave for å finne matrix m og u . En måte er å initialisere tilfeldig verdi Til M Og U og sammenligne den med originalmatrise K hvis verdien er nær K enn å stoppe prosedyren ellers minimere verdien Av U og M til De er nær K . Prosessen med denne typen optimalisering kalles gradient descent

Figur 3: gradient descent flow chart

så vår grunnleggende oppgave er å minimere den gjennomsnittlige firkantfeilfunksjonen som kan representeres som :

As our main task is to minimize the error i.e. vi må finne i hvilken retning vi må gå for at vi må skille det, derfor vil ny ligning bli

/div>

derfor blir den oppdaterte verdien for p og u nå blitt:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Basert på denne beslutningslinjen kan vi skille fordelingen av data

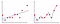
Figur 4: underfit vs overfit

i figur 2 er første plott hvor modellen er montert lineært mens den i andre plott er utstyrt med polynomgrad. Ved første blikk ser det ut til at andre plott er langt bedre enn første plott, da det gir 99% nøyaktighet på treningsdata, men hva om vi introduserer testdata og det gir 50% nøyaktighet på testdata . Denne typen problem kalles overfitting og for å overvinne dette problemet introduserer vi et konsept som kalles regularisering.Som overfitting problem er vanlig i maskinlæring, så det er to typer regularisering tilnærming som kan brukes til å fjerne overfitting

1-L1 regularization

2 – L2 regularization

L1 regularization legg lineær størrelsesorden koeffisient som straff sikt mens I L2 det legge kvadratisk størrelsesorden koeffisient til tap funksjon / feil funksjon (som diskutert ovenfor). L1 returnerer sparsomme matriser mens L2 ikke gjor det. L1 regularisering fungerer godt i funksjonsvalg i sparsom matrise.

i anbefalingsdatasett er det også store sjanser for overfitting av data. Så, for å fjerne overfitting problemet kan vi legge Til l2 regularization (som matrise er allerede sparsom vi trenger Ikke l1 regularization her) i tap funksjon derfor ny ligning av tap funksjon vil være:

div igjen kan vi finne gradient på oppdatert mse og få oppdaterte poeng ved å følge samme tilnærming som diskutert ovenfor en viktig ting å vurdere i ovennevnte scenario matrisen p og q er ikke-negativ, derfor kalles disse typer faktorisering også ikke-negativ faktorisering. Som ikke-negativ faktorisering trekker automatisk ut informasjon for ikke-negativt sett med vektor. NMF er mye brukt i bildebehandling, tekst gruvedrift, analyse av høy dimensjonale data