Prosjekt Nayuki
Definisjon: Fibonacci sekvensen er definert som \(F(0) = 0\), \(F (1) = 1\), og \(F (n) = F (n-1) + F (n-2)\) for \(n ≥ 2\). Så sekvensen(begynner med \(F (0)\)) er 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
hvis vi vil beregne en enkelt term i sekvensen (f.eks. Noen algoritmer er mye raskere enn andre.
Algoritmer
lærebok rekursiv (ekstremt langsom)
Naivt kan vi direkte utføre gjentakelsen som gitt i den matematiske definisjonen av Fibonacci-sekvensen. Dessverre er det håpløst sakte: det bruker \(Θ (n)\) stabelplass og \(Θ (φ^n)\) aritmetiske operasjoner, hvor \(φ = \frac{\sqrt{5} + 1}{2}\) (det gylne snitt). Med andre ord er antall operasjoner for å beregne \(F(n)\) proporsjonal med det endelige numeriske svaret, som vokser eksponentielt.Det bør være klart at hvis vi allerede har beregnet \(F (k-2)\) og \(F (k-1)\), så kan vi legge dem til å få \(F (k)\). Deretter legger vi til \(F (k-1)\) og \(F (k)\) for å få \(F (k + 1)\). Vi gjentar til vi når \(k = n\). De fleste merker denne algoritmen automatisk, spesielt når man beregner Fibonacci for hånd. Denne algoritmen tar \(Θ (1)\) plass og \(Θ (n)\) operasjoner.algoritmen er basert på denne uskyldige identiteten (som kan bevises ved matematisk induksjon):
\ (\left^n = \left\).
det er viktig å bruke eksponering ved å kvadrere med denne algoritmen, fordi ellers degenererer den til den dynamiske programmeringsalgoritmen. Denne algoritmen tar \(Θ (1)\) plass og \(Θ (\log n)\) operasjoner. (Merk: Vi teller antall bigint aritmetiske operasjoner, ikke ord med fast bredde.)
Rask dobling (raskere)
Gitt \(F(k)\) Og \(F(k+1)\), kan vi beregne disse:
\(\begin{align}F (2k)&= F(k) \venstre. \\F (2k + 1) &= F(k+1)^2 + F (k)^2.\end{align}\)
disse identitetene kan hentes ut fra matriseeksponeringsalgoritmen. På en måte er denne algoritmen matriseeksponeringsalgoritmen med de overflødige beregningene fjernet. Det bør være en konstant faktor raskere enn matriseutvidelsen, men asymptotisk tidskompleksitet er fortsatt den samme.
Sammendrag: de to raske Fibonacci-algoritmene er matriseutvidelse og rask dobling, hver med en asymptotisk kompleksitet av \(Θ (\log n)\) bigint aritmetiske operasjoner. Begge algoritmene bruker multiplikasjon, slik at De blir enda raskere når karatsubamultiplikasjon brukes. De to andre algoritmene er sakte; de bruker bare tillegg og ingen multiplikasjon.
Kildekode
Implementeringer er tilgjengelige på flere språk:
-
Java: FastFibonacci.java (alle 3 algoritmer, timing benchmark, kjørbart hovedprogram)
-
Python: fastfibonacci.py (rask dobling funksjon bare)
-
Haskell: fastfibonacci.hs (kun hurtig doblingsfunksjon)
-
C#: FastFibonacci. cs (kun rask dobling, kjørbart hovedprogram)
(krever. NET Framework 4.0 eller høyere; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
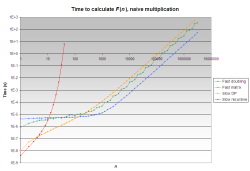
All algorithms, naive multiplication
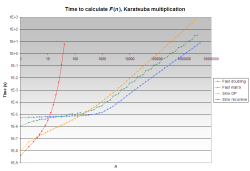
All algorithms, Karatsuba multiplication
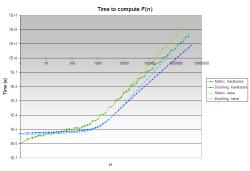
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive | |
|---|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 | |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 | |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 | |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 | |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 | |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 | |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 | |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 | |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 | |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 | |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 | |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 | |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 | |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 | |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | ||
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | ||
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | ||
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | ||
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | ||
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | ||
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | ||
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | ||
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | ||
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | ||
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | ||
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | ||
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | ||
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | ||
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | ||
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | ||
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | ||
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | ||
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | ||
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | ||
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | ||
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | ||
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | ||
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | ||
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | ||
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | ||
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | ||
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | ||
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | ||
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | ||
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | ||
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | ||
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | ||
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | ||
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | ||
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | ||
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | ||
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | ||
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | ||
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | ||
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | ||
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | ||
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | ||
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | ||
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | ||
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | ||
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | ||
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | ||
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | 7 654 000 000 |
alle tider er gitt i nanosekunder (ns), gitt til 4 signifikante tall. Alle testene ovenfor ble utført På Intel Core 2 Quad Q6600 (2.40 GHz) ved hjelp Av En enkelt tråd, Windows XP SP 3, Java 1.6.0_22.
Proofs
matrix exponentiation
vi vil bruke svak induksjon for å bevise denne identiteten.
Base case
for \(n = 1\), klart \ (\venstre^1 = \ venstre \).
Induksjonstrinn
Anta for \(n ≥ 1\) at \ (\venstre^n = \ venstre \). Deretter:
\(\venstre^{n+1} \ \ = \ venstre^n \ venstre \ \ = \ venstre \ \ = \ venstre \ \ = \ venstre \ \ \ venstre.\)
Rask dobling
vi antar at matriseeksponeringsmetoden er riktig for alle \(n ≥ 1\).
\(\venstre \ \ = \ venstre^{2n} \ \ = \ venstre (\venstre^n \ høyre)^2 \ \ = \ venstre^2 \ \ = \ venstre.\)
derfor, ved å likestille cellene i matrisen:
\(\begin{align}F(2n+1) &= F(n+1)^2 + F (n)^2. \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)