Blog
w poprzednim wpisie na blogu omówiliśmy, w jaki sposób supermarkety wykorzystują dane, aby lepiej zrozumieć potrzeby konsumentów i ostatecznie zwiększyć ich ogólne wydatki. Jedną z kluczowych technik stosowanych przez dużych sprzedawców detalicznych jest analiza koszyka rynkowego (ang. Market Basket Analysis, MBA), która odkrywa skojarzenia między produktami poprzez poszukiwanie kombinacji produktów, które często występują w transakcjach. Innymi słowy, pozwala supermarketom zidentyfikować relacje między produktami, które ludzie kupują. Na przykład klienci, którzy kupują ołówek i papier, prawdopodobnie kupują gumę lub linijkę.
„Analiza koszyka rynkowego pozwala detalistom zidentyfikować relacje między produktami, które kupują ludzie.”
sprzedawcy detaliczni mogą korzystać z wiedzy uzyskanej z MBA na wiele sposobów, w tym:
- grupowanie produktów, które występują wspólnie w projektowaniu układu sklepu, aby zwiększyć szansę na cross-selling;
- prowadzenie silników rekomendacji online („klienci, którzy kupili ten produkt, przeglądali również ten produkt”); i
- kierowanie kampanii marketingowych poprzez wysyłanie kuponów promocyjnych do klientów na produkty związane z ostatnio zakupionymi przedmiotami.
biorąc pod uwagę, jak popularny i wartościowy jest MBA, pomyśleliśmy, że przygotujemy następujący przewodnik krok po kroku opisujący, jak to działa i jak możesz podjąć się własnej analizy koszyka rynkowego.
jak działa Analiza koszyka rynkowego?
aby przeprowadzić MBA musisz najpierw zestaw danych transakcji. Każda transakcja reprezentuje grupę przedmiotów lub produktów, które zostały zakupione razem i często nazywane „zestawem przedmiotów”. Na przykład jednym zestawem elementów może być: {ołówek, papier, zszywki, guma}, w którym to przypadku wszystkie te elementy zostały zakupione w ramach jednej transakcji.
w MBA, transakcje są analizowane w celu określenia zasad Stowarzyszenia. Na przykład jedną z reguł może być: {pencil, paper} = > {rubber}. Oznacza to, że jeśli Klient ma transakcję, która zawiera ołówek i papier, prawdopodobnie będzie zainteresowany również zakupem gumy.
przed podjęciem działania zgodnie z regułą sprzedawca detaliczny musi wiedzieć, czy istnieją wystarczające dowody sugerujące, że doprowadzi to do korzystnego wyniku. Dlatego mierzymy siłę reguły, obliczając następujące trzy metryki (zauważ, że inne metryki są dostępne, ale są to trzy najczęściej używane):
Wsparcie: procent transakcji, które zawierają wszystkie elementy w zestawie elementów (np. ołówek, papier i guma). Im wyższe Wsparcie, tym częściej występuje zestaw elementów. Preferowane są zasady o wysokim poparciu, ponieważ prawdopodobnie będą miały zastosowanie do dużej liczby przyszłych transakcji.
pewność: prawdopodobieństwo, że transakcja zawierająca elementy po lewej stronie reguły (w naszym przykładzie ołówek i papier) zawiera również element po prawej stronie (gumka). Im większe zaufanie, tym większe prawdopodobieństwo, że przedmiot po prawej stronie zostanie zakupiony lub, innymi słowy, większa stopa zwrotu można oczekiwać dla danej reguły.
Lift: prawdopodobieństwo wszystkich elementów w regule występujących razem (inaczej zwanych wsparciem) podzielone przez iloczyn prawdopodobieństwa elementów po lewej i prawej stronie występujących tak, jakby nie było między nimi związku. Na przykład, jeśli ołówek, papier i guma wystąpiły razem w 2,5% wszystkich transakcji, ołówek i papier w 10% transakcji i guma w 8% transakcji, to Winda byłaby: 0.025/(0.1*0.08) = 3.125. Podniesienie o więcej niż 1 sugeruje, że obecność ołówka i papieru zwiększa prawdopodobieństwo, że guma pojawi się również w transakcji. Ogólnie rzecz biorąc, lift podsumowuje siłę powiązania między produktami po lewej i prawej stronie reguły; im większy podnośnik, tym większy związek między tymi dwoma produktami.
aby przeprowadzić analizę koszyka rynkowego i zidentyfikować potencjalne reguły, powszechnie stosuje się algorytm eksploracji danych zwany „algorytmem Apriori”, który działa w dwóch etapach:
- systematycznie identyfikuje zestawy elementów, które występują często w zbiorze danych z obsługą większą niż wstępnie określony próg.
- Oblicz ufność wszystkich możliwych reguł biorąc pod uwagę częste zestawy elementów i Zachowaj tylko te, które mają ufność większą niż wstępnie określony próg.
progi, przy których należy ustawić wsparcie i zaufanie, są określone przez użytkownika i prawdopodobnie różnią się między zestawami danych transakcji. R ma wartości domyślne, ale zalecamy eksperymentowanie z nimi, aby zobaczyć, jak wpływają one na liczbę zwracanych reguł (więcej na ten temat poniżej). Wreszcie, chociaż algorytm Apriori nie używa lift do ustanawiania reguł, zobaczysz poniżej, że używamy lift podczas odkrywania reguł, które algorytm zwraca.
przeprowadzanie analizy koszyka rynkowego w R
aby zademonstrować, jak przeprowadzić MBA, zdecydowaliśmy się użyć r, a w szczególności pakietu arules. Dla tych, którzy są zainteresowani, zamieściliśmy kod R, którego użyliśmy na końcu tego bloga.
tutaj podążamy za tym samym przykładem używanym w winiecie arulesViz i używamy zestawu danych sprzedaży spożywczej, który zawiera 9835 pojedynczych transakcji z 169 pozycjami. Pierwszą rzeczą, jaką robimy, jest przyjrzenie się pozycjom w transakcjach, a w szczególności wykreślić względną częstotliwość 25 najczęstszych pozycji na rysunku 1. Jest to równoznaczne z obsługą tych pozycji, gdzie każdy zestaw elementów zawiera tylko jeden element. Ten wykres ilustruje Artykuły spożywcze, które są często kupowane w tym sklepie, i warto zauważyć, że obsługa nawet najczęstszych przedmiotów jest stosunkowo niska (na przykład najczęstszy przedmiot występuje tylko w około 2,5% transakcji). Wykorzystujemy te spostrzeżenia, aby poinformować o minimalnym progu podczas uruchamiania algorytmu Apriori; na przykład, wiemy, że aby algorytm zwrócił rozsądną liczbę reguł, musimy ustawić próg wsparcia na znacznie poniżej 0.025.
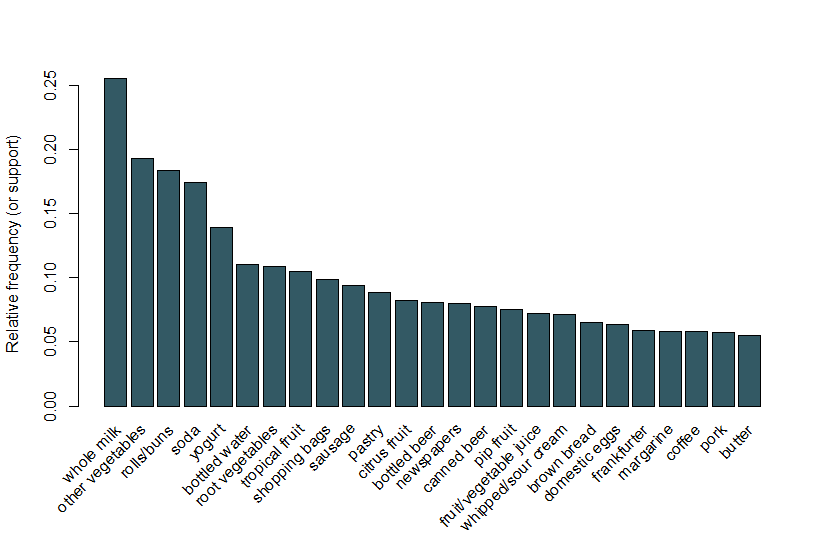
Rysunek 1 Wykres słupkowy wsparcia 25 najczęściej kupowanych przedmiotów.
ustawiając próg wsparcia 0.001 i pewność 0.5, możemy uruchomić algorytm Apriori i uzyskać zestaw 5668 wyników. Te wartości progowe są wybierane w taki sposób, że liczba zwracanych reguł jest wysoka, ale liczba ta zmniejszyłaby się, jeśli zwiększylibyśmy którykolwiek z nich. Zalecamy eksperymentowanie z tymi progami, aby uzyskać najbardziej odpowiednie wartości. Chociaż istnieje zbyt wiele reguł, aby móc spojrzeć na nie indywidualnie,możemy spojrzeć na pięć reguł z największą windą:
| reguła | wsparcie | pewność | Winda |
| {instant food products, soda}=>{hamburger Meat} | 0.001 | 0.632 | 19.00 |
| {soda, popcorn}=>{słone przekąski} | 0.001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. Na przykład pierwsza zasada może reprezentować rodzaj przedmiotów zakupionych na grilla, druga na noc filmową, a trzecia do pieczenia.
zamiast używać progów w celu zmniejszenia reguł do mniejszego zbioru, Zwykle zwracany jest większy zbiór reguł, dzięki czemu istnieje większa szansa na wygenerowanie odpowiednich reguł. Alternatywnie, możemy użyć technik wizualizacji, aby sprawdzić zbiór zwróconych reguł i zidentyfikować te, które mogą być użyteczne.
korzystając z pakietu arulesViz, rysujemy reguły przez confidence, support I lift na rysunku 2. Wykres ten ilustruje zależność między różnymi metrykami. Wykazano, że optymalnymi zasadami są te, które leżą na tzw. „granicy wsparcia i zaufania”. Zasadniczo są to zasady, które leżą na prawej granicy fabuły, gdzie albo wsparcie, zaufanie lub oba są zmaksymalizowane. Funkcja wykresu w pakiecie arulesViz ma przydatną funkcję interaktywną, która pozwala wybrać poszczególne reguły (klikając powiązany punkt danych), co oznacza, że reguły na granicy można łatwo zidentyfikować.
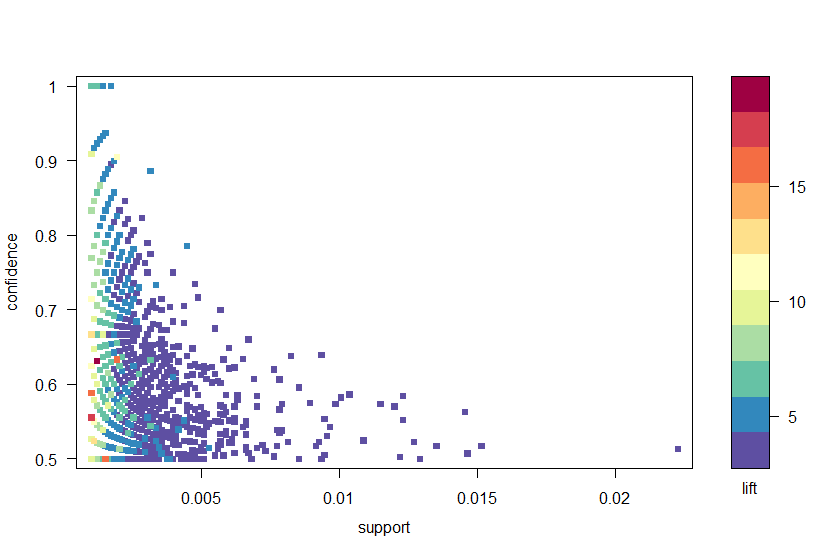
Rysunek 2: wykres punktowy wskaźników ufności, wsparcia i podnoszenia.
istnieje wiele innych wykresów dostępnych do wizualizacji reguł, ale jedną inną figurą, którą zalecamy zbadać, jest wizualizacja oparta na wykresach (patrz rysunek 3) dziesięciu najlepszych reguł pod względem lift (możesz uwzględnić więcej niż dziesięć, ale tego typu wykresy mogą łatwo się zaśmiecić). Na tym wykresie elementy zgrupowane wokół okręgu reprezentują zestaw elementów, a strzałki wskazują relację w regułach. Na przykład jedną z reguł jest to, że zakup cukru wiąże się z zakupem mąki i proszku do pieczenia. Wielkość okręgu reprezentuje poziom pewności związany z regułą, a kolor poziom podniesienia (im większe koło i im ciemniejsza szarość tym lepiej).
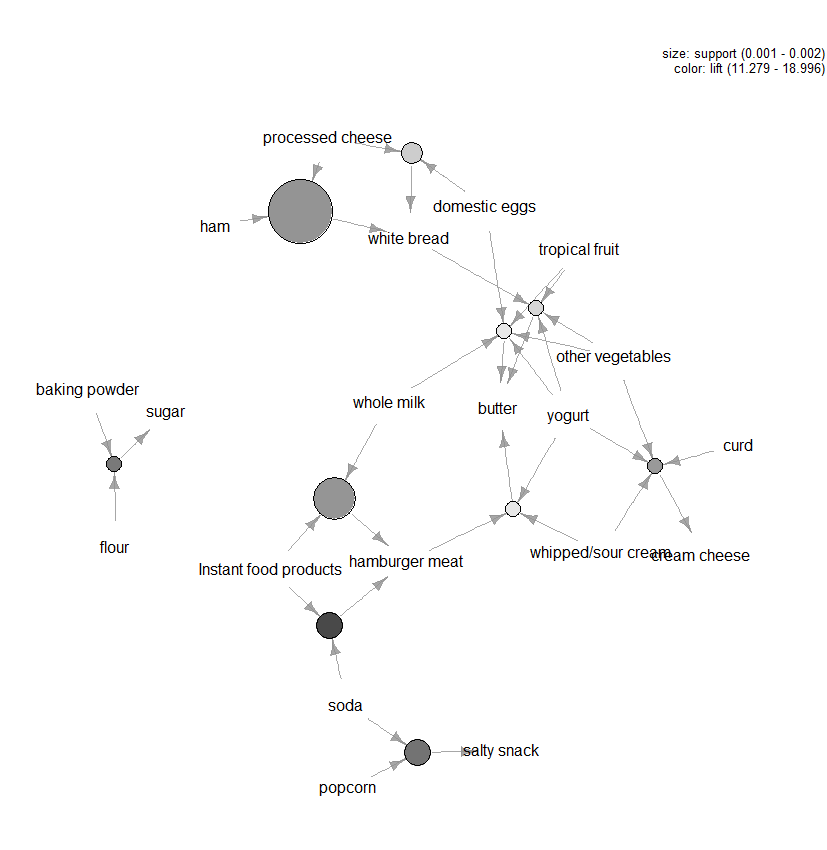
Rysunek 3: wizualizacja dziesięciu najważniejszych reguł pod względem lift.
Analiza koszyka rynkowego jest przydatnym narzędziem dla sprzedawców detalicznych, którzy chcą lepiej zrozumieć relacje między produktami, które kupują ludzie. Istnieje wiele narzędzi, które mogą być stosowane podczas przeprowadzania MBA i najtrudniejszych aspektów do analizy są ustawienie progów zaufania i wsparcia w algorytmie Apriori i określenie, które zasady są warte realizacji. Zazwyczaj odbywa się to poprzez pomiar reguł pod względem metryk, które podsumowują, jak interesujące są, przy użyciu technik wizualizacji, a także bardziej formalnych statystyk wielowymiarowych. Ostatecznie kluczem do MBA jest wydobycie wartości z danych transakcyjnych poprzez budowanie zrozumienia potrzeb konsumentów. Tego typu informacje są nieocenione, jeśli jesteś zainteresowany działaniami marketingowymi, takimi jak cross-selling lub kampanie targetowane.
Jeśli chcesz dowiedzieć się więcej o tym, jak analizować dane transakcji, skontaktuj się z nami, a my chętnie Ci pomożemy.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.