gdzie pA i PB są odpowiednio częstotliwością alleli a i B w dwóch oddzielnych loci (X, Y) mierzone dla osób N, PAB jest częstością haplotypu z allelami a i b w badanej populacji, X i y są średnią częstością genotypu odpowiednio dla pierwszego i drugiego locus, XI jest genotypem osobnika i w pierwszym Locus, a yi jest genotypem osobnika i w drugim locus. Równanie (2) koreluje liczbę alleli genotypowych zamiast częstotliwości haplotypu i nie ma wpływu na podwójne heterozygoty (takie podejście daje takie same szacunki jak opcja — r2 w PLINK).

SNeP szacuje historyczną efektywną wielkość populacji w oparciu o zależność między r2, Ne i c (Współczynnik rekombinacji), (równanie 3—Sved, 1971)i umożliwiając użytkownikom uwzględnienie korekt wielkości próby i niepewności fazy gametycznej (równanie 4—Weir and Hill, 1980):

gdzie n to liczba pobranych osobników, β = 2, gdy faza gametyczna jest znana i β = 1, jeśli zamiast tego Faza nie jest znana.

kilka przybliżeń jest używanych do wnioskowania o szybkości rekombinacji, używając fizycznej odległości (δ) między dwoma loci jako odniesienia i tłumacząc ją na odległość połączenia (d), która jest zwykle opisywana jako Mb(δ) ≈ cM(d). Dla małych wartości d drugie przybliżenie jest ważne, ale dla większych wartości D prawdopodobieństwo wielokrotnych zdarzeń rekombinacji i interferencji wzrasta, ponadto zależność między odległością mapy a szybkością rekombinacji nie jest liniowa, ponieważ maksymalna możliwa szybkość rekombinacji wynosi 0,5. Tak więc, o ile nie zastosowano bardzo krótkiego δ, przybliżenie d ≈ c nie jest idealne (Corbin et al., 2012). Dlatego zaimplementowaliśmy funkcje mapowania, aby przetłumaczyć szacunkowe d NA c, po Haldane (1919), Kosambi (1943), Sved (1971) oraz Sved i Feldman (1973). Początkowo SNeP wnioskuje d dla każdej pary SNP jako wprost proporcjonalną do δ zgodnie z d = kδ, gdzie k jest wartością szybkości rekombinacji zdefiniowaną przez użytkownika (domyślna wartość to 10-8 jak w Mb = cM). Wnioskowana wartość δ może być następnie poddana jednej z dostępnych funkcji mapowania, jeśli jest to wymagane przez użytkownika.

rozwiązanie równania (3) dla Ne i włączenie wszystkich opisanych korekt, pozwala na przewidywanie Ne z danych LD za pomocą (Corbin et al., 2012):

gdzie Nt jest efektywną wielkością populacji t pokolenia temu obliczoną jako T = (2F(ct))-1 (Hayes et al., 2003), ct jest szybkością rekombinacji zdefiniowaną dla określonej fizycznej odległości między markerami i opcjonalnie dostosowaną za pomocą funkcji mapowania wymienionych powyżej, r2adj jest wartością LD dostosowaną do wielkości próbki, a α:= {1, 2, 2.2} jest korekcją występowania mutacji (Ohta i Kimura, 1971). W związku z tym, LD na większych odległościach rekombinacji ma charakter informacyjny w ostatnim Ne, podczas gdy krótsze odległości dostarczają informacji o bardziej odległych czasach w przeszłości. System binning jest zaimplementowany w celu uzyskania uśrednionych wartości r2, które odzwierciedlają LD dla określonych odległości między locus. Zaimplementowany system binning wykorzystuje następującą formułę do definiowania minimalnych i maksymalnych wartości dla każdego bin:

gdzie Bi (ℕ1) jest i-tym pojemnikiem z całkowitej liczby pojemników (totBins), minD I maxD są odpowiednio minimum i maksimum odległość między SNPs i X jest dodatnią liczbą rzeczywistą (ℝ0) gdy x jest równe 1, rozkład odległości między pojemnikami jest liniowy i każdy pojemnik ma ten sam zakres odległości. Dla większych wartości x rozkład odległości zmienia się, umożliwiając większy zakres na ostatnich pojemnikach i mniejszy zakres na pierwszych pojemnikach. Zmiana tego parametru pozwala użytkownikowi mieć wystarczającą liczbę porównań par, aby przyczynić się do ostatecznego oszacowania Ne dla każdego pojemnika.

Przykładowa aplikacja

testowaliśmy SNeP z dwoma opublikowanymi zestawami danych, które były wcześniej używane do opisywania trendów w Ne w czasie za pomocą LD, Bos indicus i Ovis aries . Szacunki r2 dla zbiorów danych dla bydła zostały uzyskane przez autorów przy użyciu GenABLE (Aulchenko et al., 2007) stosując minimalną częstotliwość alleli (MAF) < 0.01 i dostosowując szybkość rekombinacji za pomocą funkcji mapowania Haldane ’ a (Haldane, 1919). Szacunki R2 dotyczące danych dotyczących owiec zostały obliczone przez autorów za pomocą PLINK-1.07 (Purcell et al., 2007), z MAF < 0.05 i bez dalszych poprawek. Dla obu autosomalnych zestawów danych szacunki r2, skorygowane o wielkość próbki za pomocą równania (4) z β = 2. Do tych analiz porównawczych linia poleceń SNeP zawierała te same parametry, które zostały użyte do opublikowanych danych, oprócz szacunków r2, obliczonych na podstawie liczby genotypów i zastosowania nowej strategii binningu SNeP.

wyniki

SNeP to wielowątkowa aplikacja opracowana w C++ i pliki binarne dla najpopularniejszych systemów operacyjnych (Windows, OSX i Linux) można pobrać zhttps://sourceforge.net/projects/snepnetrends/. Do binariów dołączony jest podręcznik opisujący krok po kroku wykorzystanie SNeP do wnioskowania trendów w Ne, jak opisano tutaj. SNeP tworzy plik wyjściowy z kolumnami rozdzielonymi tabulatorami pokazującymi dla każdego pojemnika, który został użyty do oszacowania Ne: liczbę generacji w przeszłości, której odpowiada Pojemnik (np., 50 generations ago), odpowiednie oszacowanie Ne, średnia odległość między każdą parą SNP w pojemniku, średnia r2 i odchylenie standardowe r2 w pojemniku oraz liczba SNP użytych do obliczenia r2 w pojemniku. Plik ten można łatwo zaimportować w programie Microsoft Excel, R lub innym oprogramowaniu w celu wykreślenia wyników. Wykresy pokazane tutaj (ryciny 1, 3) odpowiadają kolumnom sprzed pokoleń i Ne z pliku wyjściowego. Kolumna z odchyleniem standardowym r2 jest przeznaczona dla użytkowników w celu sprawdzenia wariancji w estymacie Ne w każdym pojemniku, szczególnie dla tych pojemników odzwierciedlających starsze szacunki czasowe i które są mniej wiarygodne, ponieważ liczba SNP używanych do oszacowania r2 staje się mniejsza.

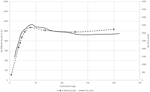
Rysunek 1. Porównanie Ne trendów sześciu Szwajcarskich ras owiec według Burren et al. (2014) (przerywane linie) i ta praca (solid lines).

format wymagany dla plików wejściowych to standardowy format PLINK (ped i pliki map) (Purcell et al., 2007). SNeP pozwala użytkownikom obliczyć LD na podstawie danych opisanych powyżej lub użyć niestandardowej wstępnie obliczonej macierzy LD do oszacowania Ne za pomocą równania (5).

interfejs oprogramowania pozwala użytkownikowi kontrolować wszystkie parametry analizy, np. zakres odległości między SNP w bp, a zestawem chromosomów wykorzystywanych w analizie (np. 20-23). Dodatkowo SNeP zawiera opcję wyboru progu MAF (Domyślnie 0.05), ponieważ wykazano, że rozliczanie MAF daje bezstronne szacunki r2 niezależnie od wielkości próby (Sved et al., 2008). Wielowątkowa Architektura SNeP pozwala na szybkie obliczanie dużych zbiorów danych (testowaliśmy do ~100k SNPs dla pojedynczego chromosomu), na przykład opisane tutaj dane BOS analizowano z jednym procesorem na 2’43”, użycie dwóch procesorów skróciło czas analizy do 1’43”, cztery procesory skróciły czas analizy do 1’05”.

przykład Zebu

dla analizy zebu kształty krzywych Ne uzyskane za pomocą SNeP i ich opublikowane trendy danych wykazały tę samą trajektorię z płynnym spadkiem aż do około 150 pokoleń temu, a następnie ekspansję ze szczytem około 40 pokoleń temu i kończąc się stromym spadkiem w ostatnich pokoleniach (ryc. 1). Jednak podczas gdy trendy w obu krzywych były takie same, oba podejścia doprowadziły do różnych szacunków Ne, przy czym wartości SNeP były około trzykrotnie większe niż w oryginalnym artykule. Podczas gdy próbowaliśmy wykorzystać parametry autorów w naszych analizach, pewne różnice były nieuniknione, tj. oryginalna publikacja danych dotyczących bydła oszacowała r2 z innym podejściem niż zaimplementowane w SNeP. Analizy z użyciem SNeP opierały się na genotypach, podczas gdy pierwotna analiza opierała się na wnioskowanych dwóch haplotypach locus, co skutkowało opublikowanymi danymi pokazującymi oczekiwany r2 na poziomie 0,32 w minimalnej odległości, podczas gdy nasze szacunki wynosiły 0,23. Podobnie Mbole-Kariuki et al. (2014) uzyskał poziom tła r2 = 0,013 około 2 Mb, podczas gdy nasze szacunki w tej samej odległości wynosiły 0.0035 (dane nie pokazane). W związku z tym, jak nasze szacunki LD były konsekwentnie mniejsze niż Mbole-Kariuki et al. (2014) oczekuje się, że nasze szacunki ne powinny być większe. Podczas gdy ta obserwacja podkreśla znaczenie starannego wyboru parametrów i ich progów, ważne jest, aby podkreślić, że chociaż absolutna wielkość wartości Ne jest inna, trendy są prawie identyczne.

Swiss Sheep Example

sześć Szwajcarskich ras owiec analizowanych za pomocą SNeP dało porównywalne wyniki z tymi z oryginalnego artykułu (rycina 2), z najczęściej nakładającymi się krzywymi trendu Ne (rycina 3). Jednak ogólny trend w Ne wykazał spadek w kierunku teraźniejszości. SNeP wytworzył nieco większe wartości Ne dla bardziej odległej przeszłości (700-800 pokoleń). Wynika to z innego systemu binningu stosowanego w SNeP, który pozwala użytkownikowi uzyskać bardziej równomierny rozkład porównań par w każdym pojemniku (np., liczba porównań par SNP w każdym pojemniku jest porównywalna). W okresie wykraczającym poza 400 pokoleń temu, Burren et al. (2014) wykorzystał tylko trzy pojemniki w swojej analizie (skupione na 400, 667 i 2000 pokoleń temu), podczas gdy w tym samym czasie SNeP użył 5 pojemników z liczbą porównań par zależnych od zakresu zdefiniowanego wzorem 6A,b. W związku z tym podejście Burrena i współpracowników kończy się większą gęstością danych opisujących najnowsze pokolenia niż opisujących najstarsze pokolenia. Dlatego też stosowanie mniejszej liczby pojemników ma tendencję do zwiększania obecności mniejszych wartości Ne w każdym pojemniku, w konsekwencji obniżając średnią wartość Ne dla każdego pojemnika. Wartości Ne dla niedawnej przeszłości, w porównaniu z 29. generacją w przeszłości, dały bardzo podobne wyniki. Największą różnicę (50) uzyskano dla rasy SBS.

Rysunek 2. Porównanie ostatnich wartości ne obliczonych w 29 generacji w tej pracy i Burren et al. (2014) dla sześciu Szwajcarskich ras owiec.

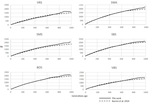
Rysunek 3. Porównanie trendów Ne dla ostatnich 250 generacji w danych SHZ uzyskanych przez Mbole-Kariuki et al. (2014) (linia przerywana) i przy użyciu SNeP (linia ciągła).

dyskusja

Analiza Ne przy użyciu danych LD została po raz pierwszy zademonstrowana 40 lat temu i była stosowana, rozwijana i ulepszana od tego czasu (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Tradycyjnie mała liczba analizowanych SNP nie jest już ograniczeniem, ponieważ chipy SNP zawierają bardzo dużą liczbę SNP, dostępnych w krótkim czasie i za rozsądną cenę. To zwiększyło wykorzystanie metody, która została zastosowana do ludzi (Tenesa et al., 2007; McEvoy et al., 2011), a także do kilku udomowionych gatunków (England et al., 2006; Uimari and Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Wraz z tymi ulepszeniami widoczne stały się ograniczenia metodologiczne, które zostały tutaj omówione, przy czym większość wysiłków wskazuje na poprawne oszacowanie niedawnych Ne. Jednak wartość ilościowa oszacowania jest w dużym stopniu zależna od wielkości próby, rodzaju estymacji LD i procesu binningu (Waples and Do, 2008; Corbin et al., 2012), podczas gdy jego wzór jakościowy zależy bardziej od informacji genetycznej niż od manipulacji danymi.

do tej pory metoda ta była stosowana przy użyciu różnych programów, nie istnieje standardowe podejście do binowania wyników i każde badanie zastosowało mniej lub bardziej arbitralne podejście, np. binowanie dla klas generowania w przeszłości (Corbin et al., 2012), binning dla klas odległości ze stałym zakresem dla każdego bin (Kijas et al., 2012) lub binning na klasy odległości w sposób liniowy, ale z większymi pojemnikami na nowsze punkty czasowe (Burren et al., 2014). Według naszej wiedzy jedynym dostępnym oprogramowaniem, które szacuje Ne przez LD jest NeEstimator (do et al., 2014), ulepszona wersja dawnego Ldne (Waples and Do, 2008) umożliwiająca analizę dużego zbioru danych (jako 50k SNPChip). Co ważne, podczas gdy SNeP koncentruje się na szacowaniu historycznych trendów Ne, celem Neestimatora jest opracowanie współczesnych bezstronnych szacunków Ne, te ostatnie należy zatem uznać za narzędzie uzupełniające podczas badania demografii za pomocą LD.

użyliśmy SNeP do analizy dwóch zbiorów danych, w których metoda była wcześniej zastosowana. Wyniki uzyskane dla danych dotyczących owiec były zarówno pod względem ilościowym, jak i jakościowym porównywalne z wynikami uzyskanymi przez Burren et al. (2014), podczas gdy dla danych Zebu uzyskaliśmy estymację trendu Ne, która ściśle pasowała do Mbole-Kariuki et al. (2014) chociaż nasze szacunki punktowe Ne były większe niż te opisane dla danych (Mbole-Kariuki et al., 2014). Rozbieżność między tymi dwoma wynikami odzwierciedla to, że Burren i współpracownicy wyprodukowali swoje szacunki r2 przy użyciu PLINK (standardowe oprogramowanie do manipulacji danymi SNP na dużą skalę), które wykorzystuje to samo podejście stosowane do szacowania R2 przez SNeP, podczas gdy Mbole-Kariuki et al. następnie Hao et al. (2007) dla oszacowania r2. Zastosowanie różnych szacunków dla LD ma kluczowe znaczenie dla ilościowego aspektu krzywej Ne, gdzie ze względu na korelację hiperboliczną między Ne I r2, spadek r2 na jego zakresie bliżej 0 może prowadzić do bardzo dużej zmiany szacunków Ne, podczas gdy różnice w szacunkach są mniej znaczące, gdy wartość r2 jest wysoka, tj. bliżej 1. Dlatego, chociaż w jednym z zestawów danych wartości Ne były zasadniczo różne, w obu przypadkach krzywe Ne pokrywały się z tymi pierwotnie opublikowanymi.

jak już sugerują inni autorzy, wiarygodność szacunków ilościowych uzyskanych tą metodą należy zachować ostrożność, szczególnie w przypadku wartości Ne związanych z najnowszymi i najstarszymi pokoleniami (Corbin et al., 2012) ponieważ w przypadku ostatnich pokoleń zaangażowane są duże wartości c, nie pasujące do teoretycznych implikacji, które Hayes zaproponował, aby oszacować zmienną Ne w czasie (Hayes et al., 2003). Szacunki dla najstarszych pokoleń mogą być również niewiarygodne, ponieważ teoria koalescencyjna pokazuje, że żaden SNP nie może być wiarygodnie pobrany po 4 kolejnych pokoleniach w przeszłości(Corbin et al., 2012). Co więcej, szacunki Ne, a zwłaszcza te związane z pokoleniami w przeszłości, są silnie uzależnione od czynników manipulacji danymi, takich jak wybór wartości MAF i Alfa. Dodatkowo zastosowana strategia binningu może zakłócać ogólną precyzję metody, na przykład gdy do zapełnienia każdego pojemnika używana jest niewystarczająca liczba porównań par.

jednym z zastosowań metody jest porównanie demografii ras. W tym przypadku kształt krzywych Ne byłby optymalnym narzędziem do różnicowania różnych historii demograficznych, bardziej niż ich wartości liczbowych, poprzez wykorzystanie ich jako potencjalnego demograficznego odcisku palca dla tej rasy lub gatunku, jednak biorąc pod uwagę, że mutacja, migracja i selekcja mogą wpływać na estymację Ne poprzez LD (Waples and Do, 2010). Dodatkowo, staranne rozważenie danych analizowanych za pomocą SNeP (i innego oprogramowania do szacowania Ne) jest bardzo ważne, ponieważ obecność czynników zakłócających, takich jak domieszka, może spowodować stronnicze szacunki Ne (Orozco-terWengel and Bruford, 2014).

celem SNeP jest zatem zapewnienie szybkiego i niezawodnego narzędzia do stosowania metod LD do szacowania Ne przy użyciu danych genotypowych o wysokiej przepustowości w bardziej spójny sposób. Pozwala na dwa różne podejścia do szacowania r2 plus możliwość korzystania z szacowania R2 z zewnętrznego oprogramowania. Zastosowanie SNeP nie przekracza granic metody i teorii, która za nią stoi, ale pozwala użytkownikowi zastosować teorię przy użyciu wszystkich proponowanych do tej pory poprawek.

author Contributions

MB, MT i POtW przetestowały oprogramowanie i przeprowadziły analizy. MT, POtW i MWB poprawiły rękopis. Wszyscy autorzy zatwierdzili ostateczny manuskrypt.

Oświadczenie o konflikcie interesów

autorzy oświadczają, że badanie zostało przeprowadzone przy braku jakichkolwiek relacji handlowych lub finansowych, które mogłyby być interpretowane jako potencjalny konflikt interesów.

podziękowania

dziękujemy Christine Flury za dostarczenie danych o owcach i przydatną dyskusję. Dziękujemy również dwóm recenzentom za przydatne sugestie dotyczące ulepszenia tego artykułu. MB był obsługiwany przez Program Master and Back (Regione Sardegna).