filtry Kalmana

algorytm używany do scalania danych nazywa się filtrem Kalmana.

Filtr Kalmana jest jednym z najpopularniejszych algorytmów fuzji danych. Wynaleziony w 1960 roku przez Rudolpha Kalmana, jest obecnie używany w naszych telefonach lub satelitach do nawigacji i śledzenia. Najbardziej znane użycie filtra było podczas misji Apollo 11, Aby wysłać i sprowadzić załogę z powrotem na Księżyc.

kiedy stosować filtr Kalmana ?

Filtr Kalmana może być użyty do fuzji danych w celu oszacowania stanu dynamicznego systemu (ewoluującego z czasem) w teraźniejszości (filtrowanie), przeszłości (wygładzanie) lub przyszłości (przewidywanie). Czujniki wbudowane w autonomiczne pojazdy emitują pomiary, które czasami są niekompletne i hałaśliwe. Niedokładność czujników (szum) jest bardzo ważnym problemem i może być obsługiwana przez filtry Kalmana.

Filtr Kalmana jest używany do oszacowania stanu układu, oznaczonego x. wektor ten składa się z pozycji p i prędkości v.

przy każdym oszacowaniu kojarzymy miarę niepewności p.

wykonując fuzję czujników, bierzemy pod uwagę różne dane dla tego samego obiektu. Radar może oszacować, że pieszy jest w odległości 10 metrów, podczas gdy Lidar szacuje go na 12 metrów. Zastosowanie filtrów Kalman pozwala mieć precyzyjny pomysł, aby zdecydować, ile metrów naprawdę jest pieszy, eliminując hałas dwóch czujników.

Filtr Kalmana może generować szacunki stanu obiektów wokół niego. Aby dokonać oszacowania, potrzebuje tylko bieżących obserwacji i poprzedniej prognozy. Historia pomiarów nie jest konieczna. To narzędzie jest zatem lekkie i poprawia się z czasem.

Jak to wygląda

stan i niepewność są reprezentowane przez Gaussa.

Gaussian jest funkcją ciągłą, pod którą pole wynosi 1. To pozwala nam reprezentować prawdopodobieństwa. Mamy Prawdopodobieństwo do rozkładu normalnego. Uni-modalność filtrów Kalmana oznacza, że za każdym razem mamy pojedynczy szczyt, aby oszacować stan systemu.

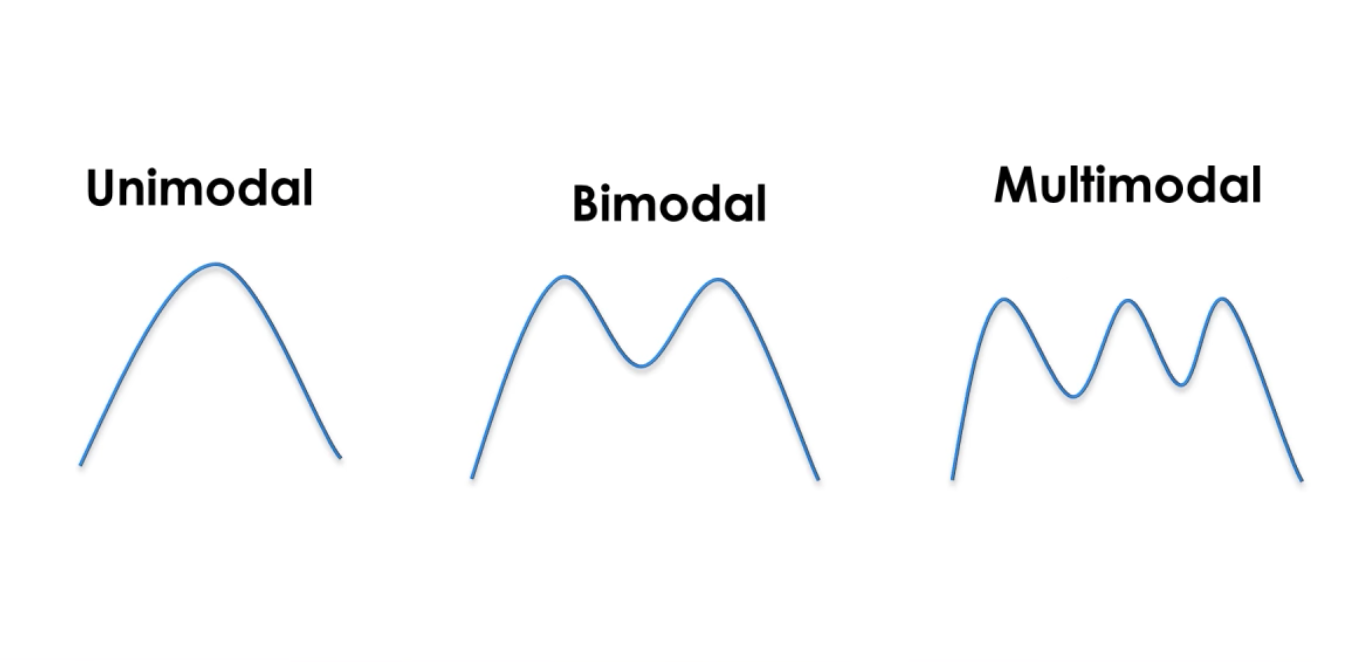
mamy średnią μ reprezentującą stan i wariancję σ2 reprezentującą niepewność. Im większa wariancja, tym większa niepewność.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Wykorzystujemy obserwacje naszych czujników, aby skorygować przewidywany stan i uzyskać dokładniejsze oszacowanie.

aby dokonać oszacowania, filtr Kalmana potrzebuje tylko bieżących obserwacji i poprzedniej prognozy. Historia pomiarów nie jest konieczna.

Matematyka

matematyka za filtrami Kalmana składa się z uzupełnień i mnożeń macierzy. Mamy dwa etapy: przewidywanie i aktualizacja.

Predykcja
nasza PREDYKCJA polega na oszacowaniu stanu x’ i niepewności P’ w czasie t z poprzednich stanów x I P w czasie T-1.

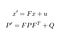
• f: macierz przejścia z t-1 Na t
• ν: dodano szum
• Q:
  

  

  

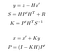
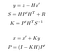
  • y: różnica między rzeczywistym pomiarem a prognozowaniem, tj. błąd.
  • s: szacowany błąd systemu
  • H: macierz przejścia między znacznikiem czujnika a naszym.
  • R: Matryca kowariancji związana z szumem czujnika (podana przez producenta czujnika).
  • K: Kalman gain. Współczynnik od 0 do 1 odzwierciedlający potrzebę skorygowania naszej prognozy.

  Faza aktualizacji umożliwia oszacowanie x I P bliżej rzeczywistości niż to, co dostarczają pomiary.

  Filtr Kalmana umożliwia przewidywanie w czasie rzeczywistym, bez wcześniejszego podawania danych. Używamy modelu matematycznego opartego na mnożeniu macierzy za każdym razem definiującego stan x (pozycja, prędkość) i niepewność P.

  Représentation Prior/Posterior

  ten diagram pokazuje, co dzieje się w filtrze Kalmana.

  

  • przewidywany stan przedstawia nasz pierwszy szacunek, naszą fazę przewidywania. Mówimy o przeorze.
  • Pomiar to pomiar z jednego z naszych czujników. Mamy lepszą niepewność, ale hałas czujników sprawia, że pomiar jest zawsze trudny do oszacowania. Mówimy o prawdopodobieństwie.
  • optymalne oszacowanie stanu to nasza Faza aktualizacji. Niepewność jest Tym razem najsłabsza, zgromadziliśmy informacje i pozwoliliśmy wygenerować wartość pewniejszą niż w przypadku samego naszego czujnika. Ta wartość jest naszym najlepszym przypuszczeniem. Mówimy o posterior.

  to, co filtr Kalmana implementuje, jest w rzeczywistości regułą Bayesa.

  

  w filtrze Kalmana zapętlamy prognozy z pomiarów. Nasze prognozy są zawsze bardziej precyzyjne, ponieważ utrzymujemy miarę niepewności i regularnie obliczamy błąd między naszą prognozą a rzeczywistością. Na podstawie macierzy mnożenia i wzorów prawdopodobieństwa jesteśmy w stanie oszacować prędkości i pozycje pojazdów wokół nas.

  „Rozszerzone/bezzapachowe” filtry i Nieliniowość

  pojawia się istotny problem. Nasze wzory matematyczne są zaimplementowane z funkcjami liniowymi typu y = ax + b.
  Filtr Kalmana zawsze działa z funkcjami liniowymi. Z drugiej strony, gdy używamy radaru, dane nie są liniowe.

  

  radar widzi świat z trzema miarami:

  te trzy wartości sprawiają, że nasz pomiar jest nieliniowy, biorąc pod uwagę włączenie kąta φ.

  naszym celem jest konwersja danych ρ, φ, ρ na dane kartezjańskie (px, py, vx, vy).

  Jeśli wprowadzamy dane nieliniowe do filtra Kalmana, nasz wynik nie jest już w postaci uni-modalnej Gaussa i nie możemy już oszacować pozycji i prędkości.

  

  używamy więc aproksymacji, dlatego pracujemy nad dwiema metodami:
  -rozszerzone filtry Kalmana wykorzystują serie jacobiana i Taylora do linearyzacji modelu.
  – bezzapachowe filtry Kalmana wykorzystują dokładniejsze przybliżenie do linearyzacji modelu.

  aby poradzić sobie z włączaniem nieliniowości przez Radar, istnieją techniki i pozwalają naszym filtrom oszacować położenie i prędkość obiektów, które chcemy śledzić.