Refraction, czyli zginanie światła, występuje, gdy światło przechodzi z jednego ośrodka do drugiego o innym współczynniku załamania światła. Refrakcja jest ważną cechą soczewek, pozwalającą im skupić wiązkę światła na jednym punkcie, a także jest odpowiedzialna za wiele znanych zjawisk, takich jak pozorne zniekształcenia obiektów częściowo zanurzonych w wodzie.

współczynnik załamania światła jest zdefiniowany jako względna prędkość, z jaką światło porusza się przez materiał w odniesieniu do jego prędkości w próżni. Zgodnie z konwencją współczynnik załamania próżni definiuje się jako mający wartość 1,0. Współczynnik załamania światła, n, innych materiałów przezroczystych jest zdefiniowany za pomocą równania:

gdzie c jest prędkością światła, a v jest prędkością światła w tym materiale. Ponieważ współczynnik załamania próżni jest zdefiniowany jako 1.0 i próżnia jest pozbawiona jakiegokolwiek materiału, współczynniki załamania wszystkich przezroczystych materiałów są zatem większe niż 1,0. Dla większości praktycznych celów współczynnik załamania światła przez powietrze (1.0003) może być użyty do obliczenia współczynników załamania nieznanych materiałów. Współczynniki załamania niektórych popularnych materiałów przedstawiono w tabeli 1 poniżej.

Materiał index air 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Na przykład, gdy światło przechodzi z mniej gęstego medium, takiego jak powietrze, do bardziej gęstego medium, takiego jak woda, prędkość, z jaką porusza się fala elektromagnetyczna, maleje. Alternatywnie, gdy światło przechodzi z bardziej gęstego medium do mniej gęstego medium, prędkość fali wzrasta.

kąt, pod jakim porusza się załamane światło, zależy jednak zarówno od kąta padania, jak i składu materiału, w który wchodzi. Normę można zdefiniować jako linię prostopadłą do granicy między dwiema substancjami. Światło przechodzi do granicy pod kątem do normy i jest załamywane zgodnie z Prawem Snella:

gdzie n oznacza współczynniki załamania materiału 1 i materiału 2, A q symbolizuje kąty światła poruszającego się przez te materiały w odniesieniu do normy. Istnieje kilka ważnych punktów, które można wyciągnąć z tego równania. Gdy n (1) jest większe niż n(2), kąt załamania jest zawsze mniejszy niż kąt padania. Alternatywnie, gdy n(2) jest większe niż n(1), kąt załamania jest zawsze większy niż kąt padania. Gdy dwa współczynniki załamania są równe(n(1) = n (2)), to światło jest przepuszczane bez załamania.

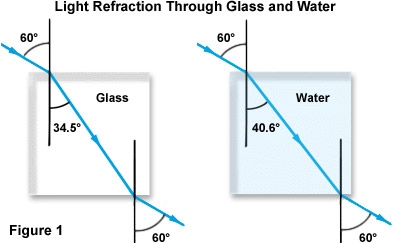
pojęcie współczynnika załamania światła zostało zilustrowane na rysunku 1 poniżej, skupiając się na przypadku światła przechodzącego z powietrza zarówno przez szkło, jak i wodę. Zauważ, że podczas gdy obie wiązki wchodzą do gęstszego materiału przez ten sam kąt padania w odniesieniu do normalnej (60 stopni), załamanie dla szkła jest prawie 6 stopni większe niż dla wody ze względu na wyższy współczynnik załamania szkła.

naukowcy odkryli, że współczynnik załamania różni się w zależności od częstotliwości promieniowania (lub długości fali) światła. Zjawisko to występuje w połączeniu ze wszystkimi przezroczystymi mediami i zostało nazwane dyspersją. Dlatego podczas pomiaru współczynnika załamania światła przezroczystej substancji należy określić konkretną długość fali stosowaną w pomiarze. Poniżej Tabela 2 szczegółowo opisuje dyspersję trzech niezależnych długości fal w różnych mediach.

Materiał niebieski (486,1 nm) żółty (589,3 nm) czerwony (656,3 nm) Crown Glass 1.524 1.517 1.515 szkło krzemienne 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Światło to jest nazywane widmem linii D i reprezentuje żółte światło wymienione w tabeli 2 powyżej. Podobnie, widma linii F i linii C odpowiadają niebieskiemu i czerwonemu światłu o określonych długościach fal emitowanych przez wodór. Widma Te są fundamentalne w obliczeniach dyspersji, które można ilościowo zdefiniować jako:

gdzie n jest współczynnikiem załamania materiału przy określonej długości fali oznaczonej przez D, F I C, które reprezentują linie widmowe sodu.i wodór jak omówiono powyżej. Zależność ta jest taka, że wraz ze wzrostem długości fali światła zmniejsza się współczynnik załamania światła. Jednak wiele czynników odgrywa rolę w dyspersji różnych materiałów, w tym ich skład elementarny i molekularny. Kilka nieorganicznych ciał stałych, takich jak chromiany, dichromiany, cyjanki, wanadany i kompleksy halogenkowe, ma niezwykle wysokie dyspersje. Jednak podstawniki organiczne mogą również przyczyniać się do wysokiej dyspersji.

	Interactive Java Tutorial
załamanie światła dowiedz się, jak długość fali i kąt padania światła wpływają na załamanie światła w różnych mediach o różnych współczynnikach załamania.

Refraction of light is particularly important in the construction and physics of lenses. Pamiętaj, że gdy wiązka światła wydostała się zarówno ze szkła, jak i z wody na fig.1, została ponownie załamana pod tym samym kątem, pod jakim weszła do materiału. Koncepcja ta jest niezbędna w funkcjonowaniu soczewek, choć kształt soczewki znacząco wpływa na uzyskany obraz. W soczewce wypukłej, jak pokazano poniżej na rysunku 2, fale świetlne odbite od obiektu, w tym przypadku żyrafy, są wygięte w kierunku optycznego środka soczewki i zbiegają się w punkcie ogniskowym.

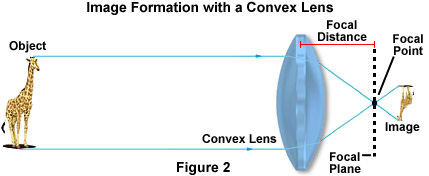
względne położenie obiektu względem przedniego punktu ogniskowej obiektywu określa sposób obrazowania obiektu. Jeśli obiekt jest ponad dwukrotnie dłuższy od ogniskowej, wydaje się mniejszy i odwrócony i musi być zobrazowany przez dodatkowy obiektyw w celu powiększenia rozmiaru. Jednak gdy obraz jest bliżej obiektywu niż punktu ogniskowego, obraz wydaje się pionowy i większy, co można łatwo zademonstrować za pomocą prostego szkła powiększającego.

	Interactive Java Tutorial
Powiększenie Obrazu dowiedz się, jak obraz żyrafy jest powiększany przez załamanie fal świetlnych przechodzące przez prostą cienką, dwuwypukłą soczewkę.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Prosta słomka do picia w szklance wypełnionej wodą, jak pokazano na fig. W tym przykładzie fale światła muszą najpierw przejść przez wodę, następnie przez granicę szkło / woda, a na koniec przez powietrze. Fale świetlne odbite od końców słomy są załamywane w większym stopniu niż te pochodzące ze środka słomy, dzięki czemu słoma wydaje się powiększona i lekko zniekształcona.

to samo zjawisko można wykorzystać do określenia współczynnika załamania światła cieczy za pomocą mikroskopu optycznego. Aby to zrobić, na wewnętrznej powierzchni szklanej należy umieścić płaską komórkę zdolną do trzymania cieczy ze znakiem (lub podziałką). Ponadto jedno z okularów mikroskopowych musi mieć włożoną siateczkę z podziałką na głównej płaszczyźnie obrazu w celu pomiaru szerokości linii znaku w płaskiej komórce. Przed dodaniem do komórki cieczy o nieznanym współczynniku załamania, mikroskop powinien skupić się na znaku na dnie komórki i odnotować pomiar położenia znaku na siatce. Następnie do komórki należy dodać niewielką ilość płynu, a mikroskop ponownie skierować na znak (przez ciecz) i wykonać nowy pomiar. Następnie mikroskop powinien być ostatecznie skupiony na powierzchni cieczy,a trzeci odczyt zapisany przez pomiar położenia znaku na siatce. Współczynnik załamania nieznanej cieczy można następnie obliczyć za pomocą następującego równania:

gdzie D(zmierzony) to zmierzona głębokość (od powierzchni cieczy do położenia znaku na pustej komórce) przy użyciu mikroskopu, a d(pozorny) to pomiar znaku z użyciem mikroskopu.i bez płynu.

krytyczny kąt odbicia jest kolejnym kluczowym pojęciem w badaniu załamania światła i jest zilustrowany poniżej na rysunku 4. Gdy światło przechodzi przez medium o wysokim współczynniku załamania w medium o niższym współczynniku załamania, kąt padania fal świetlnych staje się ważnym czynnikiem. Jeśli kąt padania wzrośnie powyżej określonej wartości (zależnej od współczynnika załamania światła obu mediów), osiągnie punkt, w którym kąt jest tak duży, że żadne światło nie jest załamywane w ośrodku o niższym współczynniku załamania światła.

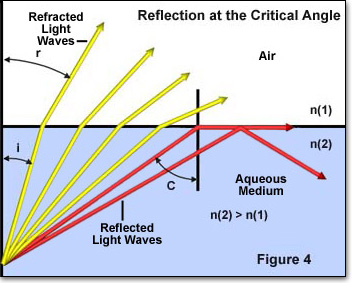
na rysunku 4 poszczególne promienie świetlne są reprezentowane przez czerwone lub żółte strzałki poruszające się od medium o wysokim współczynniku załamania (n(2)) do jednego o niższym współczynniku załamania (n(1)). Kąt padania każdego pojedynczego promienia światła jest oznaczony przez i, a kąt załamania przez r. wszystkie cztery żółte promienie światła mają kąt padania (i) wystarczająco niski, aby przejść przez interfejs między dwoma mediami. Jednak dwa promienie światła czerwonego mają kąty padania, które przekraczają kąt krytyczny (około 41 stopni) i są odbijane albo do granicy między mediami, albo z powrotem do ośrodka o wysokim współczynniku załamania światła. Zjawisko to ma miejsce, gdy kąt załamania światła (kąt r na rysunku 4) staje się równy 90 stopni, a prawo Snella zmniejsza się do:

gdzie (q) jest obecnie określany jako kąt krytyczny C. Jeśli medium o mniejszym współczynniku załamania światła jest powietrze (n = 1.00), równanie dodatkowo zmniejsza się do:

jak wspomniano wcześniej, inną ważną cechą załamania światła jest to, że długość fali światła ma wpływ na ilość załamania światła występującego w medium. W rzeczywistości ilość refrakcji, która ma miejsce, jest odwrotnie proporcjonalna do długości fali padającego światła. W ten sposób światło widzialne o krótszej długości fali jest załamywane pod większym kątem niż światło o dłuższej długości fali. W związku z tym, gdy białe światło, które składa się ze wszystkich kolorów w widmie widzialnym, jest przepuszczane przez szklany pryzmat, jest rozproszone na Kolory składowe w sposób zależny od indywidualnych długości fal. Światło widzialne o niskiej częstotliwości (600 nanometrów i więcej) jest załamywane pod mniejszym kątem niż światło o wyższej częstotliwości, co powoduje efekt podobny do tęczy, jak pokazano poniżej na rysunku 5.

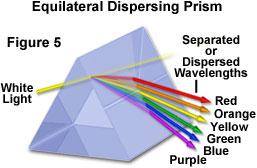
to samo zjawisko jest również odpowiedzialne za aberrację chromatyczną. Gdy białe światło jest przepuszczane przez prostą wypukłą soczewkę, w bliskiej odległości powstaje kilka punktów ogniskowych, które odpowiadają niewielkim różnicom współczynników załamania światła składowych długości fal. Efekt ten ma tendencję do tworzenia kolorowych (czerwonych lub niebieskich, w zależności od ostrości) aureoli otaczających obrazy obiektów. Korekcja tej aberracji jest zwykle dokonywana poprzez zastosowanie kombinacji dwóch lub więcej elementów soczewek złożonych z materiałów o różnych właściwościach dyspersyjnych, takich jak soczewka Achromatyczna zbudowana zarówno z okularów koronowych, jak i krzemiennych.

	Interactive Java Tutorial
załamanie przez pryzmat zbadaj, jak światło białe jest rozdzielane na Kolory składowe przez załamanie przez różne kąty w pryzmacie.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. Najczęstszym przykładem jest kamera, która jest zaprojektowana do tworzenia ostrych i skupionych obrazów na emulsji filmu lub powierzchni urządzenia sprzężonego z ładunkiem (CCD) w celu uzyskania dokładnego obrazu. Inne urządzenia optyczne wykorzystujące te cechy światła to mikroskopy i teleskopy, które umożliwiają oglądanie obiektów niewidocznych dla nieuzbrojonego ludzkiego oka, niezależnie od tego, czy znajdują się one na głowie szpilki, czy w odległej galaktyce.

autorzy

Mortimer Abramowitz – Olympus America, Inc., Two Corporate Center Drive., Melville, Nowy Jork, 11747.

Shannon H. Neaves and Michael W. Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., the Florida State University, Tallahassee, Florida, 32310.

powrót do światła i koloru

pytania lub komentarze? Wyślij do nas e-mail.

© 1998-2021 Michael W. Davidson i Florida State University. Wszelkie Prawa Zastrzeżone. Żadne obrazy, grafiki, skrypty ani aplety nie mogą być powielane ani wykorzystywane w jakikolwiek sposób bez zgody właścicieli praw autorskich. Korzystanie z tej strony oznacza, że zgadzasz się na wszystkie warunki prawne określone przez właścicieli.

ta strona jest utrzymywana przez nasz
zespół graficzny& zespół programistów internetowych
we współpracy z mikroskopią optyczną w
National High Magnetic Field Laboratory.

Ostatnia modyfikacja: piątek, 13 lis 2015 o 02:18 PM

Liczba dostępu od 10 marca 2003: 181405

odwiedź strony naszych partnerów w dziedzinie edukacji: