Prealgebra
efekty uczenia się
- Znajdź powierzchnię, podstawę i wysokość trójkąta
- Znajdź długość jednego boku trójkąta biorąc pod uwagę obwód i dwie inne długości
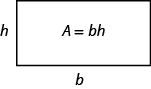
teraz wiemy, jak znaleźć powierzchnię prostokąta. Możemy użyć tego faktu, aby zwizualizować wzór na pole trójkąta. W prostokącie poniżej, oznaczyliśmy długość b i szerokość h, więc jego powierzchnia to bh.
pole prostokąta jest podstawą, B razy wysokość, h.
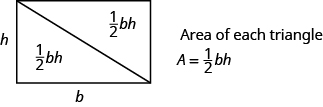
możemy podzielić ten prostokąt na dwa przystające trójkąty (patrz obrazek poniżej). Trójkąty przystające mają identyczne długości i kąty, więc ich obszary są równe. Pole każdego trójkąta jest połową pola prostokąta, czyli \frac{1}{2}bh. Ten przykład pomaga nam zrozumieć, dlaczego wzór na pole trójkąta to a = \frac{1}{2}bh.
prostokąt można podzielić na dwa trójkąty o równej powierzchni. Pole każdego trójkąta jest równe połowie pola prostokąta.
wzór na pole trójkąta to a=\frac{1}{2}bh, gdzie b jest podstawą, a h jest wysokością.
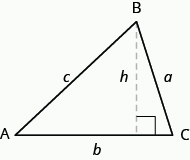
Aby znaleźć pole trójkąta, musisz znać jego podstawę i wysokość. Podstawą jest długość jednego boku trójkąta, Zwykle boku na dole. Wysokość jest długością linii, która łączy podstawę z przeciwległym wierzchołkiem i tworzy \text{90}^ \ circ kąt z podstawą. Poniższy obrazek przedstawia trzy trójkąty z zaznaczoną podstawą i wysokością każdego z nich.
wysokość H trójkąta jest długością odcinka linii, który łączy podstawę z przeciwległym wierzchołkiem i tworzy kąt \text{90}^ \circ z podstawą.
właściwości trójkąta
dla dowolnego trójkąta \Delta ABC suma miar kątów wynosi \text{180}^ \circ.
m\angle{a}+m\angle{B}+M\angle{C}=180^\circ
obwód trójkąta jest sumą długości boków.
p=a+b+c
pole trójkąta to połowa podstawy, B, razy wysokość, h.
a=\frac{1}{2}bh
przykład
znajdź pole trójkąta, którego podstawa wynosi 11 cali, a wysokość 8 cali.
rozwiązanie
| Krok 1. Przeczytaj problem. Narysuj figurę i oznacz ją podanymi informacjami. |  |
| Krok 2. Zidentyfikuj to, czego szukasz. | obszar trójkąta |
| Krok 3. Nazwisko. Wybierz zmienną, aby ją reprezentować. | Niech a = obszar trójkąta |
| Krok 4.Tłumacz.
napisz odpowiednią formułę. substytut. |
 |
| Krok 5. Rozwiąż równanie. | A=44 cale kwadratowe. |
| Krok 6. Sprawdź:
a=\frac{1}{2}bh 44\stackrel{?{ = } \ frac{1}{2}(11)8 44=44\checkmark |
|
| Krok 7. Odpowiedz na pytanie. | powierzchnia wynosi 44 cale kwadratowe. |
spróbuj
przykład
Obwód trójkątnego ogrodu wynosi 24 stopy. Długość dwóch boków wynosi 4 stopy i 9 stóp. Jak długa jest trzecia strona?
spróbuj
przykład
powierzchnia trójkątnego okna kościoła wynosi 90 metrów kwadratowych. Podstawa okna wynosi 15 metrów. Jaka jest wysokość okna?
spróbuj
równoramienne i trójkąty równoboczne
oprócz trójkąta prostokątnego, niektóre inne Trójkąty mają specjalne nazwy. Trójkąt o dwóch bokach jednakowej długości nazywany jest trójkątem równoramiennym. Trójkąt, który ma trzy boki równej długości, nazywa się trójkątem równobocznym. Poniższy obrazek pokazuje oba typy trójkątów.
w trójkącie równoramiennym dwa boki mają tę samą długość, a trzeci bok jest podstawą. W trójkącie równobocznym wszystkie trzy boki mają tę samą długość.
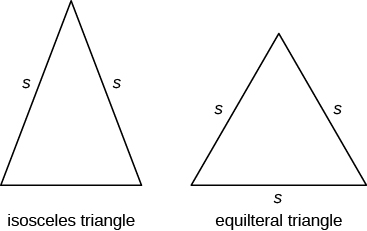
równoramienne i trójkąty równoboczne
trójkąt równoramienny ma dwa boki tej samej długości.
trójkąt równoboczny ma trzy boki jednakowej długości.
przykład
obwód trójkąta równobocznego wynosi 93 cale. Znajdź długość każdej strony.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. Chusta będzie trójkątem równoramiennym o podstawie
60 cali. Jak długo może zrobić dwie równe strony?








