31 maja 1832 roku od postrzału zmarł Francuski republikański rewolucjonista Évariste Galois. Miał 20 lat. Poprzedniej nocy, obawiając się własnej śmierci, Galois napisał wiele listów, frenetycznie pisząc: „nie mam czasu, nie mam czasu”. Jedna litera jest szczególnie cenna ze względów historycznych. W liście tym Galois twierdzi, że faktycznie wywołał rewolucję. Nie polityczne. Ale matematyczny.

zapoczątkowana przez Galois rewolucja okazała się większa i głębsza, niż mógłby sobie wyobrazić! Krajobraz matematyki został głęboko dotknięty przez wizję Galois, ponieważ jego potomstwo wzrosło i przejęło matematyczny świat. To potomstwo jest teraz wszechobecne i rządzi nieograniczonymi krainami. To idzie pod nazwą czystej algebry.

aby jeszcze bardziej urozmaicić opowieść o dramatycznym życiu Galois, oto streszczenie dokumentu, który zrobiłem o algebrze:

zdecydowanie jest! Ale jego rewolucja matematyczna nie poszła gładko. Jak wszyscy przywódcy rewolucji, najpierw miał największe trudności. Nie wyobrażać sobie rewolucji. Ale aby przekonać innych do przyłączenia się do niego w zmieniającym grę podejściu do matematyki. Kiedy Galois jeszcze żył, jego rewolucyjne idee zostały kilkakrotnie odrzucone przez Francuską Akademię Nauk … ponieważ najlepsi francuscy matematycy, tacy jak Siméon Denis Poisson, nie mogli tego zrozumieć! Częściowo z powodu nieczytelnego pisma Galoisa wyświetlanego po prawej stronie …

w 1843 roku, 10 lat po śmierci Galois, genialny francuski matematyk Joseph Liouville zdołał pojąć niektóre idee Galois. Po kolejnych trzech latach pracy, Liouville opublikował artykuł, aby je wyjaśnić. Ale artykuł Liouville ’ a był nadal zbyt naciągany, aby inni matematycy mogli się nim cieszyć i rozumieć. Kolejne 24 lata zajęło znalezienie francuskiego matematyka na tyle wybitnego, by lepiej zrozumieć Galois i uczynić jego idee przejrzystymi. Ten wybitny matematyk to Camille Jordan. W rzeczywistości książka Jordana z 1870 roku o teorii Galois była tak dobrze napisana, że niemiecki matematyk Felix Klein uznał ją za czytelną jak niemiecka książka!

To był zdecydowanie ogromny impuls. Ale potrzeba kolejnych 82 lat, aby wielki austriacki matematyk Emil Artin w końcu nadał teorii Galois swoją współczesną formę, w 1942 roku. Artin zasługuje na wiele kredytów. Podczas gdy Galois był wizjonerem, który przewidział tę rewolucję, Artin, pod wieloma względami, jest Tym, który faktycznie podjął rewolucję i obalił matematykę. Dzięki Artinowi i kilku innym, teoria Galois stała się nieuniknionym kamieniem węgielnym badań w matematyce, z mnóstwem zaskakujących i niesamowitych osiągnięć (jak dowód Wilesa na ostatnie twierdzenie fermata), a także ogromnym zbiornikiem otwartych pytań i tajemnic!

pola w czystej algebrze

teoria Galois dotyczy symetrii liczb. Ale zanim tam dotrę, muszę cię przedstawić, żeby cię uzbroić, dając ci sekret o liczbach. I jestem pewien, że o tym słyszałeś! Rzeczywiście, w liceum, prawdopodobnie nauczono cię nigdy nie zostawiać korzeni w mianownikach.

chodzi mi o to, że $1 / (\sqrt{2}-1)$ nie była prawidłową odpowiedzią. Czy możesz pomóc pozbyć się pierwiastka z 2 w mianowniku?

Hehe … nauczono nas mnożyć w górę i w dół Przez koniugat mianownika. Koniugat ten otrzymuje się przez zastąpienie $ – $ przez $ + $ (lub odwrotnie) w mianowniku:

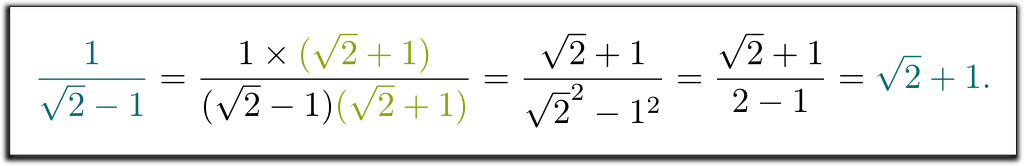
wiem! Skomplikowane wyrażenie $1/(\sqrt{2}-1)$ reprezentuje taką samą liczbę jak $\sqrt{2}+1$. I to wyjaśnia, dlaczego nasi nauczyciele chcieli, abyśmy pisali wyniki w taki sposób, a nie w inny sposób: kiedy wszystko jest napisane w ten sam sposób, egzaminy stają się o wiele łatwiejsze do skorygowania!

ale co z $1 / (\sqrt{2}-1)$? Możesz pozbyć się pierwiastka w mianowniku? Czy można to w ogóle zrobić?

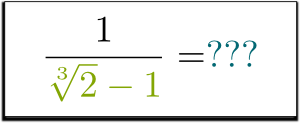
wiem!

ty mi powiedz!

poszczęściło się?

Hehe … co ciekawe, każda potęga $\sqrt{2}-1$ może być zapisana jako suma potęg $\sqrt{2}$. Rzeczywiście, wystarczy rozdzielić produkty:

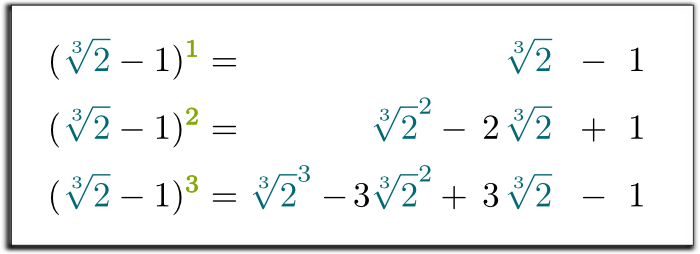
tak jest! Wykonując to podstawienie w trzecim równaniu, pokazaliśmy, że trzy pierwsze potęgi $\sqrt{2}-1$ można zapisać jako sumę liczby wymiernej, $\sqrt{2}$ i $\sqrt{2}^2$!

więc mamy teraz 3 równania, z 2 wyrażeniami pierwiastkowymi chcemy się pozbyć! W ten sposób możemy połączyć równania, aby usunąć wszystkie wyrażenia root po prawej stronie!

pomnóżmy 2 pierwsze linie przez 3 i zsumujmy wszystkie 3 równania:

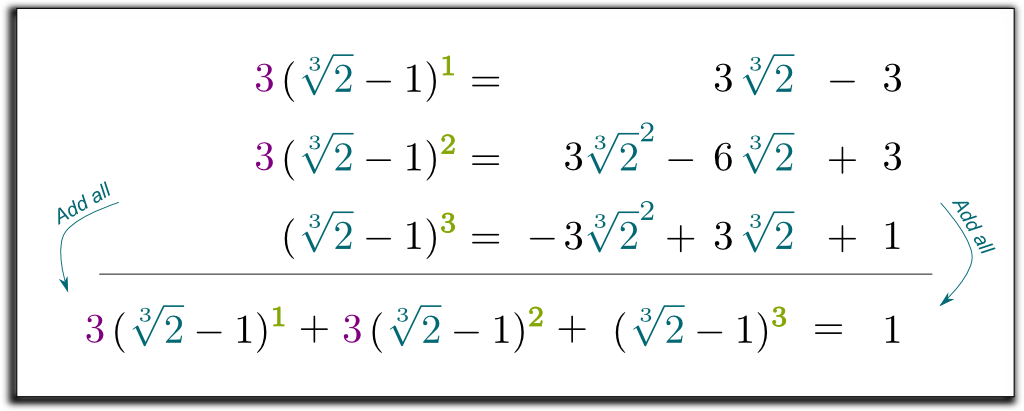
Hehe… najfajniejsze jest to, że lewy termin, który otrzymaliśmy, można teraz obliczyć przez $\sqrt{2}-1$! Pominę nudne obliczenia … i przejdę do wyniku $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Aby pozbyć się pierwiastków w mianowniku, możemy pomnożyć w górę i w dół przez $\sqrt{2}^2 + \sqrt{2} + 1$! Na koniec otrzymujemy następujący zaskakujący i piękny wzór:

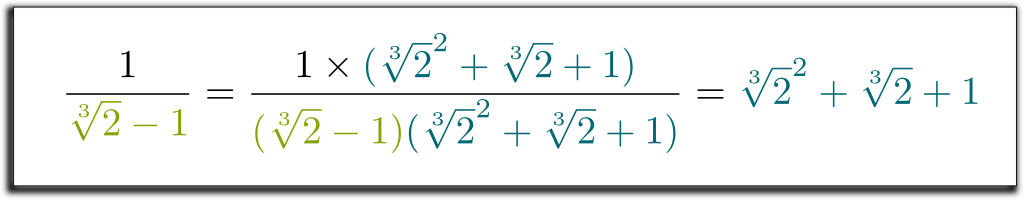
wiem! Ale to, co jest jeszcze ładniejsze, to to, że metoda, której użyliśmy, jest bardzo ogólna! Dzięki podobnej technice możemy teraz usunąć wszystkie rodniki z mianowników!

to, co szczególnie interesowało Galois, nie było faktem, że metoda umożliwiała usuwanie rodników z mianowników. Ale raczej, że każda liczba z rodnikami w mianownikach równa się liczbie z rodnikami na górze. Oznaczało to, że liczby z radykałami na górze były stabilne przez podział.

często oznacza się $\mathbb Q{2}]$ zbiór liczb, który można zapisać jako sumę potęg $\sqrt{2}$. Ponieważ $\sqrt{2}^3 = 2$ jest liczbą wymierną, każda suma potęg $\sqrt{2}$ może być zapisana w standardowej formie $a\sqrt{2}^2 + b\sqrt{2} + c$. Teraz, jeśli dodasz, odejmiesz lub pomnożysz dowolne dwie takie liczby, to nietrudno zauważyć, że otrzymujemy liczby, które nadal można umieścić w standardowej formie $a\sqrt{2}^2 + b\sqrt{2} + c$. Dodatkowo, pokazaliśmy tutaj, że odwrotność wszystkich liczb $a\sqrt{2}^2 + b\sqrt{2} + C$ może być również zapisana w standardowej formie. To pokazuje, że każde dodawanie, odejmowanie, mnożenie i dzielenie liczb w $\mathbb Q{2}]$ daje liczbę, która może być zapisana w standardowej formie… i dlatego należy do $\mathbb Q{2}]$. W czystej algebrze, $ \ mathbb Q{2}]$ jest więc stabilny przez cztery klasyczne operacje arytmetyczne. Z tego powodu nazywamy to polem.

Geometria rozszerzeń pól

pole, z którym jesteś najbardziej zaznajomiony, to prawdopodobnie zbiór $\mathbb Q$ liczb wymiernych. Innymi przykładami pól są zbiory $ \ mathbb R$ liczb rzeczywistych oraz zbiór $\mathbb C$ liczb zespolonych. A teraz mamy również $ \ mathbb Q{2}]$. Ponieważ $ \ mathbb Q{2}]$ jest polem zawierającym pole $ \ mathbb Q$, mówimy, że $\mathbb Q{2}] / \mathbb Q$ jest rozszerzeniem pola.

fakt, że $\mathbb Q{2}] / \mathbb Q$ jest rozszerzeniem pola, daje bardzo naturalny związek między tymi dwoma polami. Mianowicie, $ \ mathbb Q{2}]$ może być postrzegane jako przestrzeń wektorowa, gdzie $\mathbb Q$ jest polem skalarnym. W szczególności, fakt, że dowolną liczbę w $\mathbb Q{2}]$ można zapisać $a \sqrt{2}^2 + b\sqrt{2} + c$ oznacza, że $(1, \sqrt{2}, \sqrt{2}^2)$ tworzy podstawę $\mathbb Q{2}]$ jako $\mathbb Q$-przestrzeń wektorowa. A to oznacza, że możemy przedstawić ją geometrycznie jako 3-wymiarową przestrzeń!

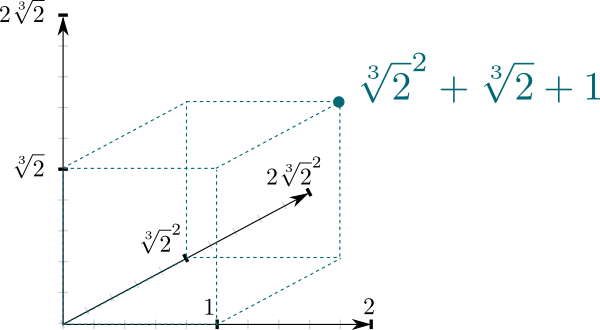
wymiar powyższej przestrzeni wektorowej jest interesującą właściwością rozszerzeń pól. Jest znany jako stopień i jest powszechnie oznaczany $ \ big{2}]: \ mathbb Q\big] = 3$ na przykład.

tak! W rzeczywistości bardzo łatwo jest utworzyć rozszerzenie tego pola: wystarczy dodać liczbę radykalną, która nie należy do $ \ mathbb Q{2}]$!

tak! Spowoduje to utworzenie pola $(\mathbb Q{2}]) = \mathbb Q{2}, \ sqrt{2}]$. Pola te zawierają wszystkie liczby będące produktami i sumami $\sqrt{2}$ i $\sqrt{2}$. Mają one postać $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ D\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Masz pojęcie, jaki jest stopień $\big{2}, \sqrt{2}] : \mathbb Q{2}]\big]$?

tak! W rzeczywistości mamy $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ D\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e \sqrt{2} + f) \sqrt{2}$. Tak więc dowolną liczbę $\mathbb Q{2},\sqrt{2}]$ można zapisać $A+B\sqrt{2}$, Gdzie $a$ i $B$ należą do $ \ mathbb Q{2}]$. Zatem 2 Skalary $ \ mathbb Q{2}]$ określają liczbę w $\mathbb Q{2},\sqrt{2}]$. Oznacza to, że stopień rozszerzenia pola $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ wynosi 2. W rzeczywistości mamy relację Chaslesa $ \ big{2}, \sqrt{2}] : \mathbb Q \big] $=$ \big{2}, \sqrt{2}] : \ mathbb Q{2}] \big] \big{2}] : \mathbb Q \big] $=$ 2 \razy 3 = 6$.

jest lepiej! Każde rozszerzenie pola o skończonym stopniu, zwane skończonym rozszerzeniem pola, jest rozpięte przez pojedyncze liczby. Na przykład $\mathbb Q{2}, \sqrt{2}] $ = $ \mathbb Q{2} + \sqrt{2}]$, co oznacza, że wszystkie liczby będące sumami potęg $\sqrt{2}$ i $\sqrt{2}$ są również sumami potęg $\sqrt{2} + \ sqrt{2}$. Czy to nie jest zaskakująco niesamowite?

ogólnie rzecz biorąc, każde skończone rozszerzenie pola $\mathbb Q$ można zapisać $\mathbb Q$ z pewnym $x$, które jest dodawane do $\mathbb Q$.

tak. Dotyczy to rozszerzenia pola $ \ mathbb R / \ mathbb Q$. I tak jest najważniejsze rozszerzenie pola w teorii Galois! To rozszerzenie pola to $ \ bar {\mathbb Q} / \ mathbb Q$, gdzie $ \ bar{\mathbb Q}$ jest zbiorem liczb algebraicznych. Są to wszystkie rozwiązania równań wielomianowych postaci $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $ + $ a_0 = 0$. Na przykład $\sqrt{2}$ jest liczbą algebraiczną, ponieważ jest rozwiązaniem $x^4-2x = 0$. Zatem $ \ bar {\mathbb Q}$ jest rozszerzeniem pola do wszystkich skończonych rozszerzeń pola $ \ mathbb Q$.

liczby sprzężone

już prawie jesteśmy! Musimy przejść przez równania wielomianowe.

dokładnie! Galois zauważył, że niektóre równania można uprościć. Na przykład, $x^4-2x=0$ może być obliczone jako $x (x^3-2)=0$, co odpowiada $x=0$ lub $x^3-2=0$. Zatem równanie $x^4-2x=0$ może być zredukowane do równań $x=0$ i $x^3-2=0$. I w rzeczywistości, ta redukcja jest bardzo podobna do tego, jak liczby takie jak 35 mogą być zredukowane do 5 i 7, ponieważ $5 \razy 7 = 35$. Podobieństwo między równaniami i liczbami całkowitymi jest tak silne, że możemy nawet tworzyć euklidesowe podziały wielomianów, tak jak nauczyłeś się tego dla liczb! Po prawej jest przykład takiego podziału (nie martw się, jeśli go nie rozumiesz, nie będzie to ważne dla kontynuacji).

dokładnie! Są one znane jako nieredukowalne równania wielomianowe. Równanie $x^3-2=0$ jest przykładem nieredukowalnego równania wielomianowego.

tak! Ale co najważniejsze, Galois chciał skupić się na równaniach o współczynnikach wymiernych. Lub raczej wielomiany o współczynnikach, które należą do pola bazowego. Chodziło mi o to, że dla $ \ mathbb Q$ jako pola podstawowego, $x^3-2=0$ jest nieredukowalne.

rozważmy $x^2 – 2x -1=0$, aby mieć jakieś wskazówki. Równanie to można udowodnić jako nieredukowalne. Pamiętasz, jak to rozwiązać?

If $b^2-4AC \ geq 0$, yes.

dokładnie! Więc nieredukowalne równanie wielomianowe $x^2 + 2x -1 = 0$ ma dwa rozwiązania: $1 + \sqrt{2}$ i $1 – \sqrt{2}$ … jakiś komentarz?

Bingo! To kluczowe odkrycie Galois. Bardziej ogólnie, Galois nazywa koniuguje wszystkie rozwiązania do nieredukowalnego równania wielomianowego. I, jak można sobie wyobrazić, są one niezbędne do usunięcia rodników z mianowników!

pierwszą rzeczą, którą należy zauważyć, jest to, że jeśli $x_1$, $x_2$,…, $x_n$ są rozwiązaniami wielomianu nieredukowalnego równania $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ przy współczynnikach wymiernych, to to wielomianowe nieredukowalne równanie może zostać przepisane $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Identyfikacja stałych daje $x_1 x_2 … x_n $ = $ (-1)^N a_0 / a_n$. Tak więc, co najważniejsze, iloczyn liczb sprzężonych jest liczbą wymierną $(-1)^N a_0/a_n$, która jest niezerowa(udowodnij to!).

oto mały żart, aby pamiętać o silnym związku między koniugatami:

rozważmy ułamek $1 / x_1$, gdzie $x_1$ jest skomplikowanym wyrażeniem z rodnikami. Mnożenie w górę i w dół przez koniugaty $x_2$,…, $x_n$ z $x_1$ daje $1 / x_1 $ = $ (-1)^N a_n x_2…x_n / a_0$, który nie ma pierwiastka w mianowniku, ponieważ ustaliliśmy, że $a_0$ jest niezerową liczbą pola podstawowego!

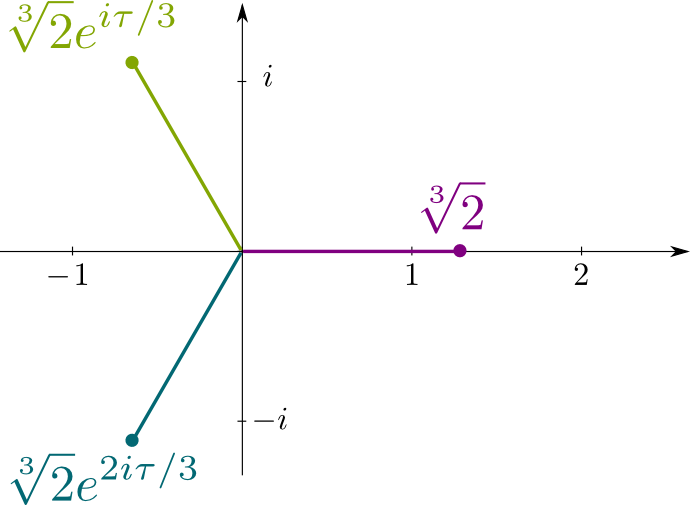
Przypomnijmy, że $x^3-2=0$ jest nieredukowalnym równaniem wielomianowym $\sqrt{2}$ jest rozwiązaniem. Więc jego koniugaty są innymi rozwiązaniami tego równania, które są liczbami zespolonymi $\sqrt{2} j$ i $\sqrt{2} j^2$, gdzie $j= E^{i\tau/3}$ z $\tau = 2\pi$ jest stosunkiem obwodu okręgu przez jego promień. Poniższy rysunek pokazuje położenie sprzężonych rozwiązań na tej płaszczyźnie zespolonej:

dwuznaczność Galois

wreszcie, przechodzimy do kluczowego wglądu Galois!

koniugaty są doskonale permutowalne. Oznacza to, że jeśli systematycznie zmienisz $\sqrt{2}$ przez jego koniugat $-\sqrt{2}$, to równania nadal się utrzymują. Na przykład, ponieważ mieliśmy $1/(\sqrt{2}-1) = \sqrt{2}+1$, Mogę wprost powiedzieć, że $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! Podobnie mamy następujące implikacje:

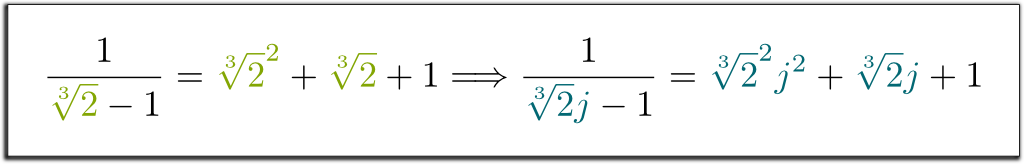
Hehe … przypomnę najpierw, że pola skończone są rozpięte przez pojedynczy element. Tak więc, jeśli pole bazowe to $ \ mathbb Q$, Każde skończone pole można zapisać $ \ mathbb Q$ dla jakiegoś prawego $x_1$. Rozważmy teraz $x^n + a_{n-1}x^{n-1} $ + $ … + a_1 x + a_0 = 0$ nieredukowalne równanie wielomianowe $x_1$ jest rozwiązaniem. Następnie, co definiuje $ \ mathbb Q$ to$ \ mathbb Q $ -przestrzeń wektorowa rozpięta przez $x_1$, $x_1^2$,…, $x_1^{n-1}$, z uproszczeniem większych potęg $x_1$ zgodnie z algebraiczną zasadą $x_1^n $ = $ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

dokładnie! Co najważniejsze, te algebraiczne reguły $ \ mathbb Q$ tak naprawdę nie zależą od Natury $x_1$; zależą tylko od nieredukowalnego wielomianu $x_1$ jest rozwiązaniem! Dlatego reguły $\mathbb Q$ są identyczne z regułami $ \ mathbb Q$,…, $\mathbb Q$, gdzie $x_1$ jest zastępowane przez jeden z koniugatów $x_2$,…, $x_n$. W szczególności pola $ \ mathbb Q{2}]$ i $\mathbb Q{2} j]$ działają zgodnie z dokładnie tymi samymi regułami. Dlatego koniugaty są doskonale permutowalne! Mówimy, że pola $\mathbb Q{2}]$ i $\mathbb Q{2} j]$ są izomorficzne, a zastąpienie $\sqrt{2}$ przez $\sqrt{2}j$ jest izomorfizmem $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

w bardzo podobny (ale silniejszy) sposób, że dwie przestrzenie wektorowe wymiaru 2 są mniej więcej takie same! To ma straszne konsekwencje. Oznacza to, że z algebraicznego punktu widzenia nie ma sensu robić różnicy między liczbą a którymkolwiek z jej koniugatów (o ile systematycznie zastępujesz liczbę jej koniugatem)! Na przykład $\sqrt{2}$ i $ – \sqrt{2}$ są algebraicznie nierozróżnialne! Aby mieć to na uwadze, oto kolejny żart, który wymyśliłem:

wcale nie! Każde rozróżnienie między tymi dwoma liczbami musi obejmować jakąś inną matematykę niż algebra, jak relacje porządkowe czy topologia. Chodzi mi o to, że na przykład relacja $\sqrt{2} > 0$ robi różnicę między $\sqrt{2}$ przez $-\sqrt{2}$, ale to dlatego, że wiąże się z relacją zamówienia. Ale jeśli ograniczymy się do równań wielomianowych, to nie ma absolutnie żadnej różnicy między $\sqrt{2}$ i $ – \sqrt{2}$. Podobnie, $i$ I $ – i$, rozwiązania nieredukowalnego równania wielomianowego $x^2+1 = 0$, są również algebraicznie nierozróżnialne. Jednak arbitralnie nazywamy $i$ jednym z nich. Dlatego Galois nazwał swoją teorię teorią dwuznaczności. Dzisiaj dwuznaczność wyboru konwencjonalnego pierwiastka kwadratowego z $-1$ pomiędzy $i$ I $ – i$ nazywa się raczej symetrią pomiędzy $i$ I $-i$.

Galois grupy

Galois szczególnie koncentruje się na rozszerzeniach pól, które są stabilne przez koniugację. Takie stabilne rozszerzenia pól są obecnie znane jako rozszerzenia Galois. Jeśli więc $x_1$ należy do rozszerzenia Galois, to to rozszerzenie Galois zawiera wszystkie jego koniugaty $x_2$,…, $x_n$.

prosty sposób konstruowania rozszerzeń Galois polega na wzięciu pola rozplanowanego przez rozwiązania nieredukowalnego równania wielomianowego. Na przykład, jeśli $x_1$,…, $x_n$ są koniugatami dla pola podstawowego $ \ mathbb Q$, to $ \ mathbb Q / \ mathbb Q$ jest rozszerzeniem Galois. Tak skonstruowane pola nazywane są polami dzielącymi.

na przykład pole podziału równania $x^3-2=0$ jest rozszerzeniem Galois $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$.

Jeśli $x_1$ obejmuje rozszerzenie Galois, to także jego koniugaty. Tak więc, $ \ mathbb Q = \ mathbb Q = $ … $ = \ mathbb Q$ = $ \ mathbb Q$. Zatem izomorfizm pomiędzy $ \ mathbb Q$ i $ \ mathbb Q$, który polega na zastąpieniu zawsze $x_1$ przez $x_2$, jest w rzeczywistości izomorfizmem między $\mathbb Q$ A samym sobą! Nazywamy to automorfizmem. Automorfizmy rozszerzenia Galois $ \ mathbb Q / \ mathbb Q$ tworzą grupę Galois $gal (\mathbb Q/ \ mathbb Q)$.

teraz, co najważniejsze, jeśli $ \ mathbb Q = \ mathbb Q$, to wszystkie automorfizmy rozszerzenia Galois $ \ mathbb Q / \mathbb Q$ są permutacjami $x_1$ z jednym z jego koniugatów! W szczególności widzimy tutaj, że cardinalność grupy Galois jest równa stopniowi rozszerzenia Galois.

pewnie! Można zauważyć, że $ \ mathbb Q = \ mathbb Q$ i $ \ mathbb Q = \ mathbb Q$, co oznacza, że $I$ i $\sqrt{2}$ każdy obejmuje pola dzielenia nieredukowalnego równania wielomianowego, którego są rozwiązaniem. Tak więc, $ \ mathbb Q / \ mathbb Q$ i $ \ mathbb Q / \ mathbb Q$ są rozszerzeniami Galois. Dlatego ich automorfizmy polegają na zastąpieniu $i$ przez jeden z jego koniugatów, $i$ lub $ – I$ i zastąpieniu $\sqrt{2}$ przez $\sqrt{2}$ lub $-\sqrt{2}$. W pierwszych przypadkach nic nie zmieniamy na liczby, co odpowiada symetrii zerowej. Drugi przypadek można zwizualizować jako symetrie osiowe, jak pokazano na poniższym rysunku:

czy to nie niesamowite?

pewnie! Przejdźmy do pola dzielenia $\mathbb Q{2}, \ sqrt{2}j, \sqrt{2} j^2]$ z $x^3-2=0$. Ale zanim przejdziemy dalej, zauważmy, że $\mathbb Q{2}, \sqrt{2}j, \sqrt{2}j^2] = \ mathbb Q{2}, j]$.

wszystko, co musimy udowodnić, to to, że wszystkie generatory jednego pola należą do drugiego. Zacznijmy od udowodnienia, że generatory tego drugiego, $\sqrt{2}$ I $j$, należą do pierwszego. To oczywiste dla $\sqrt{2}$. Teraz, $j = (\sqrt{2} j) / \sqrt{2}$, więc $j$ należy również do poprzedniego pola. Dowodzi to, że wszystkie elementy $\mathbb Q{2},j]$ należą do $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Podobnie, jest oczywiste, że wszystkie generatory poprzedniego pola, $\sqrt{2}$, $\sqrt {2} j$ i $\sqrt{2} j^2$, są produktami generatorów tego drugiego. Tak więc oba pola są równe. W szczególności, $ \ mathbb Q{2}, j] / \ mathbb Q$ jest rozszerzeniem Galois.

Hehe… aby zrozumieć symetrie $\mathbb Q{2}]$, musimy pójść dalej w badaniu grup Galois…

korespondencja Galois

problem z grupami Galois polega na tym, że mogą stać się bardzo duże i skomplikowane. Jest to szczególnie przypadek nieskończonej grupy $gal (\bar {\mathbb Q}/ \ mathbb Q)$. Aby uchwycić tak wielkie i złożone grupy, Galois wpadł na genialny pomysł, aby rozbić je na mniejsze kawałki.

o dziwo, Galois odkrył, że grupy Galois można podzielić na podgrupy symetrii, patrząc tylko na te, które pozostawiają pewne subfield niezmienione. Na przykład, $ \ mathbb Q$ jest polem podrzędnym $ \ mathbb Q{2}, j]$, ponieważ każda liczba pierwszej należy do drugiej. Tak więc symetrie $ \ mathbb Q{2},j]$, które niczego nie zmieniają na $\mathbb Q$ tworzą podgrupę grupy Galois $\mathbb Q{2}, j]/\mathbb Q$. Te symetrie tworzą grupę Galois $gal (\mathbb Q{2},j]/ \ mathbb Q)$.

wiem! Lubię wizualizować te symetrie jako sposoby podłączenia $ \ mathbb Q{2}, j]$ do $ \ mathbb Q$. Oto obraz „podłączenia do”:

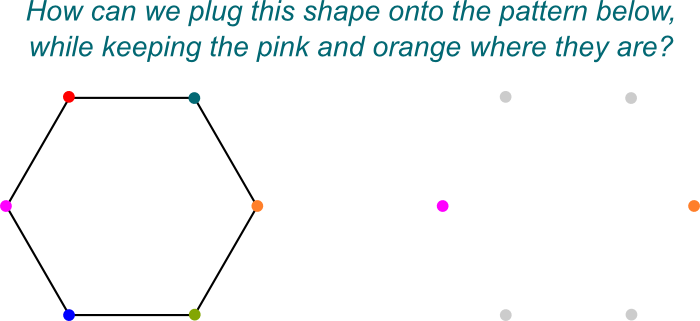
dokładnie! A to dlatego, że $ \ mathbb Q{2}, j]$ jest rozszerzeniem Galois $ \ mathbb Q$ , które samo w sobie jest rozszerzeniem pola $\mathbb Q$.

i nie tylko! Galois pokazał, że wszystkie podgrupy rozszerzeń Galois są otrzymywane w ten sposób! Dokładniej, odwzorowanie dowolnego pola $K$ pomiędzy rozszerzeniem Galois $ \ mathbb Q{2}, j]$ a polem bazowym $ \ mathbb Q$ do grupy Galois $gal (\mathbb Q{2},j] / K)$ jest bijektywne. Ten fakt nazywa się korespondencją Galois! Ta korespondencja jest schematycznie wyświetlana poniżej dla rozszerzenia Galois $ \ mathbb Q / \ mathbb Q$.

zamiast próbować opisywać tę grupę bezpośrednio, skupmy się na jej podgrupie $gal(\mathbb Q{2}, j]/\mathbb Q)$. To proste, że $\sqrt{2}$ obejmuje $\mathbb Q{2},j]$ Po dodaniu do $\mathbb Q$. Tak więc, $\mathbb Q{2},j]/\mathbb Q$ jest rozszerzeniem Galois rozciągniętym przez $ \ sqrt{2}$. Dlatego, korzystając z twierdzenia, które widzieliśmy wcześniej, wiemy, że wszystkie automorfizmy tego rozszerzenia Galois polegają na zastąpieniu $\sqrt{2}$ przez jeden z jego 3 koniugatów(sam, $\sqrt{2} j$ i $\sqrt{2} j^2$)!

teraz mógłbym dalej studiować inne elementy $gal(\mathbb Q{2}, j]/\mathbb Q)$, jak podgrupa Galois $gal(\mathbb Q{2}, j] / \mathbb Q{2}])$. Ale wolę użyć innego z potężnych twierdzeń Galois. Mianowicie udowodnił, że jeśli $ \ mathbb Q / \ mathbb Q$ jest dodatkowo rozszerzeniem Galois, to podgrupa $gal (\mathbb Q{2}, j]/\mathbb Q)$ jest normalna.

zatem Grupa Galois $ \ mathbb Q{2}, j] / \ mathbb Q$ może być ilorazowana przez tę podgrupę, a grupa ilorazowa równa się wtedy $gal (\mathbb Q/ \ mathbb Q)$. Jednak, $ \ mathbb Q / \ mathbb Q$ jest rzeczywiście rozszerzeniem Galois rozciągniętym przez $j$, którego koniugat to $j^2$. Tak więc, $gal (\mathbb Q/ \ mathbb Q) $ polega na pozostawieniu $j$ jako $j$ lub zastąpieniu go $j^2$.

możemy teraz wydedukować wszystkie symetrie $gal(\mathbb Q{2},j]/\mathbb Q)$ poprzez połączenie tych $Gal(\mathbb Q{2},j] / \mathbb Q)$ i $Gal(\mathbb Q/\mathbb Q)$. Możemy wyświetlić te symetrie, rysując, jak wpływają one na nasze trzy koniugaty rozpinające $\sqrt{2}$, $\sqrt{2}j$ i $\sqrt{2}j^2$:

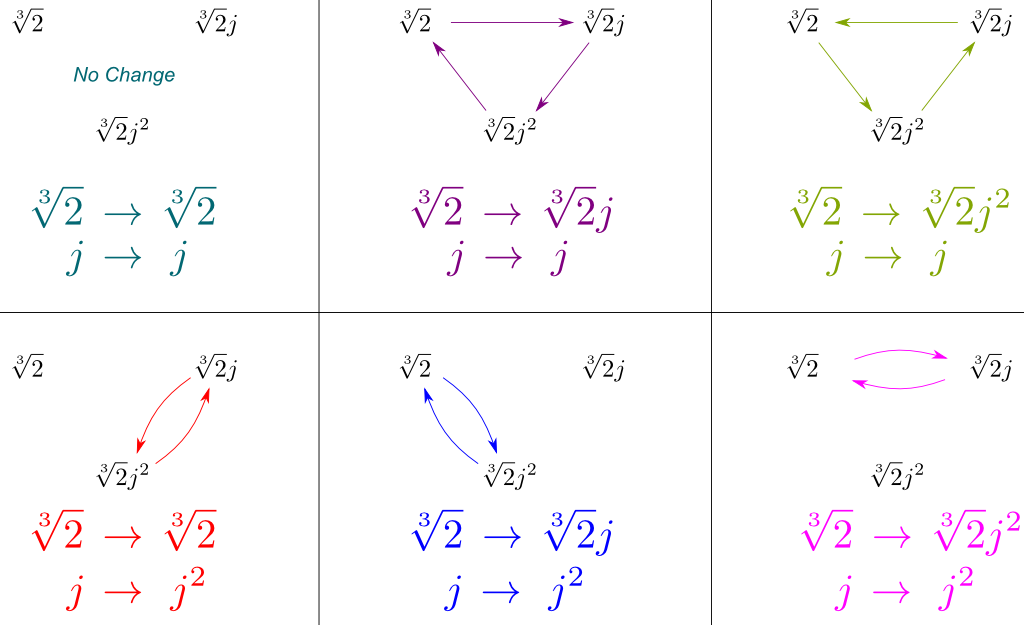
co najważniejsze, powyższy rysunek zawiera wszystkie symetrie $gal (\mathbb Q{2},j]/\mathbb Q)$. I o dziwo, te symetrie odpowiadają dobrze znanej grupie symetrii.

I ’ ll let Marcus du Sautoy present it to you:

czy symetrie są tu jak Rozgwiazda czy jak trójkąt?

tak, rzeczywiście! Ta grupa symetrii trójkąta nazywa się $D_3$ i jest taka sama jak grupa $S_3$ permutacji 3 elementów. To prowadzi nas do następującego wzoru, który uważam za tak piękny, że zdecydowałem się go oprawić!

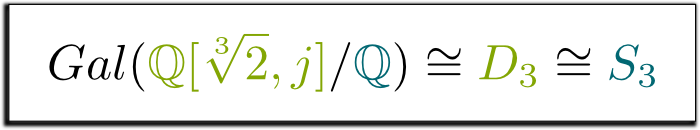
zakończmy

pod wieloma względami Galois należy uważać za ojca współczesnej algebry. Jego kluczowym spostrzeżeniem było spojrzenie na matematykę pod kątem zasad działania, co doprowadziło go do odkrycia zaskakujących i wnikliwych dwuznaczności lub symetrii między liczbami. Z algebraicznej perspektywy, liczby takie jak $\sqrt{2}$, $\sqrt{2}j$ i $\sqrt{2}j^2$ są w rzeczywistości idealnie symetryczne i całkowicie wymienne.

zrozumienie tych symetrii miało zadziwiające zastosowania m.in. w geometrii algebraicznej i topologii algebraicznej. W szczególności wczesne sukcesy teorii obejmują klasyfikację konstruktywnych wielokątów regularnych i twierdzenie, że równania wielomianowe wysokiego stopnia nie mogą być rozwiązane przez rodniki.

ostatnie sukcesy pojawiają się w kryptografii i dowodzie Andrew Wilesa na ostatnie twierdzenie Fermata. Dowód ten polega na badaniu grupy Galois $gal(\bar{\mathbb Q} /\mathbb Q)$ z reprezentacją grupy. Ale powiedziałbym, że teoria jest w jakiś sposób jeszcze młoda i wiele pozostaje do odkrycia. W końcu jest to jeden z najbardziej aktywnych obszarów badań w dzisiejszych badaniach czystej matematyki.

to powinno skłonić nas do oddania o wiele więcej hołdu niewiarygodnemu geniuszowi Galois … pozwolę sobie dodać jeden przez SocraticaStudios.