integralną częścią dynamiki płynów jest vorticity. Heurystycznie mierzy lokalny obrót paczki płynnej. W przypadku obiektów stałych nie mówimy o wirowości obiektu, lecz o jego prędkości kątowej. Te dwa pojęcia są ze sobą powiązane, ale wirowość jest bardziej przydatna przy omawianiu obracających się obiektów, które odkształcają się, tak jak robi to płyn.

wirowość danego pola prędkości w obrębie danej płaszczyzny jest obliczana przez wybranie dowolnych dwóch osi ortogonalnych w tej płaszczyźnie i dodanie prędkości kątowej każdej osi. W przypadku obiektu stałego lub płynu, który obraca się jak obiekt stały (trafnie nazywany obrotem ciała stałego), wir jest dwukrotnie większy od prędkości kątowej, ponieważ każda oś obraca się z taką samą szybkością. Jednak w płynie dwie osie mogą obracać się z bardzo różnymi szybkościami, a nawet w różnych kierunkach! Jest nawet możliwe, że każda oś może się obracać, ale wir netto jest zerowy (patrz wir irrotacyjny).

Jeśli ruch płynu jest ściśle ograniczony do leżenia w płaszczyźnie, to przyjmuje się, że wektor wiryczności jest prostopadły do płaszczyzny i nie może zmieniać kierunku (lub pochylenia). Jedynym aspektem wiryczności, który może się zmienić, jest jej wielkość. Uważa się, że ten transfer energii do większych skal jest związany z powstaniem Wielkiej Czerwonej Plamy na Jowiszu.

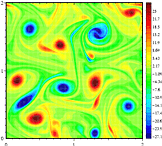
w trójwymiarowym ruchu płynów wektor wiryczności jest trójwymiarowy, ponieważ ma składniki równoległe do każdej osi, x, y i z: Składnik z jest równoległy do osi Z i opisuje szybkość obrotu w płaszczyźnie xy. To właśnie z powodu tej dychotomii istnieje jakościowa różnica w zachowaniu między turbulencją dwuwymiarową a turbulencją trójwymiarową. W pierwszym z nich istnieje tendencja do zlepiania się wirów i tworzenia większych wirów, podczas gdy w drugim ruchy wirowe są rozrywane, a energia spływa kaskadowo do najmniejszych skal, gdzie jest następnie rozpraszana.

matematycznie, wirowość danego pola prędkości,

jest zdefiniowana jako zwinięcie pola prędkości i jest zwykle oznaczana grecką literą omega,

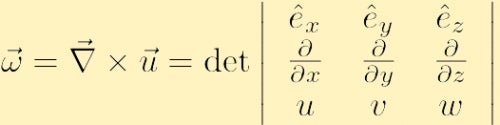
gdzie użyliśmy konwencjonalnego symbolu nabla dla gradientu:

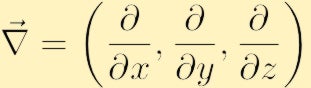
w postaci składowej wirytyczność znajduje się poprzez rozszerzenie powyższego wyznacznika,

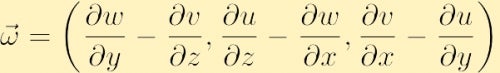
innym ważnym aspektem dynamiki płynów, który jest związany z wirytycznością, jest cyrkulacja. W przeciwieństwie do woryczności, która jest własnością lokalną, zdefiniowaną w każdym punkcie przestrzeni, cyrkulacja jest własnością globalną, zdefiniowaną przez całkowanie własności płynu po krzywej. W szczególności, jeśli wybierzesz dowolny zamknięty kontur i oznaczysz go literą C(t), cyrkulacja wokół C(T), w kierunku przeciwnym do ruchu wskazówek zegara, jest wielkością skalarną oznaczoną,

jest zdefiniowana jako,

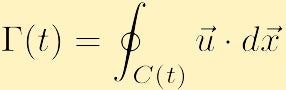
która może być funkcją czasu, podobnie jak zamknięty kontur.

poświęćmy chwilę, aby wyjaśnić, co to mówi fizycznie. W każdym punkcie konturu (t) znajdujemy składową prędkości, która jest styczna do krzywej i mnożymy ten Skalar przez nieskończoną długość; rzutowanie prędkości na styczną koniecznie da wielkość między prędkością w tym położeniu a zerem. Jeśli prędkość jest styczna do krzywej, otrzymujemy plus lub minus prędkość, jeśli prędkość jest prostopadła do krzywej, otrzymujemy zero. Następnie łączymy tę ilość, inaczej mówiąc sumując nieskończoną liczbę rzeczy, wokół konturu tak, że dodajemy wkład z każdego punktu. Na tej podstawie stwierdzamy, że cyrkulacja wzdłuż konturu C (t) jest wielkością przepływu wokół konturu C (t); wynik dodatni lub ujemny odpowiada odpowiednio cyrkulacji zgodnie z ruchem wskazówek zegara lub zgodnie z ruchem wskazówek zegara. Jednym z ekstremalnych przypadków jest sytuacja, w której pole prędkości jest wszędzie prostopadłe do krzywej C(t) i w konsekwencji nie występuje cyrkulacja, ponieważ przepływ zawsze przekracza kontur i nigdy nie płynie wzdłuż konturu. Aby uzyskać cyrkulację niezerową, musi istnieć pewna część krzywej, w której przepływ jest wzdłuż zamkniętego konturu.

Jeśli pole prędkości jest gładkie i nie ma osobliwości w C(t), możemy użyć twierdzenia całkowego Stokesa z rachunku wektorowego, aby przepisać cyrkulację jako,

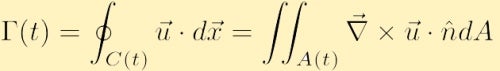
gdzie A jest obszarem zawartym w konturze C, a ń jest jednostkowym wektorem normalnym do obszaruaa.

zanim rozważymy to nowe równanie dla obiegu, warto zrozumieć znaczenie fizyczne dla twierdzenia Stokesa, gdzie pole wektorowe jest prędkością. W powyższej podwójnej całce obliczamy wir w każdym punkcie konturu, a następnie sumujemy wir we wszystkich tych punktach w A (t). W całce pojedynczej nad konturem zamkniętym obliczamy przepływ wzdłuż granicy obszaru. Twierdzenie Stokesa stwierdza wtedy, że te wielkości są równe, a zatem, że jeśli istnieje średnia wirowość w obrębie obszaru, co musi oznaczać, że obszar ma niezerową szybkość rotacji, w konsekwencji musi istnieć cyrkulacja netto wzdłuż obwodu tej granicy.

z twierdzenia o wartości średniej rachunku różniczkowego możemy zastąpić całkę w całce podwójnej wartością średnią, która odpowiada średniej składowej wiryczności prostopadłej do płaszczyzny, w której leży C(t). Druga interpretacja cyrkulacji polega więc na tym, że jest to średnia wirowość razy obszar zawarty w C(t). Zamiast obliczać cyrkulację na zamkniętym konturze C(t) możemy obliczyć średnią wirowość normalną do A(t) i pomnożyć ją przez obszar wewnątrz. Jeśli wziąć pod uwagę szczególny przypadek, w którym wir jest wszędzie stały, cyrkulacja będzie wielkością wiru razy obszar zawarty w środku.

wir punktowy to wir, który nie ma obszaru, co oznacza, że wir występuje tylko w jednym punkcie. Aby zbadać wiry punktowe, najpierw założymy, że mamy przepływ niezrozumiały 2D. (Wiry punktowe są czasami nazywane wirami liniowymi, gdy są oglądane W 3D.)

po pewnych obliczeniach ustalamy, że pole prędkości generowane przez wir punktowy w postaci złożonej, który znajduje się w z0, jest podane przez (Gdzie Gamma zero to cyrkulacja wokół wiru punktowego, która jest często określana jako siła wiru punktowego):

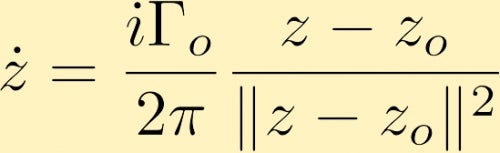
pole prędkości generowane przez wir punktowy może spowodować ruch innego wiru punktowego. Oto kilka przykładów tego: Dwa wiry punktowe, zarówno dodatnie, jak i równe, dwa wiry punktowe, oba dodatnie, ale jeden ma potrójną siłę drugiego, a jeden wir punktowy jest ujemny z dwukrotną wielkością drugiego, który jest dodatni . Inną możliwością jest rozważenie dwóch wirów punktowych o tej samej wielkości, ale przeciwnych znakach.

można to rozszerzyć na dowolną liczbę wirów punktowych, N. równanie ruchu w postaci zespolonej dla wiru punktowego alfa jest podane przez:

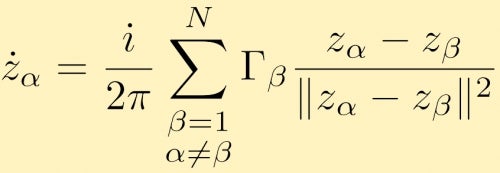
spojrzenie na interakcje wirów punktowych jest bardzo interesującym problemem, który jest trudny do wykonania analitycznie, szczególnie ze względu na wzrost liczby wirów punktowych. Symulacje numeryczne oddziaływań wirów punktowych są więc bardzo powszechne. Jednym z użytecznych zastosowań symulacji dużych wirów punktowych jest obserwacja dużych skupisk wirów punktowych, które symulują wiry o skończonej powierzchni. Oto opisy i wyniki kilku dużych symulacji wirów punktowych. W tym przypadku mamy dwa duże skupiska wirów punktowych o jednakowej sile łączących się. W następnym przypadku zaczynamy od pierścienia skupionych wierzchołków.

aby znaleźć równanie ewolucji wiryczności, zaczynamy od równania pędu. W równaniu pędu termin adwektywny można przepisać w następujący sposób,

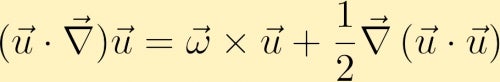
następnie obliczamy zwijanie równania pędu i poprzez niektóre tożsamości wektorowe otrzymujemy równanie wirowości:

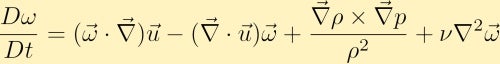
równanie wiryczności pokazuje, jak można generować wiryczność w płynie. Bez utraty ogólności przyjmiemy, że początkowo mamy tylko wirowość w kierunku Z. Z tego możemy zobaczyć, jak każde z czterech różnych określeń może zmienić wirowość.

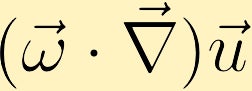
Jeśli istnieje zmiana prędkości z kierunkiem istniejącej wiryczności, można wygenerować wiryczność.

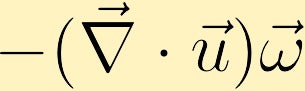
warstwy płynu o stałej gęstości (izopiknale) chcą pokrywać się z warstwami o stałym ciśnieniu (izobary). Jeśli te warstwy nie pokrywają się, płyn zaczyna się obracać, aby je wyrównać, co powoduje generowanie wirowości. (W przykładzie zaczynamy od zera.)

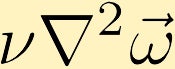
siły lepkie powodują dyfuzję wiru. (W przykładzie zaczynamy od punktu nieskończonej wirowości w centrum.)