A Revolucionária Teoria de Galois

Em 31 de Maio de 1832, um francês Republicano revolucionário chamado de Évariste Galois morreu de um tiro. Ele tinha 20 anos. Na noite anterior, temendo sua própria morte, Galois escreveu muitas cartas, rabiscando freneticamente “Não tenho tempo; Não tenho tempo”. Uma carta é particularmente preciosa por razões históricas. Nesta carta, Galois afirma ter realmente desencadeado a revolução. Não é política. Mas matemática.tinha?A revolução iniciada por Galois acabou por ser maior e mais profunda do que ele poderia imaginar! A paisagem da matemática tem sido profundamente afetada pela visão de Galois, à medida que a sua descendência subiu e assumiu o mundo matemático. Esta progênie é agora onipresente e governa terras sem limites. Vai sob o nome de pura álgebra.para romantizar um pouco mais a história da vida dramática de Galois, aqui está um resumo de um documentário que fiz sobre álgebra:

ele definitivamente é! Mas a sua revolução matemática não correu bem. Como todo líder da revolução, ele primeiro teve as maiores dificuldades. Não para imaginar a revolução. Mas para convencer os outros a juntarem-se a ele numa abordagem de mudança de jogo da matemática. Quando Galois ainda estava vivo, as suas ideias revolucionárias foram rejeitadas várias vezes pela Academia francesa de Ciências… porque os melhores matemáticos Franceses daquela época, como Siméon Denis Poisson, simplesmente não conseguiram! Em parte devido à letra ilegível de Galois exibida à direita … como é que a teoria de Galois ainda era conhecida?em 1843, 10 anos após a morte de Galois, finalmente, um brilhante matemático francês chamado Joseph Liouville conseguiu captar algumas das ideias de Galois. Depois de mais 3 anos de trabalho, Liouville publicou um artigo para explicá-los. Mas o artigo de Liouville ainda era demasiado rebuscado para outros matemáticos apreciarem e compreenderem. Levou mais 24 anos para encontrar um matemático francês notável o suficiente para entender melhor Galois e tornar suas ideias límpidas. Este matemático notável é Camille Jordan. Na Verdade, O Livro de Jordan de 1870 sobre a teoria de Galois foi tão bem escrito que o matemático alemão Felix Klein achou-o tão legível como um livro alemão!Haha! Acho que isto realmente desencadeou a Revolução de Galois!foi definitivamente um grande impulso. Mas seriam precisos mais 82 anos para o grande matemático austríaco Emil Artin finalmente dar à teoria de Galois a sua forma moderna, em 1942. O Artin merece muitos créditos. Enquanto Galois foi o visionário que previu esta revolução, Artin, em muitos sentidos, é o que realmente empreendeu a revolução e derrubou a matemática. Graças a Artin, e a alguns outros, Hoje, a teoria de Galois tornou-se uma pedra angular inevitável da pesquisa em matemática, com muitas conquistas surpreendentes e surpreendentes (como a prova de Wiles do último teorema de Fermat), bem como um enorme reservatório de perguntas e mistérios abertos!este artigo vai empurrá-lo cada vez mais intelectualmente. O conhecimento de álgebra linear, números complexos e teoria dos grupos pode ser útil para uma leitura mais fácil das seções 2, 4 e 5, respectivamente. Mas, seja corajoso, como a recompensa é ter uma boa visão geral de uma das mais belas e perspicazes teorias da matemática!
Fields in Pure Algebra
Galois theory is about symmetries of numbers. Mas antes de chegar lá, tenho de te apresentar para te armar, revelando-te um segredo sobre números. E tenho a certeza que já ouviste falar! Na verdade, no ensino médio, você provavelmente foi ensinado a nunca deixar raízes nos denominadores.o que queres dizer?
quero dizer que $1 / (\sqrt{2}-1)$ não foi uma resposta certa. Pode ajudar a livrar-se da raiz quadrada de 2 no denominador?sim! Isto faz-me lembrar algo… mas não me lembro do que era suposto fazermos…
Hehe… ensinaram-nos a multiplicar-nos para cima e para baixo pelo conjugado do denominador. Este conjugado é obtido substituindo $-$ por $+$ (ou vice-versa) no denominador:
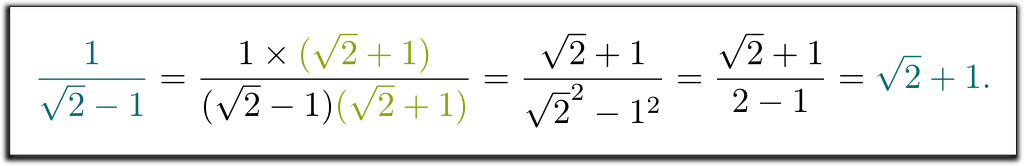
mas e $1 / (\sqrt{2}-1)$? Podes livrar-te da raiz no denominador? Pode ser feito?
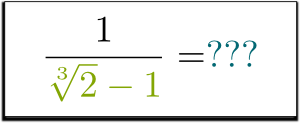
Hehe… curiosamente, qualquer poder de $\sqrt{2}-1$ pode ser escrito como uma soma de poderes de $\sqrt{2}$. Na verdade, você só precisa distribuir os produtos:
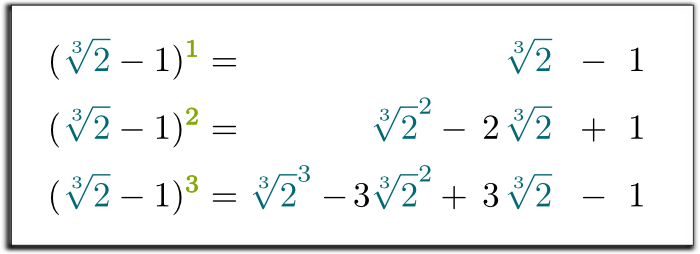
então agora temos 3 equações, com 2 expressões raiz que queremos livrar-nos! Assim, podemos combinar as equações para remover todas as expressões de raiz à direita!Hummm … como?
Vamos multiplicar as 2 primeiras linhas por 3 e somar os 3 equações:
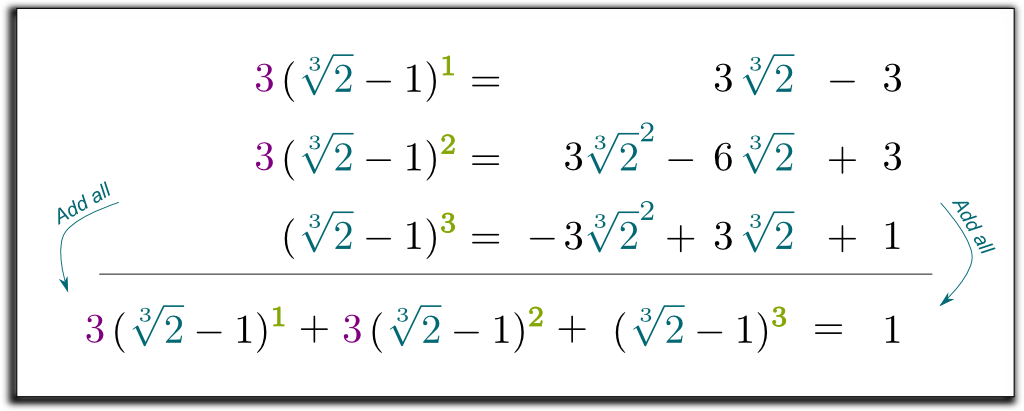
Hehe … a coisa legal é que o termo esquerdo que obtivemos agora pode ser factorizado por $\sqrt{2}-1$! Deixe-me saltar alguns cálculos aborrecidos… e chegar ao resultado $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Então, para nos livrarmos das raízes no denominador, podemos multiplicar para cima e para baixo por $\sqrt{2}^2 + \sqrt{2} + 1$! Finalmente, temos a seguinte fórmula surpreendente e bela:
Agora, o que era de particular interesse para Galois não era o fato de que um método habilitado para remover radicais de denominadores. Mas em vez disso, qualquer número com radicais em denominadores igualou um número com radicais no topo. Isto significava que os números com radicais no topo eram estáveis por divisão.o que queres dizer?
é comum denotar $\mathbb Q{2}]$ o conjunto de números que podem ser escritos como uma soma de poderes de $\sqrt{2}$. Uma vez que $\sqrt{2}^3 = 2$ é um número racional, qualquer soma de poderes de $\sqrt{2}$ pode de facto ser escrita no formulário padrão $a\sqrt{2}^2 + b\sqrt{2} + c$. Agora, se você adicionar, subtrair ou multiplicar quaisquer dois desses números, então não é difícil ver que obtemos números que ainda podem ser colocados no formulário padrão $a\sqrt{2}^2 + b\sqrt{2} + c$. Além disso, o que acabamos de mostrar aqui é que o inverso de todos os números $a\sqrt{2}^2 + b\sqrt{2} + C$ também pode ser escrito em forma padrão. Isso mostra que qualquer adição, subtração, multiplicação e divisão de números em $\mathbb Q{2}]$ produz um número, que pode ser escrita na forma padrão… e, portanto, pertence a $\mathbb Q{2}]$. Em termos de álgebra pura, $\mathbb Q{2}]$ é assim estável pelas quatro operações aritméticas clássicas. Por esta razão, chamamos-lhe Campo.
geometria das extensões de Campos
o campo com o qual está mais familiarizado é provavelmente o conjunto $\mathbb Q$ dos números racionais. Outros exemplos de campos são os conjuntos $\mathbb R$ de números reais e o conjunto $\mathbb C$ de números complexos. E agora, também temos $ \mathbb Q{2}$. Dado que $\mathbb Q{2}]$ é um campo que contém o campo $\mathbb Q$, dizemos que $\mathbb Q{2}] / \mathbb Q$ é uma extensão de campo.
o fato de que $\mathbb Q{2}] / \mathbb Q$ é uma extensão de campo produz uma conexão muito natural entre os dois campos. Ou seja, $\mathbb Q{2}]$ pode ser visto como um espaço vetorial, onde $\mathbb Q$ é o campo escalar. Em particular, o fato de que qualquer número, em $\mathbb Q{2}]$ pode ser escrito $\sqrt{2}^2 + b\sqrt{2} + c$ significa que $(1, \sqrt{2}, \sqrt{2}^2)$ formulários de uma base de us $\mathbb Q{2}]}$ em $\mathbb Q$-espaço vetorial. E isso significa que podemos representá-lo geometricamente como um espaço de 3 dimensões!
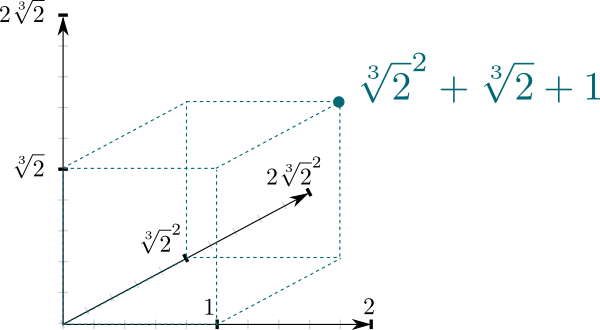
a dimensão do espaço vetorial acima é uma propriedade interessante de extensões de campo. É conhecido como o grau, e é comumente denotado $\big{2}] : \mathbb Q\big] = 3$ por exemplo.
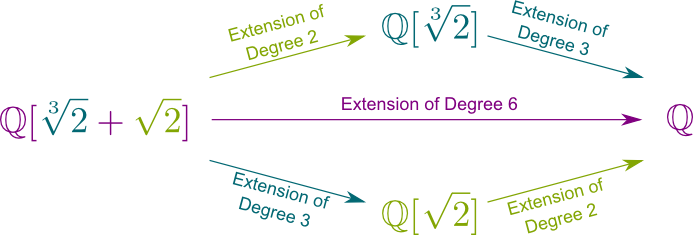
mais genericamente, qualquer extensão de campo finita de $\mathbb Q$ Pode ser escrita $\mathbb Q$ com algum $x$ que é adicionado a $\mathbb Q$.os graus das extensões de campo podem ser infinitos?Sim. É o caso da extensão de campo $\mathbb R/ \ mathbb Q$. E, assim é a extensão de campo mais importante na teoria de Galois! Esta extensão de campo é $\bar {\mathbb Q} / \mathbb Q$, Onde $\bar{\mathbb Q}$ é o conjunto de números algébricos. Estas são todas as soluções para equações polinomiais da forma $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. Por exemplo, $\sqrt{2}$ é um número algébrico porque é solução para $x^4 – 2x = 0$. Assim, $\bar {\mathbb Q}$ é uma extensão de campo para todas as extensões de campo finitas de $\mathbb Q$.
números conjugados
estamos quase lá! Precisamos de um desvio final através de equações polinomiais.

exatamente! Estas são conhecidas como equações polinomiais irredutíveis. A equação $x^3-2 = 0$ é um exemplo de equação polinomial irredutível.
vamos considerar $x^2 – 2x -1=0$ para ter algumas pistas. Esta equação pode ser provada como irredutível. Lembras-te como resolvê-lo?
Se $ B^2-4ac \ geq 0$, Sim.
A primeira coisa a notar é que, se $x_1$, $x_2$, …, $x_n$ são todas as soluções de um polinômio irredutível de equação $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$, com coeficientes racionais, então este polinômio irredutível equação, na verdade, pode ser reescrito $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. A identificação dos termos constantes produz então $x_1 x_2 … x_n $ = $ (-1)^n a_0/a_n$. Então, crucialmente, o produto dos números conjugados é o número racional $(-1)^n a_0/a_n$, que é não-zero (prove-o!).
Aqui está uma pequena piada para ter em mente a forte ligação entre conjugados:

considere uma fração $1 / x_ 1$, onde $x_ 1$ é uma expressão complicada com radicais. Multiplicando para cima e para baixo pelos conjugados $x_2$, …, $x_n$ de $x_1$ então rende $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, o que não tem nenhum radical no denominador porque estabelecemos $a_0$ como sendo um número não-zero do campo de base!Waw! Da hora! E que tal $ \sqrt{2}$? Quais são os seus conjugados?
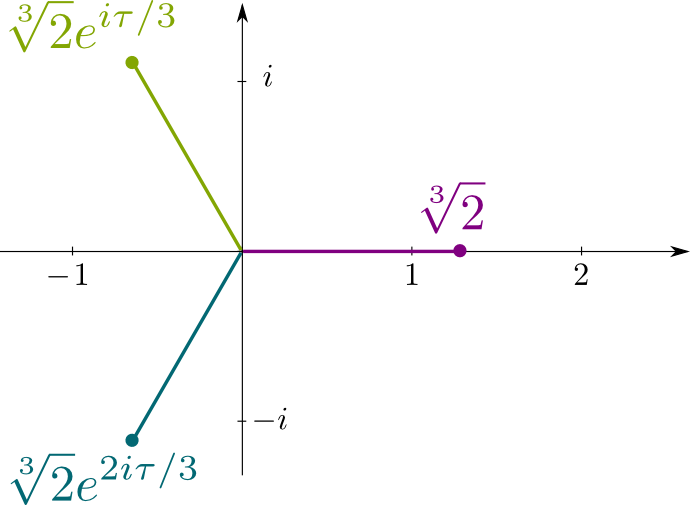
Recall that $x^3-2=0$ is the irreducible polynomial equation $\sqrt{2}$ is the solution of. Assim, conjuga são as outras soluções para essa equação, que são os números complexos $\sqrt{2}j$ e $\sqrt{2}j^2$, onde $j= e^{i\tau/3}$ com $\tau = 2\pi$, sendo o rácio entre a circunferência de um círculo através de seu raio. A figura seguinte mostra as localizações das soluções conjugadas neste plano complexo:
ambiguidade de Galois
finalmente, estamos a chegar à visão chave de Galois!o que é?os conjugados
são perfeitamente permutáveis. Isto significa que, se você alterar sistematicamente $\sqrt{2}$ pelo seu conjugado $-\sqrt{2}$, então as igualidades ainda se mantêm. Por exemplo, uma vez que tínhamos $1/(\sqrt{2}-1) = \sqrt{2}+1$, posso dizer-lhe directamente que $1/(- \sqrt{2}-1)= – \sqrt{2}+1$! Similarmente, temos a seguinte implicação impressionante:
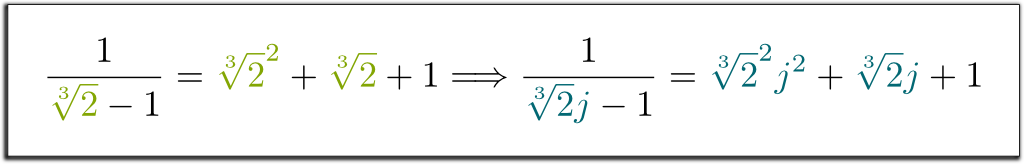
Hehe… deixe-me recordar primeiro que os campos finitos são percorridos por um único elemento. Então, se o campo base for $\mathbb Q$, qualquer campo finito pode ser escrito $\mathbb Q$ para algum $x_1$. Agora, considere $x^n + a_{n-1}x^{n-1} $ + $ … + a_1 x + a_0 = 0$ a equação polinomial irredutível $x_1$ é a solução de. Então, o que define a $\mathbb P$ é $\mathbb Q$-espaço vetorial gerado por $x_1$, $x_1^2$, …, $x_1^{n-1}$, com a simplificação dos maiores poderes de us $x_1$ de acordo com a regra algébrica $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.
de uma forma muito semelhante (mas mais forte) que dois espaços vetoriais de dimensão 2 são mais ou menos iguais! Isto tem uma terrível consequência. Significa que, de uma perspectiva algébrica, não faz sentido fazer a diferença entre um número e qualquer um dos seus conjugados (desde que você sistematicamente substitua o número pelo seu conjugado)! Então, por exemplo, $\sqrt{2}$ e $-\sqrt{2}$ são algebricamente indistinguíveis! Para ter isso em mente, aqui está outra piada que eu inventei:

Galois particularmente focados em extensões de campo que são estáveis por conjugação. Tais extensões de campo estáveis são agora conhecidas como extensões Galois. Então, se $x_1 $ pertence a uma extensão Galois, então esta extensão Galois contém todos os seus conjugados $x_2$,…, $x_n$.
a simple way to construct Galois extensions consists in taking the field spanned by solutions of an irreducible polynomial equation. Por exemplo, se $x_ 1$,…, $x_n$ são conjugados para o campo base $\mathbb Q$, então $\mathbb Q / \mathbb Q$ é uma extensão Galois. Os campos construídos desta forma são chamados campos de divisão.
por exemplo, o campo de repartição da equação $x^3-2=0$ é a extensão Galois $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ estendida pelas suas soluções.o que há de tão interessante nas extensões Galois?
Se $x_1$ abrange uma extensão Galois, então o mesmo acontece com os seus conjugados. Assim, $\mathbb Q = \mathbb Q = $ … $ = \mathbb Q$ = $\mathbb Q$. Assim, o isomorfismo entre $\mathbb Q$ e $\mathbb Q$ Que consiste em sempre substituir $x_1$ por $x_2$ é de fato um isomorfismo entre $\mathbb Q$ e ele mesmo! Chamamos-lhe automorfismo. Automorphisms of a Galois extension $\mathbb Q / \mathbb Q$ forms the Galois group $Gal (\mathbb Q/\mathbb Q)$.
agora, crucialmente, se $\mathbb Q = \mathbb Q$, então todos os automorfismos de uma extensão Galois $\mathbb Q / \mathbb Q$ são permutações de $x_1$ com um de seus conjugados! Em particular, vemos aqui que a cardinalidade de um grupo Galois é igual ao grau da extensão Galois.pode dar um exemplo?claro! Você pode notar que $\mathbb Q = \mathbb Q$ e $\mathbb Q = \mathbb Q$, O que significa que $i$ e $\sqrt{2}$ cada abrange os campos de divisão da equação polinomial irredutível de que são solução. Assim, $\mathbb Q / \mathbb Q$ e $\mathbb Q/\mathbb Q$ são ambas extensões Galois. Portanto, seus automorfismos consistem em substituir $ i$ por um de seus conjugados, $i$ ou $ – i$, e substituir $\sqrt{2} $ por $\sqrt{2}$ ou $ – \sqrt{2}$. Nos primeiros casos, não estamos mudando nada para números, o que corresponde à simetria zero. Os segundos casos podem ser visualizados como simetrias axiais, como mostrado na figura abaixo:

não é incrível?é bom… mas podemos ter simetrias mais complicadas?claro! Vamos para o campo de divisão $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2]$ de $x^3-2=0$. Mas, antes de ir mais longe, vamos notar que $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.como provamos a igualdade?só precisamos de provar que todos os geradores de um campo pertencem ao outro. Vamos começar por provar que os geradores do último, $\sqrt{2}$ e $j$, pertencem ao primeiro. É óbvio por $ \sqrt{2}$. Agora, $j = (\sqrt{2} j) / \sqrt{2}$, portanto $j$ pertencem ao campo anterior também. Isto prova que todos os elementos de $ \mathbb Q{2}, j]$ pertencem a $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Reciprocamente, é simples que todos os geradores do campo anterior, $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$, são produtos dos geradores do último. Assim, ambos os campos são iguais. E, em particular, $\mathbb Q{2}, j] / \mathbb Q$ é uma extensão Galois.fixe! Então, o que é o Grupo Galois $Gal (\mathbb Q{2}, j]/\mathbb Q)$?
Hehe … para entender as simetrias de $\mathbb Q{2}]$, Vamos precisar ir mais longe no estudo de Galois de grupos Galois …
correspondência Galois
o problema com grupos Galois é que eles podem se tornar extremamente grandes e complicados. Este é particularmente o caso do grupo infinito $Gal (\bar{\mathbb Q}/\mathbb Q)$. Para apreender grupos tão grandes e complexos, Galois teve a brilhante ideia de quebrá-los em pedaços menores.como podemos quebrar os grupos Galois?
surpreendentemente, Galois descobriu que os grupos Galois poderiam ser divididos em subgrupos de simetrias apenas olhando para aqueles que deixam algum subcampo inalterado. Por exemplo, $\mathbb Q$ é um subcampo de $\mathbb Q{2}, j]$, uma vez que qualquer número do primeiro pertence ao segundo. Assim, simetrias de $\mathbb Q{2}, j]$ que não mudam nada para $\mathbb Q$ formam um subgrupo do Grupo Galois de $\mathbb Q{2}, j]/\mathbb Q$. Estas simetrias formam o Grupo Galois $Gal (\mathbb Q{2},j]/\mathbb Q)$.Uau! Isto está a ficar abstracto!eu sei! Gosto de visualizar estas simetrias como as formas de ligar $\mathbb Q{2},j]$ em $\mathbb Q$. Aqui está uma imagem imaginada do “ligar”:
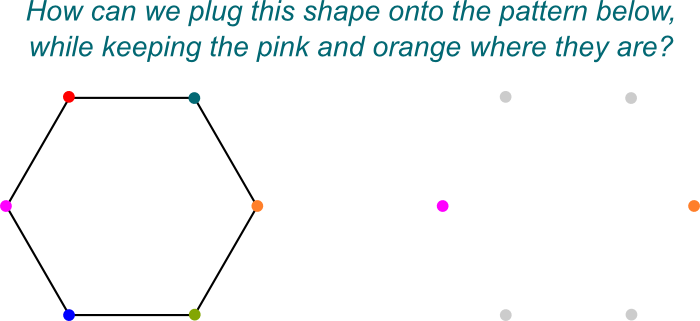

em vez de tentar descrever este grupo directamente, vamos concentrar-nos no seu subgrupo $Gal(\mathbb Q{2}, j]/\mathbb Q)$. É simples que $\sqrt{2}$ spans $\mathbb Q{2}, j]$ quando adicionado a $\mathbb Q$. Assim, $\mathbb Q{2}, j] / \mathbb Q$ é uma extensão Galois estendida por $\sqrt{2}$. Portanto, usando um teorema que vimos anteriormente, sabemos que todos os automorfismos desta extensão Galois consistem em substituir $\sqrt{2}$ por um dos seus 3 conjugados (em si, $\sqrt{2} j$ e $\sqrt{2} j^2$)!
Agora, eu poderia continuar a estudar outras peças de $Gal(\mathbb Q{2}, j]/\mathbb Q)$, como o Galois subgrupo $Gal(\mathbb Q{2},j]/\mathbb Q{2}])$. Mas prefiro usar outro dos poderosos teoremas de Galois. Ou seja, ele provou que se $\mathbb Q/\mathbb Q$ foi, além disso, uma extensão Galois em si, então o subgrupo $Gal(\mathbb Q{2}, j]/\mathbb Q)$ é normal.
assim, o Grupo Galois de $\mathbb Q{2},j]/\mathbb Q$ Pode ser quociado por este subgrupo, e o grupo quociente então é igual a $Gal (\mathbb Q/\mathbb Q)$. No entanto, $\mathbb Q / \ mathbb Q$ é de facto uma extensão Galois estendida por $j$, cujo conjugado é $j^2$. Assim, $Gal (\mathbb Q/\mathbb Q)$ consiste em deixar $j$ como $j$ ou substituí-lo por $j^2$.
podemos agora deduzir todas as simetrias de $Gal(\mathbb Q{2},j]/\mathbb Q)$ combinando estas de $Gal (\mathbb Q{2},j] / \mathbb Q)$ e $Gal (\mathbb Q/\mathbb Q)$. Podemos apresentar estas simetrias pelo desenho como eles afetam nossas três abrangendo conjuga $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$:
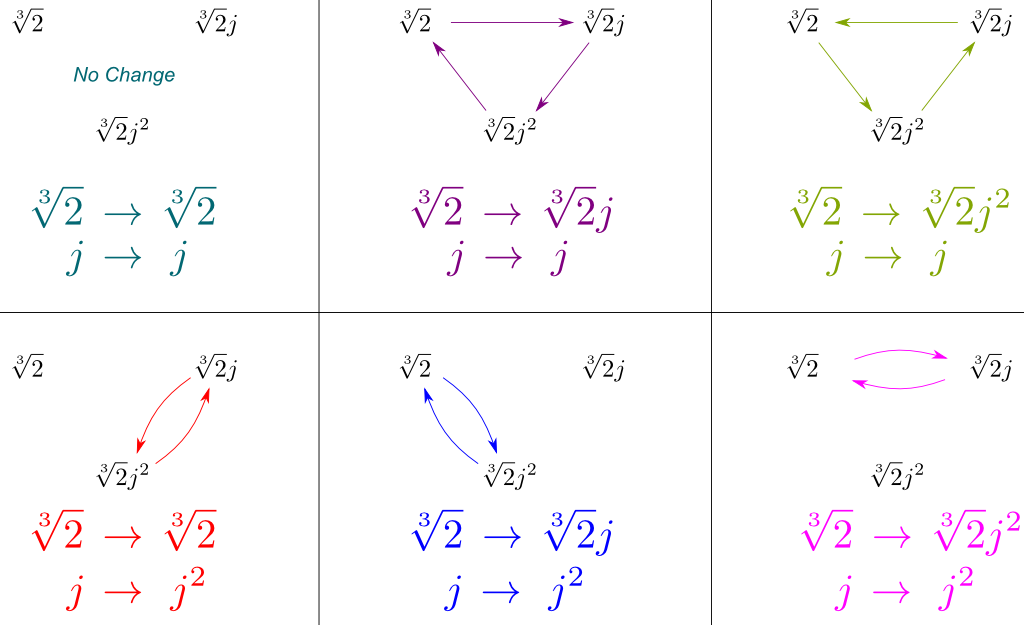
crucialmente, a figura acima contém todas as simetrias de $Gal (\mathbb Q{2}, j] / \mathbb Q)$. E surpreendentemente, estas simetrias correspondem a um conhecido grupo de simetria.qual é o conhecido grupo de simetria?vou deixar o Marcus du Sautoy apresentá – lo.:então, as simetrias aqui são como uma estrela-do-mar ou como um triângulo?como um triângulo, obviamente!sim, de facto! Este grupo de simetrias do triângulo é chamado $D_3$, e é o mesmo que o grupo $S_3$ de permutações de 3 elementos. Isto nos leva à seguinte fórmula, que eu achei tão bonita, que eu decidi moldá-la!
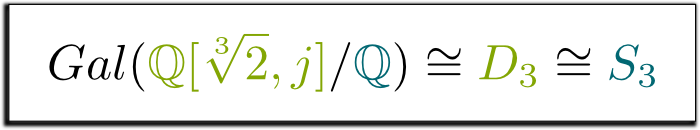
Let’s Conclusion
In many ways, Galois is to be regarded as the father of modern algebra. Sua visão fundamental era olhar para a matemática através do ângulo das regras de operações, e isso o levou a revelar ambiguidades surpreendentes e perspicazes, ou simetrias, entre números. De uma perspectiva algébrica, números como $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$ são perfeitamente simétricos e totalmente intercambiáveis.mas, a teoria de Galois tem alguma aplicação?
a compreensão destas simetrias tem tido aplicações surpreendentes na geometria algébrica e topologia algébrica, entre outras. In particular, early successes of the theory include a classification of constructible regular polygons and a theorem asserting that high degree polynomial equations could not be solved by radicals.
recent successes appear in cryptography and Andrew Wiles’ proof of Fermat’s last theorem. Esta prova envolve estudar o Grupo Galois $Gal (\bar{\mathbb Q} /\mathbb Q)$ com representação de grupo. Mas eu diria que a teoria ainda é jovem, e muito resta para descobrir. Afinal de contas, é uma das áreas de pesquisa mais ativas na pesquisa de matemática pura de hoje.isto deve levar-nos a pagar muito mais tributos ao incrível génio de Galois… deixem-me incluir um por SocraticaStudios.