Fronteiras em Genética
Introdução
tamanho Efetivo populacional (Ne) é um importante genético parâmetro que estima a quantidade de deriva genética em uma população, e tem sido descrito como o tamanho de uma idealizada de Wright–Fisher população esperado para produzir o mesmo valor de um dado parâmetro genético como na população em estudo (Crow e Kimura, 1970). Os tamanhos Ne podem ser influenciados por flutuações no tamanho da população recenseada (Nc), pela relação entre o sexo reprodutivo e a variância no sucesso reprodutivo.a estimativa pode ser obtida utilizando abordagens que se enquadram em três categorias metodológicas: demográficas, baseadas em pedigree ou baseadas em Marcadores (Flury et al., 2010). Os dados genealógicos têm sido tradicionalmente utilizados para obter estimativas Ne em animais. No entanto, estimativas confiáveis de Ne dependem do pedigree estar completo. Este estado de conhecimento é viável em algumas populações domésticas, cujos parâmetros demográficos foram rigorosamente controlados por um número suficientemente grande de gerações. No entanto, na prática, a aplicabilidade desta abordagem continua limitada a alguns casos que envolvem raças altamente geridas (Flury et al., 2010; Uimari e Tapio, 2011).
uma solução para superar a limitação de uma pedigree incompleta é estimar a tendência recente em Ne usando dados genômicos. Vários autores reconheceram que Ne poderia ser estimado a partir de informações sobre desequilíbrio de articulação (ld) (Sved, 1971).; Hill, 1981). LD descreve a associação não-aleatória de alelos em diferentes loci como uma função da taxa de recombinação entre as posições físicas do loci no genoma. No entanto, LD assinaturas também podem resultar de processos demográficos, tais como mistura e deriva genética (Wright, 1943; Wang, 2005), ou através de processos como a “carona” durante a seletiva varre (Smith e Haigh, 1974) ou seleção de plano de fundo (Charlesworth et al., 1997). Em tais cenários, alelos em diferentes loci tornam-se associados independentemente da sua proximidade no genoma. Assumindo que uma população é fechada e panmática, o valor LD calculado entre loci neutro não ligado depende exclusivamente da deriva genética (Sved, 1971; Hill, 1981). Esta ocorrência pode ser usada para prever Ne devido à relação conhecida entre a variância em LD (calculada usando frequências alelas) e o tamanho efectivo da população (Hill, 1981).recentes avanços na tecnologia de genotipagem (e.g., usando matrizes de contas SNP com dezenas de milhares de sondas de DNA) permitiram a coleta de grandes quantidades de dados de ligação em todo o genoma, ideais para estimar o Ne em animais e seres humanos, entre outros (por exemplo, Tenesa et al., 2007; De Roos et al., 2008; Corbin et al., 2010; Uimari e Tapio, 2011; Kijas et al., 2012). No entanto, uma ferramenta de software que permite a estimativa de Ne a partir de LD está faltando, e pesquisadores atualmente dependem de uma combinação de ferramentas para manipular dados, inferir LD, e tendem a usar scripts sob medida para realizar os cálculos apropriados e estimar Ne.
Aqui nós descrevemos o SNeP, uma ferramenta de software que permite a estimativa das tendências Ne através da geração usando dados SNP que corrige para o tamanho da amostra, faseamento e taxa de recombinação.
materiais e métodos
o método que SNeP utiliza para calcular LD depende da disponibilidade de dados em fase. Quando a fase é conhecida, o usuário pode selecionar o coeficiente de correlação de Hill e Robertson (1968) ao quadrado que faz uso de frequências haplotype para definir LD entre cada par de loci (equação 1). No entanto, na ausência de uma fase conhecida, o coeficiente de correlação produto-momento de Pearson quadrado entre pares de loci pode ser selecionado. Embora estas duas abordagens não sejam as mesmas, são altamente comparáveis (McEvoy et al., 2011):
onde pA e pB são, respectivamente, as freqüências dos alelos A e B em duas diferentes loci (X, Y), medido para n indivíduos, pAB é a frequência do haplótipo com alelos a e B na população estudada, X e Y são a média do genótipo de frequências para o primeiro e segundo lugar, respectivamente, Xi é o genótipo do indivíduo i no primeiro locus e Yi é o genótipo do indivíduo i no segundo locus. A equação (2) correlaciona as contagens de alelos genotípicos em vez das frequências de haplotipos e não é influenciada por heterozigotos duplos (esta abordagem resulta nas mesmas estimativas que a opção –r2 em PLINK).
SNeP estimativas histórica tamanho efectivo da população, com base na relação entre r2, Ne, e c (taxa de recombinação), (Equação 3—Sved, 1971), e permitindo que os usuários incluem correções para o tamanho da amostra e a incerteza do gametic fase (Equação 4—Weir e Hill, 1980):
, onde n é o número de indivíduos amostrados, β = 2, quando a gametic fase é conhecida e β = 1, se, em vez disso, a fase não é conhecido.
várias aproximações são usadas para inferir a taxa de recombinação usando a distância física (δ) entre dois loci como referência e traduzindo-a em distância de ligação (d), que é geralmente descrita como Mb(δ) ≈ cM(d). Para valores pequenos de d a última aproximação é válida, mas para valores maiores de d a probabilidade de vários fenómenos de recombinação e interferência aumenta, além disso, a relação entre a distância do mapa e da taxa de recombinação não é linear, como a máxima taxa de recombinação possível é de 0,5. Thus, unless using very short δ, the approximation D ≈ c is not ideal (Corbin et al., 2012). Assim, implementamos funções de mapeamento para traduzir o d estimado em c, seguindo Haldane (1919), Kosambi (1943), Sved (1971), e Sved e Feldman (1973). Initially SNeP infers d for each pair of SNPs as directly proportional to δ according to D = kδ where k is a user defined recombination rate value (default value is 10-8 as in Mb = cM). O valor inferido de δ pode então ser submetido a uma das funções de mapeamento disponíveis, se exigido pelo utilizador.
equação de Resolução (3) para Ne e incluindo todas as correções descritas, permite a previsão de Ne a partir de dados LD usando (Corbin et al., 2012):
em que Nt é o tamanho efectivo da população t há gerações calculado como t = (2f(ct)) -1 (Hayes et al., 2003), a tc é a taxa de recombinação definidos para uma determinada distância física entre os marcadores e, opcionalmente, ajustado com o mapeamento de funções mencionadas acima, r2adj é o LD valor ajustado para o tamanho da amostra e α:= {1, 2, 2.2} é uma correção para a ocorrência de mutações (Ohta e Kimura, 1971). Portanto, LD sobre distâncias recombinantes maiores é informativo em Ne RECENTE, enquanto distâncias mais curtas fornecem informações sobre tempos mais distantes no passado. Um sistema de binning é implementado a fim de obter valores R2 médios que refletem LD para distâncias inter-locus específicas. O sistema de binning implementado usa a seguinte fórmula para definir os valores mínimo e máximo para cada bin:
Onde bi (ℕ1) é a i-ésima bin do número total de bins (totBins), mente, e maxD são, respectivamente, o mínimo e o máximo da distância entre SNPs e x é um número real positivo (ℝ0) Quando x é igual a 1, a distribuição das distâncias entre as posições é linear e cada lixeira possui a mesma faixa de distância. Para valores maiores de x, a distribuição das distâncias muda permitindo uma gama maior nos últimos contentores e uma gama menor nos primeiros contentores. Variando este parâmetro permite ao usuário ter um número suficiente de comparações emparelhadas para contribuir para a estimativa Ne final para cada barra.
aplicação de exemplo
testamos SNeP com dois conjuntos de dados publicados que tinham sido usados anteriormente para descrever tendências em Ne ao longo do tempo usando LD, Bos indicus e Ovis aries . As estimativas de R2 para os conjuntos de dados de gado foram obtidas pelos autores usando GenABLE (Aulchenko et al., 2007) using a minimum allele frequency (MAF) < 0,01 and adjusting the recombination rate using Haldane’s mapping function (Haldane, 1919). As estimativas de R2 dos dados sobre ovelhas foram calculadas pelos autores usando PLINK-1.07 (Purcell et al., 2007), with a MAF < 0,05 and no further corrections. Para ambos os conjuntos de dados autossómicos, o r2 estima, quando corrigido para a dimensão da amostra utilizando a equação (4) Com β = 2. Para estas análises comparativas, a linha de comando SNeP incluiu os mesmos parâmetros utilizados para os dados publicados, além das estimativas r2, calculadas através da contagem de genótipos e do uso da nova estratégia de binning da SNeP.
resultados
SNeP é uma aplicação multithreaded desenvolvida em C++ e binários para os sistemas operacionais mais comuns (Windows, OSX e Linux) podem ser baixados dehttps://sourceforge.net/projects/snepnetrends/. Os binários são acompanhados por um manual que descreve o uso Passo-a-passo de SNeP para inferir tendências em Ne como descrito aqui. SNeP produz um arquivo de saída com tabulação delimitada colunas mostrando o seguinte para cada bin que foi usado para estimar Ne: o número de gerações no passado a que o bin corresponde (e.g., 50 gerações atrás), a estimativa Ne correspondente, a distância média entre cada par de SNPs no bin, a média r2 e o desvio padrão de r2 no bin, e o número de SNPs usados para calcular r2 no bin. Este arquivo pode ser facilmente importado no Microsoft Excel, R ou outro software para traçar os resultados. Os gráficos aqui apresentados (Figuras 1, 3) correspondem às colunas de gerações atrás e Ne do ficheiro de saída. A coluna com o desvio-padrão r2 é fornecida para que os utilizadores inspecionem a variância na estimativa Ne em cada cesto, especialmente para as caixas que refletem estimativas de tempo mais antigas e que são menos fiáveis à medida que o número de PNS utilizados para estimar r2 se torna menor.
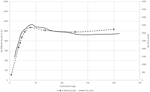
a Figura 1. Comparação das tendências Ne de seis raças suíças de ovinos de acordo com Burren et al. (2014) (linhas tracejadas) e este trabalho (linhas sólidas).
o formato necessário para os ficheiros de entrada é o formato PLINK padrão (ficheiros ped e mapas) (Purcell et al., 2007). O SNeP permite que os usuários calculem LD nos dados descritos acima, ou usem uma matriz ld pré-calculada personalizada para estimar Ne usando a equação (5).
A interface de software permite ao usuário controlar todos os parâmetros da análise, por exemplo, a distância entre SNPs na bp, e o conjunto de cromossomos utilizados na análise (por exemplo, 20-23). Além disso, o SNeP inclui a opção de escolher um limiar MAF (padrão 0.5), uma vez que foi demonstrado que a contabilização da MAF resulta em estimativas R2 não distorcidas, independentemente da dimensão da amostra (Sved et al., 2008). SNeP da arquitetura de vários segmentos permite um rápido cálculo de grandes conjuntos de dados (nós testamos até ~100 K SNPs para um único cromossomo), por exemplo, o BOS dados aqui descritos foram analisados com um processador de 2’43”, o uso de dois processadores reduziu o tempo de 1’43”, quatro processadores reduziu o tempo de análise para 1’05”.
Zebu Exemplo
Para o zebu análise, as formas de Ne curvas obtidas com o SNeP e seus dados publicados tendências mostrou a mesma trajetória com um suave declínio, até cerca de 150 gerações atrás, seguido por uma expansão com um pico em torno de 40 gerações atrás e terminando em um acentuado declínio nas gerações mais recentes (Figura 1). No entanto, enquanto as tendências em ambas as curvas eram as mesmas, as duas abordagens resultaram em diferentes estimativas Ne, com os valores da SNeP sendo aproximadamente três vezes maiores do que os do papel original. Enquanto tentávamos usar os parâmetros dos autores em nossas análises, algumas diferenças eram inevitáveis, ou seja, a publicação original dos dados do gado estimado r2 com uma abordagem diferente da implementada no SNeP. As análises com SNeP foram baseadas em genótipos, enquanto a análise original foi baseada em dois haplotipos locus inferidos, o que resulta nos dados publicados mostrando um R2 esperado de 0.32 à distância mínima, enquanto nossas estimativas foram 0.23. Similarmente, Mbole-Kariuki et al. (2014) obteve um nível de fundo r2 = 0,013 em torno de 2 Mb, enquanto nossa estimativa na mesma distância foi 0.0035 (dados não apresentados). Consequentemente, como nossas estimativas de LD eram consistentemente menores que Mbole-Kariuki et al. (2014) espera-se que as nossas estimativas Ne sejam maiores. Embora esta observação sublinhe a importância de uma escolha cuidadosa dos parâmetros e dos seus limiares, é importante salientar que, embora a magnitude absoluta dos valores Ne seja diferente, as tendências são quase idênticas.as seis raças suíças de ovinos analisadas com o SNeP produziram resultados comparáveis aos do papel original (Figura 2), com curvas de tendência Ne geralmente sobrepostas (Figura 3). No entanto, a tendência geral em Ne mostrou um declínio para o presente. SNeP produziu valores ligeiramente maiores de Ne para o passado mais distante (700-800 gerações). Isto é devido ao sistema binning diferente usado em SNeP, que permite ao usuário obter uma distribuição mais uniforme de comparações emparelhadas dentro de cada bin (i.e., o número de comparações emparelhadas SNP dentro de cada bin é comparável). Para o período de tempo que se estende para além de 400 gerações atrás, Burren et al. (2014) usado apenas três bandejas em sua análise, centrada no 400, 667, e 2000 gerações atrás), enquanto que no mesmo período de tempo SNeP usado 5 bandejas com um número de comparações em pares dependentes para o intervalo definido com fórmulas 6a,b. Consequentemente, Burren e colegas abordagem termina com uma maior densidade de dados, descrevendo as gerações mais recentes de descrever as mais antigas gerações. Portanto, o uso de menos latas tende a aumentar a presença de valores menores de Ne em cada caixa, consequentemente diminuindo o valor médio de Ne para cada caixa. Os valores Ne para o passado recente, comparados à 29ª geração no passado, deram resultados muito semelhantes. A maior diferença (50) foi obtida para a raça SBS.

Figura 2. Comparação entre os valores Ne recentes calculados na 29ª geração deste trabalho e Burren et al. (2014) para seis raças suíças de ovinos.
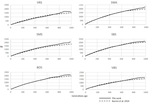
a Figura 3. Comparação das tendências Ne nas últimas 250 gerações nos dados da SHZ obtidos por Mbole-Kariuki et al. (2014) (linha tracejada) e usando SNeP (linha sólida).
discussão
a análise de Ne usando dados LD foi demonstrada pela primeira vez há 40 anos, e tem sido aplicada, desenvolvida e melhorada desde (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; De Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). O número tradicionalmente pequeno de SNPs analisados não é mais uma limitação, uma vez que os Chips SNP compreendem um número extremamente grande de SNPs, disponíveis em um curto espaço de tempo e a um preço razoável. Isto impulsionou o uso do método, que tem sido aplicado aos seres humanos (Tenesa et al., 2007; McEvoy et al., 2011), bem como para várias espécies domesticadas (Inglaterra et al., 2006; Uimari and Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Juntamente com estas melhorias, as limitações metodológicas tornaram-se evidentes e foram aqui abordadas, com a maioria dos esforços apontando para a correta estimativa da Ne recente. No entanto, o valor quantitativo da estimativa é altamente dependente do tamanho da amostra, o tipo de estimativa LD eo processo de binning (Waples e Do, 2008; Corbin et al., 2012), embora o seu padrão qualitativo dependa mais da informação genética do que da manipulação de dados.
até agora este método tem sido aplicado usando uma variedade de software, não existe uma abordagem padronizada para Binar os resultados e cada estudo tem aplicado uma abordagem mais ou menos arbitrária, por exemplo, binning para classes de geração no passado (Corbin et al., 2012), binning para classes de distância com uma gama constante para cada bin (Kijas et al., 2012) ou binning por classes de distância de uma forma linear, mas com caixotes maiores para os pontos de tempo mais recentes (Burren et al., 2014). Tanto quanto sabemos, o único software disponível que estima Ne através de LD é o NeEstimator (do et al., 2014), uma versão atualizada do antigo LDNE (Waples e Do, 2008) permitindo a análise de grande conjunto de dados (como 50k SNPChip). Importante é que, embora SNeP se concentre em estimar tendências históricas Ne, o objetivo do NeEstimator é produzir estimativas ne contemporâneas sem preconceitos, este último deve, portanto, ser considerado como uma ferramenta complementar ao investigar a demografia através de LD.
usámos o SNeP para analisar dois conjuntos de dados onde o método foi anteriormente aplicado. Os resultados obtidos para os dados relativos aos ovinos foram tanto quantitativa como qualitativamente comparáveis aos obtidos pela Burren et al. (2014), enquanto para os dados de Zebu obtivemos uma estimativa de tendência Ne que coincidia estreitamente com a de Mbole-Kariuki et al. (2014) although our point estimates of Ne were larger than those described for the data (Mbole-Kariuki et al., 2014). A discrepância entre estes dois resultados reflete que Burren e colegas produziram suas estimativas r2 usando PLINK (o software padrão para manipulação de dados SNP em larga escala) que usa a mesma abordagem usada para estimar R2 pela SNeP, enquanto Mbole-Kariuki et al. seguiu Hao et al. (2007) para a estimativa r2. O uso de diferentes estimativas para LD é fundamental para o aspecto quantitativo da Ne curva, onde, devido à hiperbólica correlação entre Ne e r2, uma diminuição no r2 em sua gama mais perto de 0 pode levar a uma grande mudança no Ne estimativas, enquanto que as diferenças nas estimativas são menos significativas quando o valor de r2 é elevado, isto é, mais perto de 1. Portanto, embora em um dos conjuntos de dados os valores Ne onde substancialmente diferentes, em ambos os casos as curvas Ne se sobrepuseram às originalmente publicadas.
Como já sugerido por outros autores, a fiabilidade das estimativas quantitativas obtidas com este método deve ser tomada com precaução, especialmente para os valores Ne relacionados com as gerações mais recentes e mais antigas (Corbin et al., 2012) porque para as gerações recentes, grandes valores de c estão envolvidos, não encaixando as implicações teóricas que Hayes propôs para estimar uma variável Ne ao longo do tempo (Hayes et al., 2003). Estimativas para as gerações mais antigas também podem não ser confiáveis como a teoria da coalescência mostra que nenhum SNP pode ser amostrado de forma confiável após 4NE gerações no passado (Corbin et al., 2012). Além disso, as estimativas Ne, e especialmente as relacionadas com gerações futuras no passado, são fortemente afetadas por fatores de manipulação de dados, tais como a escolha dos valores MAF e alfa. Além disso, a estratégia de binning aplicada pode interferir com a precisão geral do método, por exemplo, onde um número insuficiente de comparações emparelhadas são usadas para povoar cada bin.uma das aplicações do método é comparar demografias de raças. Neste caso, a forma das curvas Ne seria a ferramenta ideal para diferenciar diferentes histórias demográficas, mais do que seus valores numéricos, usando-as como uma potencial impressão digital demográfica para essa raça ou espécie, ainda tendo em consideração que a mutação, migração e seleção pode influenciar a estimativa Ne através de LD (Waples e Do, 2010). Além disso, uma cuidadosa consideração dos dados analisados com a SNeP (e outros softwares para estimar Ne) é muito importante, pois a presença de fatores de confusão, como a mistura, pode resultar em estimativas tendenciosas de Ne (Orozco-terWengel e Bruford, 2014).
O objetivo da SNeP é, portanto, fornecer uma ferramenta rápida e confiável para aplicar métodos LD para estimar Ne usando dados genotípicos de alta produção de uma forma mais consistente. Ele permite duas abordagens diferentes de estimativa r2 mais a opção de usar estimativas r2 a partir de software externo. O uso do SNeP não supera os limites do método e a teoria por trás dele, mas permite que o usuário aplique a teoria usando todas as correções sugeridas até à data.
contribuições do autor
MB concebeu e escreveu o software e o manuscrito. MB, MT e POtW testaram o software e realizaram as análises. MT, POtW, and MWB revised the manuscript. Todos os autores aprovaram o manuscrito final.
Declaração de conflito de interesses
os autores declaram que a investigação foi realizada na ausência de quaisquer relações comerciais ou financeiras que possam ser interpretadas como um potencial conflito de interesses.
agradecimentos
Agradecemos a Christine Flury por fornecer os dados sobre ovelhas e por discussões úteis. Agradecemos também aos dois revisores pelas sugestões úteis para melhorar este trabalho. MB foi apoiado pelo programa Master and Back (Regione Sardegna).Charlesworth, B., Nordborg, M., and Charlesworth, D. (1997). Os efeitos da seleção local, polimorfismo equilibrado e seleção de fundo sobre os padrões de equilíbrio da diversidade genética em populações subdivididas. Genet. Res. 70, 155-174. doi: 10.1017 / S0016672397002954 PubMed Abstract | Full Text | CrossRef Full Text/Google Scholar
Crow, J. F., And Kimura, M. (1970). An Introduction to Population Genetics Theory. New York, NY: Harper And Row.
Google Scholar
Ohta, T., and Kimura, M. (1971). Desequilíbrio entre dois núcleos segregantes sob o fluxo constante de mutações em uma população finita. Genetics 68, 571-580.
PubMed Abstract | Full Text/Google Scholar
Wright, S. (1943). Isolamento à distância. Genetics 28, 114-138.
PubMed Abstract | Full Text | Google Scholar