filtros Kalman

o algoritmo usado para juntar os dados é chamado de filtro Kalman.

o filtro de Kalman é um dos algoritmos mais populares na fusão de dados. Inventado em 1960 por Rudolph Kalman, agora é usado em nossos telefones ou satélites para navegação e rastreamento. O uso mais famoso do filtro foi durante a missão Apollo 11 para enviar e trazer a tripulação de volta para a lua.

quando usar um filtro de Kalman ?

Um filtro de Kalman pode ser usado para dados de fusão para estimar o estado de um sistema dinâmico (evoluindo com o tempo) no presente (filtragem), o passado (suavização) ou futuro (previsão). Sensores embutidos em veículos autônomos emitem medidas que por vezes são incompletas e ruidosas. A imprecisão dos sensores (ruído) é um problema muito importante e pode ser tratado pelos filtros Kalman.

um filtro de Kalman é usado para estimar o estado de um sistema, denotado por X. Este vector é composto por uma posição p e uma velocidade v.

A cada estimativa, nós associar uma medida de incerteza P.

Através da realização de uma fusão de sensores, devemos levar em conta dados diferentes para o mesmo objeto. Um radar pode estimar que um pedestre está a 10 metros de distância, enquanto o Lidar estima que seja de 12 metros. O uso de filtros Kalman permite que você tenha uma idéia precisa para decidir quantos metros realmente é o pedestre, eliminando o ruído dos dois sensores.

um filtro Kalman pode gerar estimativas do Estado dos objetos ao seu redor. Para fazer uma estimativa, ela só precisa das observações atuais e da previsão anterior. O histórico de medição não é necessário. Esta ferramenta é, portanto, leve e melhora com o tempo.

How it looks like

State and uncertainty are represented by Gaussians.

Uma Gaussiana é uma função contínua em que a área é de 1. Isso nos permite representar probabilidades. Temos uma probabilidade de distribuição normal. A uni-modalidade dos filtros Kalman significa que temos um único pico de cada vez para estimar o estado do sistema.

temos uma média μ representa um estado e uma variância σ2 representa uma incerteza. Quanto maior a variação, maior a incerteza.

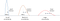
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Usamos as observações de nossos sensores para corrigir o estado previsto e obter uma estimativa mais precisa.

para fazer uma estimativa, um filtro de Kalman só precisa de observações atuais e da previsão anterior. O histórico de medição não é necessário.

Maths

a matemática por trás dos filtros de Kalman é feita de adições e multiplicações de matrizes. Temos duas fases: Previsão e atualização.

predição
nossa predição consiste em estimar um estado x’ e uma incerteza P ‘ no tempo t dos Estados X e P no tempo t-1.

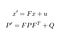
• F: Matriz de transição de t-1 para t
• ν: Ruído adicionado
• Q: Matriz de covariância incluindo o ruído

Atualizar
A fase de atualização, consiste em utilizar um z de medição a partir de um sensor para corrigir a nossa previsão e, assim, prever x e P.

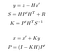
• y: Diferença entre a medida real e a previsão, ou seja, o erro.
• S: erro estimado do sistema
• H: matriz de transição entre o marcador do sensor e o nosso.
• R: Matriz de covariância relacionada com o ruído dos sensores (dada pelo fabricante do sensor).K: Kalman gain. Coeficiente entre 0 e 1, reflectindo a necessidade de corrigir a nossa previsão.

a fase de actualização permite estimar um x e um P mais próximos da realidade do que o que as medições fornecem.

um filtro Kalman permite previsões em tempo real, sem dados de antemão. Nós usamos um modelo matemático baseado na multiplicação de matrizes para cada vez definindo um estado x (posição, velocidade) e incerteza P.

Représentation Prior/Posterior

este diagrama mostra o que acontece num filtro de Kalman.

• Previstos estado de estimativa representa a nossa primeira estimativa, a nossa previsão fase. Estamos a falar de prior.a medição é a medida de um dos nossos sensores. Temos uma maior incerteza, mas o ruído dos sensores torna-a uma medição que é sempre difícil de estimar. Falamos de probabilidades.
• A estimativa de estado ideal é a nossa fase de actualização. A incerteza é que, desta vez, o mais fraco, acumulou informações e permitiu-nos gerar um valor mais seguro do que apenas com o nosso sensor. Este valor é o nosso melhor palpite. Falamos de posterior.

o que um filtro de Kalman implementa é na verdade uma regra de Bayes.

Em um filtro de Kalman, nós loop previsões a partir de medições. As nossas previsões são sempre mais precisas, uma vez que mantemos uma medida de incerteza e calculamos regularmente o erro entre a nossa previsão e a realidade. Somos capazes de multiplicar matrizes e fórmulas de probabilidade para estimar velocidades e posições de veículos ao nosso redor.

filtros”EXTENDIDOS/não desgastados” e não linearidade

surge um problema essencial. Nossas fórmulas matemáticas são todas implementadas com funções lineares do tipo y = ax + B.
Um filtro Kalman sempre funciona com funções lineares. Por outro lado, quando usamos um Radar, os dados não são lineares.

O Radar vê o mundo com três medidas de:

estes três valores fazem da nossa medição um não linear dada a inclusão do ângulo φ.o nosso objectivo aqui é converter os dados ρ, φ, ρ Para Dados Cartesianos (px, py, vx, vy).

Se introduzirmos dados não-lineares num filtro Kalman, o nosso resultado já não está na forma gaussiana uni-modal e já não podemos estimar a posição e a velocidade.

Então, podemos utilizar aproximações, que é por isso que nós estamos trabalhando em dois métodos:
– filtros de Kalman Estendido usar a Razão e a série de Taylor para linearizar o modelo.
– filtros Kalman sem cheiro usam uma aproximação mais precisa para linearizar o modelo.

Para lidar com a inclusão da não-linearidade pelo Radar, existem técnicas e permitir que os nossos filtros para estimar a posição e velocidade dos objetos que desejamos controlar.