Molecular Expressões: a Ciência, a Óptica, e Você: Luz e Cor – Refração da Luz
- Refração da Luz
- Questions or comments? Envie-nos um e-mail.
- © 1998-2021 by Michael W. Davidson and the Florida State University. Todos Os Direitos Reservados. Nenhuma imagem, Gráficos, scripts ou applets podem ser reproduzidos ou usados de qualquer forma sem a permissão dos detentores de direitos autorais. O uso deste site significa que você concorda com todos os Termos e condições legais estabelecidos pelos proprietários.
- This website is maintained by our Graphics & Web Programming Team in collaboration with Optical Microscopy at the National High Magnetic Field Laboratory.
- última modificação: sexta-feira, 13 de Novembro de 2015 às 02: 18 PM
- Contagem de acesso desde 10 de Março de 2003: 181405
- visite os sites dos nossos parceiros na educação:
Refração da Luz
Refração, ou desvio da luz, ocorre como a luz passa de um meio para outro meio com um índice de refração diferente. Refração é uma característica importante das lentes, permitindo-lhes focar um feixe de luz em um único ponto, e também é responsável por uma variedade de fenômenos familiares, tais como a distorção aparente de objetos parcialmente submersos na água.
Índice de refração é definido como a velocidade relativa a que a luz se move através de um material em relação à sua velocidade no vácuo. Por convenção, o índice de refração de um vácuo é definido como tendo um valor de 1.0. O índice de refração, n, de outros materiais transparentes é definido pela equação:
, onde c é a velocidade da luz, e v é a velocidade da luz no material. Uma vez que o índice de refração de um vácuo é definido como 1.0 e um vácuo é desprovido de qualquer material, os índices de refração de todos os materiais transparentes são, portanto, maiores que 1,0. Para fins mais práticos, o índice de refração da luz através do ar (1.0003) pode ser usado para calcular índices de refração de materiais desconhecidos. Os índices de refração de alguns materiais comuns são apresentados na Tabela 1 abaixo.
|
||||||||||||||||||||||
Table 1
It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Por exemplo, quando a luz passa de um meio menos denso, como o ar, para um meio mais denso, como a água, a velocidade a que a onda eletromagnética está viajando diminui. Alternativamente, quando a luz passa de um meio mais denso para um meio menos denso, a velocidade da onda aumenta.
O ângulo em que a luz refratada viaja, no entanto, depende tanto do ângulo de incidência como da composição do material em que entra. O normal pode ser definido como uma linha perpendicular ao limite entre duas substâncias. A luz passa para o limite de um ângulo com a normal e é refratada de acordo com a Lei de Snell:
, onde n representa os índices de refração do material 1 material e 2 e q simboliza os ângulos de luz viaja através destes materiais com relação à normal. Há vários pontos importantes que podem ser extraídos desta equação. Quando n(1) é maior que n (2), o ângulo de refração é sempre menor que o ângulo de incidência. Alternativamente, quando n (2) é maior que n(1) o ângulo de refração é sempre maior que o ângulo de incidência. Quando os dois índices de refração são iguais (n(1) = n (2)), então a luz é passada sem refração.
O conceito de índice de refração é ilustrado na Figura 1 abaixo, focando-se no caso da luz que passa do ar através do vidro e da água. Observe que enquanto ambos os feixes entram no material mais denso através do mesmo ângulo de incidência em relação ao normal (60 graus), a refração para o vidro é quase 6 graus maior do que a para a água devido ao índice de refração mais elevado do vidro.
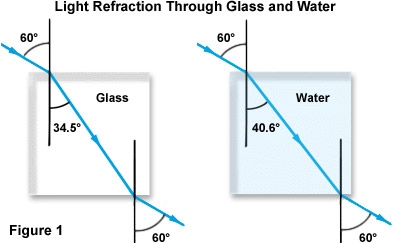
os Cientistas descobriram que o índice de refração varia com a freqüência de radiação ou comprimento de onda) da luz. Este fenômeno ocorre em conjunto com todos os meios transparentes e tem sido chamado de dispersão. Por conseguinte, ao medir o índice de refracção de uma substância transparente, deve ser identificado o comprimento de onda específico utilizado na medição. Abaixo, a Tabela 2 detalha a dispersão de três comprimentos de onda independentes em vários meios.
|
||||||||||||||||||||||||||
Table 2
The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Esta luz é chamada de espectro de linha D, e representa a luz amarela listada na Tabela 2 acima. Da mesma forma, os espectros de linhas F E C correspondem à luz azul e vermelha de comprimentos de onda específicos emitidos pelo hidrogênio. Estes espectros são fundamentais para o cálculo da dispersão, que pode ser quantitativamente definido como:
, onde n é o índice de refração do material em um determinado comprimento de onda designado por D, F, e, C, o que representam as linhas espectrais de sódio e hidrogênio, como discutido acima. A relação é tal que como o comprimento de onda da luz aumenta, o índice de refração diminui. No entanto, muitos fatores desempenham um papel na dispersão de vários materiais, incluindo sua composição elementar e molecular. Vários sólidos inorgânicos, como cromatos, dicromatos, cianetos, vanadatos e complexos de haletos, têm dispersões invulgarmente altas. No entanto, os substituintes orgânicos podem também contribuir para uma elevada dispersão.
| Interactive Java Tutorial | |||||||||||
|
|||||||||||
Refraction of light is particularly important in the construction and physics of lenses. Lembre-se, que quando o feixe de luz saiu do vidro e da água na Figura 1, ele foi novamente refratado no mesmo ângulo em que entrou no material. Este conceito é essencial no funcionamento das lentes, embora a forma da lente afeta significativamente a imagem resultante. Em uma lente convexa, como ilustrado abaixo na Figura 2, ondas de luz refletidas do objeto, neste caso uma girafa, são dobradas em direção ao centro óptico da lente e convergem no ponto focal.
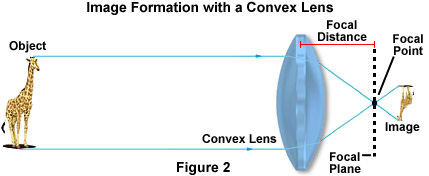
A posição relativa do objeto com respeito para a frente, ponto focal da lente determina como o objeto é espelhado. Se o objeto está além do dobro da distância do ponto focal, então ele parece menor e invertido e deve ser fotografado por uma lente adicional, a fim de ampliar o tamanho. No entanto, quando a imagem está mais próxima da lente do que o ponto focal, a imagem aparece vertical e maior, como pode ser facilmente demonstrado com uma lupa simples.
| Interactive Java Tutorial | |||||||||||
|
|||||||||||
Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Uma simples palhinha de beber num copo cheio de água, como ilustrado na Figura 3, é um excelente exemplo desta ocorrência. Neste exemplo, ondas de luz devem primeiro passar através da água, em seguida, através do limite vidro/água, e, finalmente, através do ar. As ondas de luz refletidas das extremidades da palha são refratadas em um grau maior do que aquelas que vêm do centro da palha, fazendo com que a palha pareça ampliada e ligeiramente distorcida.

O mesmo fenômeno pode ser utilizada para determinar o índice de refração de um líquido com um microscópio óptico. Para tal, deve ser colocada na superfície de vidro interior uma célula plana capaz de conter líquido com uma marca (ou graduações). Além disso, um dos oculares do microscópio deve ter uma retícula graduada inserida no plano de imagem primária para medir a largura da linha da marca na célula plana. Antes de adicionar o líquido de índice refrativo desconhecido à célula, o microscópio deve ser focado na marca na parte inferior da célula e uma medição da posição da marca na retícula anotada. Em seguida, deve ser adicionada uma pequena quantidade de líquido à célula e o microscópio reorientado para a marca (através do líquido) e uma nova medição feita. O microscópio deve então ser finalmente focado na superfície do líquido, e uma terceira leitura registrada medindo a posição da marca na retícula. O índice de refração do líquido desconhecido pode ser calculada utilizando a seguinte equação:
, onde D(medido) é a profundidade (a partir da superfície do líquido para a posição da marca na célula vazia), utilizando o microscópio e D(aparente) é a marca de medição com e sem líquido.
O ângulo crítico de reflexão é outro conceito chave no estudo da refração da luz e é ilustrado abaixo na Figura 4. Quando a luz passa através de um meio de alto índice de refração em um meio de menor índice de refração, o ângulo incidente das ondas de luz torna-se um fator importante. Se o ângulo incidente aumenta para além de um valor específico (dependente do Índice de refração dos dois meios), ele vai chegar a um ponto onde o ângulo é tão grande que nenhuma luz é refratada no meio do Índice de refração inferior.
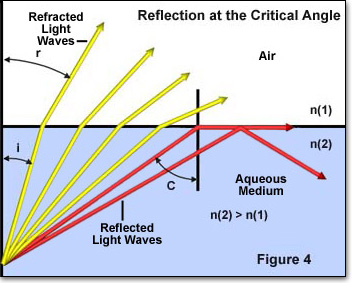
Na Figura 4, individuais raios de luz são representados por vermelho ou amarelo colorido setas mover-se de um meio de alto índice de refração (n(2)) para um de menor índice de refração (n(1)). O ângulo de incidência de cada raio de luz individual é denotado por i e o ângulo de refração por R. os quatro raios de luz amarelos todos têm um ângulo de incidência (i) baixo o suficiente para passar através da interface entre os dois meios. No entanto, os dois raios de luz vermelha têm ângulos incidentes que excedem o ângulo crítico (aproximadamente 41 graus) e são refletidos tanto na fronteira entre o meio ou de volta para o meio de índice de refração elevado. Este fenômeno ocorre quando o ângulo de refração (ângulo de r na Figura 4) torna-se igual a 90 graus e a lei de Snell se reduz a:
, onde (q) é agora denominado ângulo crítico C. Se o meio de menor índice de refração é o ar (n = 1.00), a equação reduz ainda mais a:
Como discutido anteriormente, uma outra característica importante da refração da luz é que o comprimento de onda da luz tem um impacto na quantidade de refração que ocorre dentro de uma média. Na verdade, a quantidade de refração que ocorre é inversamente proporcional ao comprimento de onda da luz incidente. Assim, comprimento de onda mais curto luz visível é refratado em um ângulo maior do que a luz de comprimento de onda mais longo. Conseqüentemente, quando a luz branca, que é composta de todas as cores no espectro visível, é passada através de um prisma de vidro, é dispersada em suas cores componentes de uma maneira que é dependente dos comprimentos de onda individuais. A luz visível de baixa frequência (600 nanômetros e maior) é refratada em um ângulo menor do que a luz de maior frequência, o que resulta em um efeito arco-íris, como ilustrado abaixo na Figura 5.
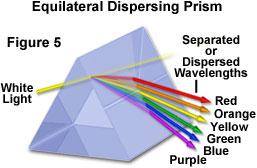
Este mesmo fenômeno também é responsável pela aberração cromática. Quando a luz branca é passada através de uma lente convexa simples, vários pontos focais surgem em estreita proximidade que correspondem às pequenas diferenças de índice de refração dos comprimentos de onda dos componentes. Este efeito tende a produzir halos coloridos (vermelho ou azul, dependendo do foco) em torno das imagens dos objetos. A correção desta aberração é geralmente realizada através do uso de combinações de dois ou mais elementos da lente compostos por materiais com propriedades dispersivas diferentes, tais como uma lente acromática construída com vidros de coroa e de pedra.
| Interactive Java Tutorial | |||||||||||
|
|||||||||||
Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. O exemplo mais comum é uma câmera, que é projetada para criar imagens aguçadas e focadas em uma emulsão de filme ou na superfície de um dispositivo acoplado de carga (CCD) para produzir uma imagem precisa. Outros dispositivos ópticos que exploram essas características da luz incluem microscópios e telescópios, que permitem a visualização de objetos que são invisíveis para o nu olho humano, independentemente se eles são localizados na cabeça de um alfinete ou em uma galáxia distante.
autores contribuintes
Mortimer Abramowitz-Olympus America, Inc., Dois Centros Corporativos., Melville, New York, 11747.Shannon H. Neaves and Michael W. Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
BACK TO LIGHT and COLOR
Questions or comments? Envie-nos um e-mail.
© 1998-2021 by Michael W. Davidson and the Florida State University. Todos Os Direitos Reservados. Nenhuma imagem, Gráficos, scripts ou applets podem ser reproduzidos ou usados de qualquer forma sem a permissão dos detentores de direitos autorais. O uso deste site significa que você concorda com todos os Termos e condições legais estabelecidos pelos proprietários.
This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the National High Magnetic Field Laboratory.
última modificação: sexta-feira, 13 de Novembro de 2015 às 02: 18 PM
Contagem de acesso desde 10 de Março de 2003: 181405
visite os sites dos nossos parceiros na educação: