Prealgebra
Resultados da Aprendizagem
- Encontrar a área, base e altura de um triângulo
- a Encontrar o comprimento de um lado de um triângulo dado perímetro e dois outros comprimentos
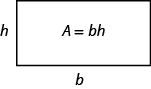
agora sabemos como encontrar a área de um retângulo. Podemos usar este fato para nos ajudar a visualizar a fórmula para a área de um triângulo. No retângulo abaixo, nós rotulamos o comprimento b e a largura h, então a área é bh.
a área de um retângulo é a base, b, vezes a altura, h.
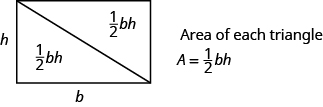
Podemos dividir este retângulo em dois triângulos congruentes (veja a imagem abaixo). Triângulos que são congruentes têm comprimentos laterais e ângulos idênticos, e assim suas áreas são iguais. A área de cada triângulo é metade da área do retângulo, ou \frac{1}{2}bh. Este exemplo nos ajuda a ver por que a fórmula para a área de um triângulo é a=\frac{1}{2}bh.
um retângulo pode ser dividido em dois triângulos de área igual. A área de cada triângulo é metade da área do retângulo.
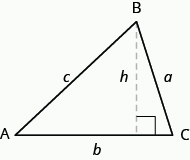
a fórmula para a área de um triângulo é a = \frac{1}{2}bh, onde b é a base e h é a altura.para encontrar a área do triângulo, você precisa saber sua base e altura. A base é o comprimento de um lado do triângulo, geralmente o lado no fundo. A altura é o comprimento da linha que liga a base ao vértice oposto, e faz um ângulo \text{90}^ \circ com a base. A imagem abaixo mostra três triângulos com a base e a altura de cada um marcado.
a altura h de um triângulo é o comprimento de um segmento de linha que liga a base ao vértice oposto e faz um ângulo \text{90}^ \circ com a base.

propriedades do triângulo
para qualquer triângulo \Delta ABC, a soma das medidas dos ângulos é \text{180}^ \circ.
m\angle{A}+M\angle{b}+m\angle{C}=180^\circ
O perímetro de um triângulo é a soma dos comprimentos dos lados.
P=a+b+c
A área de um triângulo é metade da base, b, vezes a altura, h.
A=\frac{1}{2}bh
exemplo
encontrar a área de um triângulo cuja base tem 11 polegadas e cuja altura é de 8 polegadas.
Solução
| Passo 1. Lê o problema. Desenhe a figura e rotule-a com a informação dada. |  |
| Passo 2. Identifique o que procura. | a área do triângulo |
| Passo 3. Nome. Escolha uma variável para representá-la. | let a = area of the triangle |
| Step 4.Traduzir.
escreva a fórmula apropriada. Substituto. |
 |
| Passo 5. Resolve a equação. | a = 44 polegadas quadradas. |
| Passo 6. Verificar:
A=\frac{1}{2}bh 44\stackrel{?{ = } \frac{1}{2}(11)8 44=44\marca de verificação |
|
| Step 7. Responde à pergunta. | a área é de 44 polegadas quadradas. |
tentar
exemplo
O perímetro de um jardim triangular é de 24 pés. O comprimento de dois lados é de 4 pés e 9 pés. Quanto tempo dura o terceiro lado?
tentar
exemplo
A área de um triangular igreja de janela é de 90 metros quadrados. A base da janela é de 15 metros. Qual é a altura da janela?
tentar
Isósceles e Equilátero Triângulos
Além disso, o direito do triângulo, alguns outros triângulos têm nomes especiais. Um triângulo com dois lados de igual comprimento é chamado de triângulo isósceles. Um triângulo que tem três lados de comprimento igual é chamado de triângulo equilátero. A imagem abaixo mostra ambos os tipos de triângulos.
em um triângulo isósceles, dois lados têm o mesmo comprimento, e o terceiro lado é a base. Em um triângulo equilátero, todos os três lados têm o mesmo comprimento.
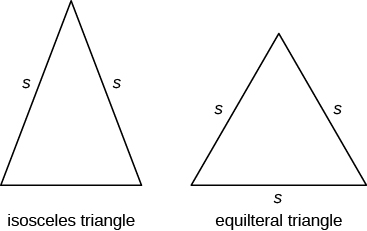
isósceles e triângulos equiláteros
um triângulo isósceles tem dois lados do mesmo comprimento.um triângulo equilátero tem três lados de igual comprimento.
exemplo
o perímetro de um triângulo equilátero é de 93 polegadas. Encontre o comprimento de cada lado.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. O cachecol será um triângulo isósceles com uma base de
60 polegadas. Quanto tempo ela pode fazer os dois lados iguais?








