An integral part of fluid dynamics is vorticity. Heuristicamente, mede a rotação local de uma parcela fluida. Para objetos sólidos não falamos da vorticidade de um objeto, mas sim da sua velocidade angular. Estes dois conceitos estão relacionados, mas a vorticidade é mais útil quando se discute objetos rotativos que deformam, como um fluido faz.

a vorticidade de um dado campo de velocidade dentro de um determinado plano, é calculada escolhendo quaisquer dois eixos ortogonais nesse plano e adicionando a velocidade angular de cada eixo. Em um objeto sólido, ou um fluido que gira como um objeto sólido (apropriadamente chamado rotação de corpo sólido), a vorticidade é o dobro da velocidade angular desde que cada eixo gira na mesma taxa. No entanto, em um fluido os dois eixos podem rodar em taxas muito diferentes e até mesmo direções diferentes! É mesmo possível que cada eixo possa rodar ainda que a vorticidade da rede seja zero (ver vórtice irrotacional).

Se o movimento de um fluido é estritamente confinado a estar em um plano, então o vetor de vorticidade é tomado para ser ortogonal ao plano e não pode mudar de direção (ou inclinação). O único aspecto da vorticidade que pode mudar é a sua magnitude. Acredita-se que esta transferência de energia para escalas maiores está ligada à formação da Grande Mancha Vermelha em Júpiter.

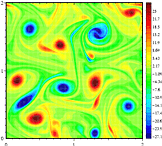
Em três dimensões movimento fluido a vorticity vetor de três dimensões em que possui componentes em paralelo para cada eixo, x, y e z: a componente z é paralelo ao eixo z e descreve a taxa de rotação no plano xy. É por causa desta dicotomia que existe uma diferença qualitativa no comportamento entre turbulência bidimensional e turbulência tridimensional. No primeiro há uma tendência para vórtices se juntarem e formarem vórtices maiores, enquanto no segundo os movimentos vórticos são dilacerados e a energia cascata para as menores escalas onde é então difundida.

Matematicamente, o vorticity de uma dada velocidade do campo

é definido para ser a onda da velocidade campo, e geralmente é indicado com a letra grega omega,

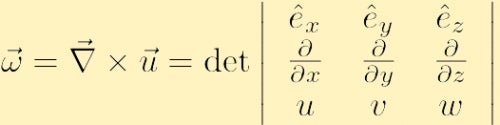
, onde temos usado o convencional nabla símbolo para a gradiente:

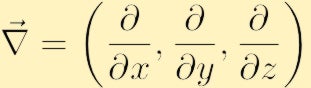
No componente de forma a vorticity é encontrado expandindo o determinante acima,

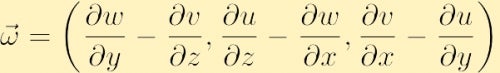
Outro aspecto importante da dinâmica dos fluidos está relacionado ao vorticity é a circulação. Ao contrário da vorticidade, que é uma propriedade local, definida em cada ponto do espaço, a circulação é uma propriedade global, definida pela integração de uma propriedade do fluido sobre uma curva. Em particular, se você escolher qualquer contorno fechado e indicar com a letra C(t) a circulação em torno de C(t), no sentido anti-horário, é uma quantidade escalar denotado com,

é definido como,

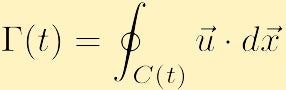
o que pode ser uma função do tempo, como pode o contorno fechado.vamos tirar um momento para explicar o que isso está dizendo fisicamente. Em cada ponto do contorno(t) encontramos o componente da velocidade tangente à curva e multiplicamos este escalar por um comprimento infinitesimal.; projetar a velocidade na tangente necessariamente dará uma magnitude entre a velocidade nessa posição e zero. Se a velocidade é tangente à curva, então obtemos mais ou menos a velocidade de, se a velocidade é ortogonal à curva, obtemos zero. Então integramos esta quantidade, uma maneira diferente de dizer somando um número infinito de coisas, em torno do contorno para que adicionemos a contribuição de cada ponto. A partir disso, verificamos que a circulação ao longo de um contorno C (t) é a quantidade de fluxo em torno do contorno (t); um resultado positivo ou negativo corresponde à circulação no Sentido DOS ponteiros do relógio ou no Sentido DOS ponteiros do relógio, respectivamente. Um caso extremo é onde o campo de velocidade está perpendicular à curva C(t) e, consequentemente, não há circulação, uma vez que o fluxo está sempre cruzando o contorno e nunca fluindo ao longo do contorno. Para obter uma circulação não-Zero deve haver alguma parte da curva onde o fluxo está ao longo do contorno fechado.

Se o campo de velocidade é lisa e não há singularidades dentro de C(t), então podemos usar Stokes’ Integral Teorema do cálculo vetorial para reescrever a circulação como,

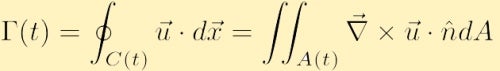
a, onde A é a área contida dentro do contorno C e ä é a unidade do vetor normal ao areaA.

Antes de contemplarmos esta nova equação para a circulação, é útil compreender o significado físico do Teorema de Stokes, onde o campo vetorial é a velocidade. Na dupla integral acima computamos a vorticidade em cada ponto dentro do contorno e então somamos a vorticidade sobre todos esses pontos em um(t). Na integral única sobre o contorno fechado estamos computando o fluxo ao longo do limite da área. O teorema de Stokes então afirma que essas quantidades são iguais, e assim que se há vorticidade média dentro de uma área, o que deve então significar que a área tem uma taxa de rotação não-Zero, deve haver consequentemente uma circulação líquida ao longo do perímetro desse limite.

do Teorema do valor médio do cálculo podemos substituir o integrador na integral dupla por um valor médio, que corresponde à componente média da ortogonal de vorticidade ao plano no qual C(t) se encontra. Assim, a segunda interpretação da circulação é que é a vorticidade média vezes a área contida dentro de C(t). Em vez de computar a circulação no contorno fechado C(t) podemos computar a vorticidade média normal para A(t) e multiplicar isso pela área dentro. Se você considerar o caso especial onde a vorticidade está em toda parte constante a circulação seria a magnitude da vorticidade vezes a área contida dentro.

um ponto vórtice é um vórtice que não tem área, o que significa que a vorticidade está presente apenas em um único ponto. Para estudar os vórtices do ponto nós assumiremos primeiramente que nós temos um fluxo 2D incompressível. (Vórtices de ponto também são por vezes referidos como vórtices de linha quando vistos em 3D.)

Depois de alguns cálculos que determinam que a velocidade do campo que é gerada por um ponto de vórtice, em forma complexa, que está localizado em z0 é dada por (onde Gamma zero é a circulação em torno do ponto de vortex, que é muitas vezes referida como a força do ponto de vortex):

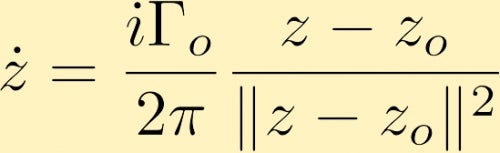
A velocidade do campo gerado por um ponto de vórtice pode causar um outro ponto de vórtice para mover. Aqui estão alguns exemplos disso: Os dois vórtices de pontos, tanto positivos como de igual magnitude, os dois vórtices de pontos, ambos positivos, mas um tem triplicado a força do outro e um vórtice de ponto é negativo com o dobro da magnitude do outro que é positivo . Outra possibilidade é considerar dois vórtices pontos da mesma magnitude, mas sinal oposto.

isto pode ser estendido A qualquer número de vértices, N. A equação de movimento na forma complexa para um ponto vórtice alfa é dada por:

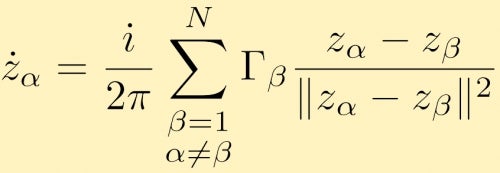
olhar para as interações de vórtices de pontos é um problema muito interessante que é difícil de fazer analiticamente, especialmente porque o número de vórtices de pontos aumenta. Simulações numéricas de interações de pontos vórtices são, portanto, muito comuns. Uma aplicação útil de simulações de vórtice de ponto grande é se você olhar para grandes conjuntos de vórtices de ponto que simula vórtices com área finita. Aqui estão descrições e os resultados de várias simulações de vórtice de ponto grande. Neste caso, temos dois grandes grupos de vórtices de pontos de igual força que se fundem. No próximo caso começamos com um anel de pontos agrupados.

para encontrar uma equação para a evolução da vorticidade começamos com a equação do momento. Na equação do momento, o termo advectivo pode ser reescrito da seguinte forma:

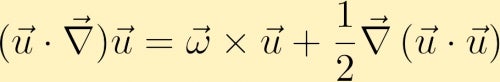
calculamos a curva da equação do momento e através de algumas identidades vectoriais obtemos a equação da vorticidade:

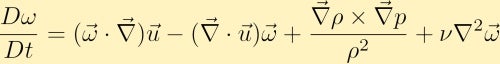
a equação de vorticidade mostra como a vorticidade pode ser gerada em um fluido. Sem perda de generalidade, assumiremos que inicialmente só temos vórtice na direção z. A partir disso podemos ver como cada um dos quatro termos diferentes pode alterar a vorticidade.

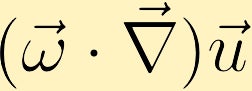
Se houver uma mudança na velocidade com a direção da vorticidade existente, a vorticidade pode ser gerada.

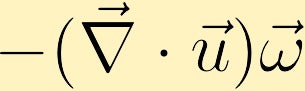
Se uma parcela fluida estiver em expansão e a vorticidade for positiva a vorticidade da parcela fluida irá diminuir e se a parcela estiver a contrair a vorticidade irá aumentar.

camadas de Fluido de densidade constante (isopycnals) pretende coincidir com as camadas de pressão constante (linhas isobáricas). Se essas camadas não coincidem, o fluido começa a rodar para fazer com que elas se alinhem, o que faz com que a vorticidade seja gerada. (No exemplo começamos com vorticidade zero.)

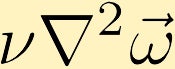
forças viscosas causam a difusão da vorticidade. (No exemplo começamos com um ponto de vorticidade infinita no centro.)