proiect Nayuki
definiție: secvența Fibonacci este definită ca \(F(0) = 0\), \(F (1) = 1\), și \(F(n) = F(n-1) + F(N-2)\) Pentru \(n 2\). Deci secvența (începând cu \(F (0)\)) este 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
dacă vrem să calculăm un singur termen în secvență (de exemplu, \(F(n)\)), există câțiva algoritmi pentru a face acest lucru. Unii algoritmi sunt mult mai rapizi decât alții.
algoritmi
manual recursiv (extrem de lent)
naiv, putem executa direct recurența așa cum este dat în definiția matematică a secvenței Fibonacci. Din păcate, este iremediabil de lent: folosește \(spațiul de stivă (N)\) și \ (operații aritmetice (n)\), unde \ (int = \ frac {\sqrt{5} + 1}{2}\) (raportul de aur). Cu alte cuvinte, numărul de operații de calculat \(F(n)\) este proporțional cu răspunsul numeric final, care crește exponențial.
Programare dinamică (lentă)
ar trebui să fie clar că dacă am calculat deja \(F(k-2)\) și \(F(k-1)\), atunci le putem adăuga pentru a obține \(F(k)\). Apoi, adăugăm \(F(k-1)\) și \(F(k)\) pentru a obține \(F (k+1)\). Repetăm până ajungem la \(k = n\). Majoritatea oamenilor observă automat acest algoritm, mai ales atunci când calculează Fibonacci manual. Acest algoritm ia \((1)\) spațiu și \ ((n)\) operații.
Exponențierea matricei (rapidă)
algoritmul se bazează pe această identitate inocentă (care poate fi dovedită prin inducție matematică):
\( \left^n = \left \).
este important să folosiți exponențierea prin pătrat cu acest algoritm, deoarece altfel degenerează în algoritmul de programare dinamică. Acest algoritm ia \(sec (1)\) spațiu și\(SEC (\log n)\) operațiuni. (Notă: Numărăm numărul de operații aritmetice bigint, nu operații de cuvinte cu lățime fixă.)
dublare rapidă (mai rapidă)
dată \(F(k)\) și \(F(K+1)\), putem calcula următoarele:
\(\begin{align}F(2K)&= f(k) \left. \\F(2k+1) &= F(k+1)^2 + F (k)^2.\end{align}\)
aceste identități pot fi extrase din algoritmul de exponențiere a matricei. Într-un sens, acest algoritm este algoritmul de exponențiere a matricei cu calculele redundante eliminate. Ar trebui să fie un factor constant mai rapid decât exponențierea matricei, dar complexitatea asimptotică a timpului este în continuare aceeași.
rezumat: cei doi algoritmi Fibonacci rapizi sunt exponențierea matricei și dublarea rapidă, fiecare având o complexitate asimptotică a operațiilor aritmetice bigint. Ambii algoritmi folosesc multiplicarea, astfel încât acestea devin și mai rapide atunci când se utilizează multiplicarea Karatsuba. Ceilalți doi algoritmi sunt lenți; folosesc doar adunare și fără multiplicare.
cod sursă
implementările sunt disponibile în mai multe limbi:
-
Java: FastFibonacci.java (toate 3 algoritmi, calendarul de referință, programul principal runnable)
-
Python: fastfibonacci.py (numai funcția de dublare rapidă)
-
Haskell: fastfibonacci.hs (numai funcția de dublare rapidă)
-
C#: FastFibonacci.cs (dublarea rapid numai, programul principal runnable)
(necesită. NET Framework 4.0 sau mai sus; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
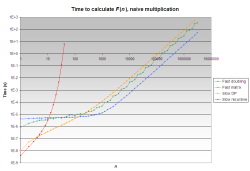
All algorithms, naive multiplication
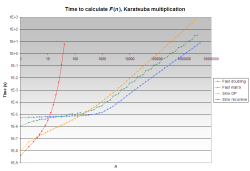
All algorithms, Karatsuba multiplication
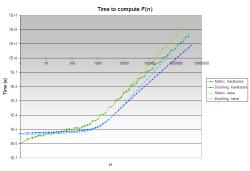
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive |
|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||
| 3 981 072 | 7 654 000 000 |
toate timpurile sunt date în nanosecunde (ns), date la 4 cifre semnificative. Toate testele de mai sus au fost efectuate pe Intel Core 2 Quad Q6600 (2.40 GHz) folosind un singur fir, Windows XP SP 3, Java 1.6.0_22.
dovezi
Exponențierea matricei
vom folosi inducția slabă pentru a dovedi această identitate.
caz de bază
pentru \(N = 1\), clar \( \stânga^1 = \stânga \).
etapa de inducție
presupuneți pentru \(N 1\) că \( \stânga^n = \stânga \). Apoi:
\(\stânga^{n+1} \\= \stânga^n \stânga \\= \stânga \stânga \\= \stânga \\= \stânga.\)
dublare rapidă
vom presupune faptul că metoda de exponențiere a matricei este corectă pentru toți\(n.
\(\stânga \\= \stânga^{2n} \\= \stânga( \stânga^n \dreapta)^2 \\= \stânga^2 \\= \stânga.\)
prin urmare, prin echivalarea celulelor din matrice:
\(\begin{align}F(2n+1)&= F(n+1)^2 + F(n)^2. \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)