În epoca lumii digitale, vom vedea recomandare în fiecare vreme domeniu este site-ul de e-commerce sau site-ul de divertisment sau site-uri de rețele sociale. Recomandarea nu numai că oferă utilizatorului alegerea recomandată (pe baza activității anterioare), dar spune și despre comportamentul utilizatorului (analiză sentimentală sau emoție ai).

deci, în primul rând, să înțelegem ce recomandare este. Acesta este, practic, recomanda element de utilizator pe baza de căutare/activitate din trecut.

Figura 1 prezintă recomandarea Amazon pe baza istoricului de navigare din trecut și a căutărilor din trecut. Deci, putem spune că recomandarea este practic prezicerea comportamentului viitor bazat pe comportamentul trecut. Există două tipuri de abordări care sunt utilizate în sistemul de recomandări

1 – filtrarea bazată pe conținut

2 – filtrarea bazată pe colaborare

filtrarea bazată pe conținut-

se bazează pe ideea de a recomanda elementul utilizatorului K, care este similar cu elementul anterior foarte apreciat de K. conceptul de bază în filtrarea bazată pe conținut este TF-IDF (Term frequency — inverse document frequency), care este utilizat pentru a determina importanța documentului/cuvântului/filmului etc. Filtrarea bazată pe conținut arată transparență în recomandare, dar spre deosebire de filtrarea colaborativă nu poate funcționa eficient pentru date mari

filtrarea bazată pe colaborare

se bazează pe ideea că persoanele care împărtășesc același interes pentru anumite tipuri de articole vor împărtăși, de asemenea, același interes pentru alte tipuri de articole, spre deosebire de conținutul bazat, care se bazează practic pe metadate în timp ce se ocupă de activitatea din viața reală. Acest tip de filtrare este flexibil pentru cea mai mare parte a domeniului (sau putem spune că este domeniu gratuit), dar din cauza problemei de pornire la rece, raritatea datelor (care a fost gestionată de factorizarea matricei), acest tip de algoritm se confruntă cu un anumit obstacol în unele scenarii.

factorizarea matricei

factorizarea matricei vine în lumina reflectoarelor după competiția Netflix (2006), când Netflix a anunțat un premiu în bani de 1 milion de dolari celor care își vor îmbunătăți performanța medie pătrată cu 10%. Netflix a oferit un set de date de instruire de 100.480.507 evaluări pe care 480.189 de utilizatori le-au acordat pentru 17.770 de filme.

factorizarea matricei este metoda de filtrare bazată pe colaborare în care matricea m*n este descompusă în m*k și k*N . Acesta este utilizat în principal pentru calcularea funcționării matricei complexe. Diviziunea matricei este astfel încât, dacă înmulțim matricea factorizată, vom obține matricea originală așa cum se arată în Figura 2. Acesta este folosit pentru a descoperi caracteristici latente între două entități (poate fi folosit pentru mai mult de două entități, dar acest lucru va veni sub factorizare tensor)

descompunerea matricei poate fi clasificată în trei tipuri-

1 – LU descompunere — descompunerea matricei în matricea l și U unde L este matricea triunghiulară inferioară și U este matricea triunghiulară superioară, utilizată în general pentru găsirea coeficientului de regresie liniară. Această descompunere a eșuat dacă matricea nu se poate descompune ușor

descompunerea matricei 2 – QR – descompunerea matricei în Q și R unde Q este matrice pătrată și R este matrice triunghiulară superioară (nu este necesar pătrat). Folosit pentru analiza sistemului eigen

descompunerea 3 – Cholesky – aceasta este cea mai utilizată descompunere în învățarea automată. Utilizat pentru calcularea liniară cel mai mic pătrat pentru regresie liniară

factorizarea matricei poate fi utilizată în diverse domenii, cum ar fi recunoașterea imaginii, recomandare. Matrice utilizate în acest tip de problemă sunt, în general, rare, deoarece există șanse ca un utilizator ar putea evalua doar unele filme. Există diverse aplicații pentru factorizarea matricei, cum ar fi reducerea dimensionalității (pentru a afla mai multe despre reducerea dimensionalității, vă rugăm să consultați Blestemul dimensionalității), descompunerea valorii latente

declarație de problemă

în tabelul 1 avem 5 utilizatori și 6 filme în care fiecare utilizator poate evalua orice film. După cum putem vedea că Henry nu a evaluat pentru Thor și Rocky în mod similar Jerry nu a evaluat pentru Avatar. În scenariul din lumea reală, aceste tipuri de matrice pot fi matrice extrem de rare

Declarația noastră problemă este că trebuie să aflăm evaluări pentru filmele neevaluate așa cum se arată în tabelul 1

tabelul 1 – setul de date Film

ca scopul nostru de a găsi de rating a utilizatorului de factorizare matrice, dar înainte de asta trebuie să treacă prin descompunerea valorii singulare (SVD), deoarece factorizarea matrice și SVD sunt legate între ele

/ p >

SVD și Matrix factorization

înainte de a merge la adâncimea SVD permite mai întâi să înțeleagă ce este K și transpune(K). Dacă efectuăm PCA pe matricea K (Tabelul 1) obținem tot vectorul utilizator. Mai târziu putem pune acești vectori în coloana matricei U și dacă efectuăm PCA pe transpunere(K) obținem tot vectorul filmului care devine coloană pentru matricea M.

deci, în loc să efectuăm PCA pe K și să transpunem(K) separat, putem folosi SVD care poate efectua PCA pe K și transpune(K) într-o singură fotografie. SVD este practic matricea k factorizată în matricea U, matricea M și matricea diagonală:

unde K este matricea originală, U este matricea utilizatorului,M este matricea filmului, iar cea din mijloc este matricea diagonală

de dragul simplității, putem elimina matricea diagonală pentru o vreme, astfel încât noua ecuație devine:

lasa R este de rating definit pentru utilizator U și elementul i, p este rândul de M pentru un utilizator și Q este coloana de transpune(u) pentru un anumit element i. deci ecuația va deveni:

Notă — Dacă K este o valoare densă a matricei decât m va fi vectorul propriu al K*transpose(K), în mod similar valoarea U va fi vectorul propriu al transpose(k)*k dar matricea noastră este matrice rară nu putem calcula u și m prin această abordare

deci, aici pentru a găsi matricea m și U . O modalitate este de a inițializa valoarea aleatorie La M și U și comparați-o cu matricea originală K dacă valorile sunt apropiate de K decât opriți procedura altfel minimizați valoarea U și M până când sunt aproape de K . Procesul acestor tipuri de optimizare se numește coborâre gradient

Figura 3: gradient descent flow chart

deci, sarcina noastră de bază este de a minimiza funcția medie de eroare pătrată care poate fi reprezentată ca :

As our main task is to minimize the error i.e. trebuie să găsim în ce direcție trebuie să mergem pentru că trebuie să o diferențiem, prin urmare noua ecuație va deveni

prin urmare, valoarea actualizată pentru P și u va deveni acum:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Pe baza acestei linii de decizie putem distinge distribuția datelor

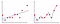
figura 4: underfit vs overfit

în figura 2 primul grafic este locul în care modelul este montat liniar, în timp ce în al doilea grafic este echipat cu grad polinomial. La prima vedere, se pare că al doilea complot este mult mai bun decât primul complot, deoarece oferă o precizie de 99% asupra datelor de antrenament, dar dacă introducem date de testare și oferim o precizie de 50% asupra datelor de testare . Acest tip de problemă se numește suprasolicitare și pentru a depăși această problemă introducem un concept numit regularizare.

ca overfitting problemă este comună în mașină de învățare, astfel încât există două tipuri de abordare regularizare, care pot fi utilizate pentru a elimina overfitting

1 – L1 regularizare

2 – L2 regularizare

L1 regularizare adăuga magnitudine liniară a coeficientului ca termen de penalizare în timp ce în L2 se adaugă magnitudine pătrată a coeficientului la funcția de pierdere / funcția de eroare (așa cum sa discutat mai sus). L1 întoarcere matrice rare în timp ce L2 nu. Regularizarea L1 funcționează bine în selectarea caracteristicilor în matricea rară.

în setul de date recomandare, de asemenea, există șanse mari de overfitting de date. Deci, pentru a elimina problema overfitting putem adăuga L2 regularizare (ca matrice este deja rare nu avem nevoie de L1 regularizare aici)în funcția de pierdere, prin urmare, noua ecuație a funcției de pierdere va fi:

din nou, putem găsi gradient pe MSE actualizate și să obțină puncte actualizate urmând aceeași abordare așa cum sa discutat mai sus

un lucru important să fie luate în considerare în scenariul de mai sus matricea P și q sunt non-negative, prin urmare, aceste tipuri de factorizare este, de asemenea, numit non-negativ factorizare. Deoarece factorizarea non-negativă extrage automat informații pentru setul non-negativ de vector. NMF este utilizat pe scară largă în procesarea imaginilor ,extragerea textului, analiza datelor cu dimensiuni ridicate