i en tid präglad av digital värld, ser vi rekommendation i varje område väder det är e-handel webbplats eller underhållning webbplats eller sociala nätverk webbplatser. Rekommendation ger inte bara Användaren sitt rekommenderade val (baserat på tidigare aktivitet) men det berättar också om användarbeteende (sentimental analys eller emotion AI).

så först, låt oss förstå vilken rekommendation som är. Det är i grunden rekommendera objekt till användaren baserat på dess tidigare sökning/aktivitet.

Figur 1 berättar Amazons rekommendation baserat på tidigare webbhistorik och tidigare sökningar. Så vi kan säga att rekommendation i princip förutsäger framtida beteende baserat på tidigare beteende. Det finns två typer av tillvägagångssätt som används i rekommendationssystem

1-innehållsbaserad filtrering

2-samarbetsbaserad filtrering

innehållsbaserad filtrering-

den bygger på tanken att rekommendera objektet till användaren K som liknar föregående objekt högt betygsatt av K. grundläggande koncept i innehållsbaserad filtrering är TF — IDF (Term frequency-inverse document frequency), som används för att bestämma vikten av dokument/ord/film etc. Innehållsbaserad filtrering visar öppenhet i rekommendationen men till skillnad från samarbetsfiltrering kan den inte fungera effektivt för stora data

samarbetsbaserad filtrering

den bygger på tanken att personer som delar samma intresse för vissa typer av objekt också kommer att dela samma intresse för någon annan typ av objekt till skillnad från innehållsbaserat som i grunden är beroende av metadata medan det handlar om verklig aktivitet. Denna typ av filtrering är flexibel för det mesta av domänen (eller vi kan säga att den är domänfri) men på grund av kallstartproblem, data sparsity (som hanterades av matrisfaktorisering) står denna typ av algoritm inför något bakslag i något scenario.

Matrix factorization

Matrix factorization kommer i rampljuset efter Netflix-tävlingen (2006) när Netflix tillkännagav en prispengar på 1 miljon dollar till dem som kommer att förbättra sin root mean square-prestanda med 10%. Netflix tillhandahöll en träningsdatauppsättning på 100 480 507 betyg som 480 189 användare gav till 17 770 filmer.

matrisfaktorisering är den samarbetsbaserade filtreringsmetoden där matris m*n sönderdelas i m*k och k*n . Det används i grunden för beräkning av komplex matrisoperation. Uppdelning av matris är sådan att om vi multiplicerar faktoriserad matris kommer vi att få originalmatris som visas i Figur 2. Den används för att upptäcka latenta funktioner mellan två enheter (kan användas för mer än två enheter men detta kommer att komma under tensorfaktorisering)

Matrisnedbrytning kan klassificeras i tre Typ-

1 – Lu — sönderdelning-sönderdelning av matris till L-och U-matris där L är lägre triangulär matris och U är övre triangulär matris, som vanligtvis används för att hitta koefficienten för linjär regression. Denna sönderdelning misslyckades om matrisen inte lätt kan ha sönderdelats

2-QR-matrisnedbrytning-sönderdelning av matrisen i Q och R där Q är kvadratisk matris och R är övre triangulär matris (inte nödvändig kvadrat). Används för egensystemanalys

3-Cholesky sönderdelning – detta är den mest använda sönderdelningen i maskininlärning. Används för att beräkna linjär minsta kvadrat för linjär regression

matrisfaktorisering kan användas i olika domäner såsom bildigenkänning, rekommendation. Matris som används i denna typ av problem är i allmänhet gles eftersom det finns chans att en användare bara kan betygsätta vissa filmer. Det finns olika applikationer för matrisfaktorisering såsom Dimensionalitetsreduktion (för att veta mer om dimensionalitetsreduktion, se Curse of Dimensionality), latent värdenedbrytning

Problemuttalande

i Tabell 1 har vi 5 användare och 6 filmer där varje användare kan betygsätta vilken film som helst. Som vi kan se att Henry inte betygsatte för Thor och Rocky på samma sätt betygsatte Jerry inte för Avatar. I verkliga världen scenario dessa typer av matris kan vara mycket gles matris

vårt problem uttalande är att vi måste ta reda på betyg för unrated filmer som visas i Tabell 1

som vårt mål att hitta betyg av användaren genom matrisfaktorisering men innan det måste vi gå igenom Singular Value Decomposition (SvD) eftersom matrisfaktorisering och SvD är relaterade till varandra

SVD och matrisfaktorisering

innan du går till djupet av SVD kan du först förstå vad som är K och transponera(K). Om vi utför PCA på matris K (Tabell 1) får vi all användarvektor. Senare kan vi sätta dessa vektorer i kolumn av matris U och om vi utför PCA på transponera (K) får vi all filmvektor som blir kolumn för matris M.

så istället för att utföra PCA på K och transponera(K) separat kan vi använda SVD som kan utföra PCA på K och transponera(K) i ett enda skott. SVD är i grunden faktoriserad matris K till matris U, matris M och diagonal matris:

där K är originalmatris, U är användarmatris,m är filmmatris och den mellersta är Diagonal matris

För enkelhetens skull kan vi ta bort diagonal matris ett tag så ny ekvation blir:

låt R är rating definieras för användaren U och punkt i, P är raden av M för en användare och Q är kolumnen transponera(u) för ett visst objekt i. så ekvationen blir:

Obs — Om k är tät matrisvärde än M kommer att vara egenvektor av k*transponera(K), på samma sätt värdet av U kommer att vara egenvektor av transponera(k)*k men vår matris är gles matris kan vi inte beräkna U och m med detta tillvägagångssätt

Så här är vår uppgift att hitta Matrix M och u . Ett sätt är att initiera slumpmässigt värde till M och U och jämföra det med originalmatris K om värdet är nära K än stoppa proceduren annars minimera värdet på U och M tills de är nära K . Processen för denna typ av optimering kallas gradient descent

så vår grundläggande uppgift är att minimera den genomsnittliga kvadratfelfunktionen som kan representeras som :

As our main task is to minimize the error i.e. vi måste hitta i vilken riktning vi måste gå för att vi måste skilja det, därför kommer ny ekvation att bli

därför kommer det uppdaterade värdet för P och u nu att bli:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Baserat på den beslutslinjen kan vi skilja fördelningen av data

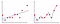
i Figur 2 första plot är där modellen är monterad linjärt medan den i andra plot är utrustad med polynomgrad. Vid första utseendet ser det ut som att andra tomten är mycket bättre än första tomten eftersom det ger 99% noggrannhet på träningsdata men vad händer om vi introducerar testdata och det ger 50% noggrannhet på testdata . Denna typ av problem kallas överfitting och för att övervinna detta problem introducerar vi ett koncept som kallas regularisering.

som överfitting problem är vanligt i maskininlärning så det finns två typer av regularisering tillvägagångssätt som kan användas för att ta bort överfitting

1 – L1 regularisering

2 – L2 regularisering

L1 regularisering lägga linjär magnitud av koefficienten som straff sikt medan i L2 det lägga kvadratisk magnitud av koefficienten till förlust funktion/fel funktion (som diskuterats ovan). L1 returnerar glesa matriser medan L2 inte gör det. L1 regularisering fungerar bra i funktionsval i gles matris.

i rekommendationsdataset finns det också stora chanser att överfitta data. Så för att ta bort överfittningsproblemet kan vi lägga till L2-regularisering (eftersom matrisen redan är gles behöver vi inte L1-regularisering här)i förlustfunktionen, så kommer den nya ekvationen för förlustfunktionen att vara:

återigen kan vi hitta gradient på uppdaterad MSE och få uppdaterade punkter genom att följa samma tillvägagångssätt som diskuterats ovan

en viktig sak att tänka på i ovanstående scenario matrisen p och q är icke-negativa, varför dessa typer av faktorisering kallas också icke-negativ faktorisering. Som icke-negativ faktorisering extraherar automatiskt information för icke-negativ uppsättning vektor. NMF används ofta i bildbehandling, textutvinning, analys av högdimensionella data