Tim Sort werd voor het eerst geïmplementeerd in 2002 door Tim Peters voor gebruik in Python. Het kwam naar verluidt uit het begrip dat de meeste sorteeralgoritmen worden geboren in klaslokalen, en niet ontworpen voor praktisch gebruik op echte wereld data. Tim Sort maakt gebruik van gemeenschappelijke patronen in data, en maakt gebruik van een combinatie van Merge Sort en Insertion Sort samen met een aantal interne logica om de manipulatie van grootschalige data te optimaliseren.

Waarom Tim Sorteren?

als we naar figuur 2 Kijken, zien we meteen iets interessants. Op zijn best presteert Tim Sort beter dan Merge Sort en Quick Sort. Op zijn slechtst, het draait op vergelijkbare snelheid Merge Sort en eigenlijk overtreft Quick Sort. Met andere woorden, het is onverwacht snel.

in termen van ruimte, Tim Sort is aan de slechtste kant van het spectrum, maar de ruimte overweging voor de meeste sorteeralgoritmen is vrij schaars. O (n) is niet te ruw in de meeste gevallen; het is vermeldenswaard als een mogelijke tekortkoming, en de enige plaats waar Quick Sort echt overtreft Tim Sort.

Het Laatste item waarop sorteeralgoritmen vaak worden beoordeeld is stabiliteit. Stabiliteit is het concept dat, wanneer gesorteerd, objecten van gelijke waarde hun oorspronkelijke volgorde behouden. Je vraagt je misschien af waarom we daar om geven. De artikelen zijn van gelijke waarde-waarom vinden we het erg hoe ze worden besteld?

het eenvoudige antwoord is dat stabiliteit belangrijk is voor gestapelde soorten. Dat wil zeggen, je sorteert eerst op basis van één criteria, dan op basis van een tweede. Als u dit doet in een onstabiel algoritme, verliest u onmiddellijk enige betrouwbaarheid van uw eerste soort wanneer u de tweede uitvoert. Ter referentie: snelle sortering is onstabiel en samenvoegen is stabiel.

Tim Sort is ook stabiel, niet te vergeten snel als licht zwaargewicht (in vergelijking met alleen snel Sorteren). Terwijl sorteeralgoritmen kunnen (en moeten) worden beoordeeld op andere overwegingen, zijn dit de grote drie.

de implementatie in drie stappen

Tim Sort is complex, zelfs door algoritmische standaarden. De uitvoering kan het best worden opgesplitst in onderdelen.

binair zoeken

Het eerste wat je nodig hebt om een Tim Sort te implementeren is een binaire zoekmethode. Dit wordt alleen gebruikt om uw invoegen Sort later te implementeren.

voor referentie: binaire zoekalgoritmen

Insertion Sort & Merge Sort

ten tweede moet u Insertion Sort coderen en Sort samenvoegen. Dit zijn bekende algoritmen, en zouden in de achterzak van de meeste ingenieurs moeten zitten, maar we zullen de basisprincipes bespreken van hoe ze werken en waarom ze waardevol zijn voor ons hier.

Insertion Sort is een zeer eenvoudige sorteer-algoritme. Het loopt door de array, en wanneer het een item tegenkomt dat niet in orde is (strikt minder/meer dan het item ervoor), verplaatst het het naar de juiste positie in de reeds gesorteerde array. Insertion Sort is berucht voor het zeer snel werken op reeds gesorteerde arrays, evenals kleinere arrays. In feite, kunnen we zien uit Fig 2 dat invoegen Sort heeft een indrukwekkende best case looptijd van O(n). Houd in gedachten vooruit te gaan met Tim Sort: het beste geval voor Insertion Sort is een reeds gesorteerde array. Het klinkt misschien gek, maar dat is relevant.

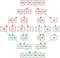
merge sort werkt daarentegen volgens een basisprincipe: het is buitengewoon eenvoudig om reeds gesorteerde arrays samen te voegen. Dus, het splitst een beginnende array in tweeën keer op keer totdat het niets anders is dan enkele elementen. Vervolgens herbouwt het langzaam de hoofdarray door die elementen weer samen te voegen in gesorteerde volgorde. Omdat we begonnen met bouwstenen van grootte één, was het heel gemakkelijk om initiële gesorteerde arrays te bouwen. Dan, het is gemakkelijk om ze samen te voegen. Uiteindelijk besteden we O(n log n) tijd, en (belangrijk) doen we dat op een manier die gegarandeerd stabiel is.

bijvoorbeeld implementaties zie:

samenvoegen Sorteer: https://www.geeksforgeeks.org/merge-sort/

Invoegsorteer: https://www.geeksforgeeks.org/insertion-sort/

implementeer Tim Sort

De sleutel tot het begrijpen van Tim Sort is het gebruik van runs begrijpen. Tim Sort maakt gebruik van natuurlijk voorkomende voorgesorteerde gegevens in zijn voordeel. Met voorgesorteerd bedoelen we simpelweg dat sequentiële elementen allemaal toenemen of afnemen (het maakt ons niet uit welke).

eerst stellen we een minrun grootte in. Wat we hiermee bedoelen is dat we ervoor willen zorgen dat al onze runs op zijn minst een bepaalde lengte hebben. Houd er rekening mee dat we niet garanderen dat we runs van deze omvang zullen vinden — we komen hier later op in. We zeggen gewoon dat een run op zijn minst van een bepaalde lengte moet zijn.

wanneer we een run tegenkomen, zetten we die opzij. Wanneer we de langste run vinden binnen een minrun bereik. We hebben nu een bekende datastructuur: een kleine, gesorteerde array. Als het ten minste minrun in lengte is, dan huzzah! We kunnen verder. Zo niet, dan zetten we Insertion Sort in het spel.

u herinnert zich misschien van bovenaf dat Invoegsortage bijzonder effectief is op twee soorten arrays: kleine en reeds gesorteerde arrays. Wat we net hebben gemaakt is een kleine, gesorteerde reeks. Als het niet ten minste minrun in lengte is, reiken we vooruit en pakken we genoeg andere elementen om de run te voltooien, gebruik dan Insertion Sort om ze snel en eenvoudig in onze gesorteerde array te duwen. Uiteraard, als een run het einde van de array tegenkomt kun je het een beetje kort laten zijn.

zodra je al je runs hebt aangemaakt (dat wil zeggen gesorteerde subarrays), gebruik je je Merge Sort om ze samen te voegen. In het beste geval is de hele array al gesorteerd en Tim Sort is slim genoeg om te weten dat het niets anders hoeft te doen. Andere keren, het heeft de neiging om gewoon zeer efficiënt te zijn. Als extra voordeel zijn zowel Insertion Sort als Merge Sort stabiel, dus de resulterende array is stabiel.

voor degenen die de voorkeur geven aan opsommingstekens:

1. Bepaal een minrun grootte die een macht van 2 is (meestal 32, nooit meer dan 64 of uw Invoegsort zal efficiëntie verliezen)
2. zoek een run in de eerste minrun van gegevens.
3. als de run niet ten minste minrun in lengte is, gebruik dan Insertion Sort om volgende of eerdere items te pakken en ze in de run in te voegen totdat het de juiste minimumgrootte is.
4. herhaal totdat de gehele array is verdeeld in gesorteerde subsecties.
5. gebruik de tweede helft van Merge Sort om de geordende arrays aan te sluiten.

conclusie

Tim Sort is krachtig. Het is snel en stabiel, maar misschien wel het allerbelangrijkste het maakt gebruik van echte wereld patronen en gebruikt ze om een eindproduct te bouwen. Is het voor elke situatie? Waarschijnlijk niet. Veel succes met het programmeren op een whiteboard tijdens een interview, en als je gewoon een snel eenvoudig sorteeralgoritme nodig hebt in een snuifje wil je waarschijnlijk niet de moeite nemen om zoiets complex te implementeren. Echter, voor data wetenschappers kraken nummers is het meer dan de moeite waard een kijkje.

voor de nieuwsgierigen kun je de volledige Tim sorteercode op github bekijken.

bedankt

Dank u allen aan mijn lezers. Ik waardeer uw tijd,en hoop oprecht dat u de inhoud informatief gevonden. Als u vragen of antwoorden hebt, kunt u er hieronder een laten vallen.