V éře digitálního světa, vidíme, doporučení v každé oblasti, počasí je e-commerce webové stránky nebo zábavy webové stránky nebo sociální sítě. Doporučení dává uživateli nejen doporučenou volbu (na základě minulé aktivity), ale také vypráví o chování uživatele (sentimentální analýza nebo emoční AI).

takže nejprve pochopíme, jaké doporučení je. Je to v podstatě doporučuje položku pro uživatele na základě jeho minulé vyhledávání / aktivity.

Obrázek 1 říká, Amazon doporučení na základě předchozí historie prohlížení a posledních vyhledávání. Můžeme tedy říci, že doporučení v podstatě předpovídá budoucí chování založené na minulém chování. K dispozici jsou dva typy přístupů, které se používá v doporučení systému,

1 – Obsah Filtrování Založené na

2 – Kolaborativní filtrování založené na

Obsah Založený Filtrování-

je založena na myšlence, že navrhnu bod na uživatelské K, který je podobný předchozí položku vysoce hodnocen. K. Základní pojetí v obsahu na základě filtrování je TF-IDF (Term frequency — inverse document frequency), který se používá k určení významu dokumentu/slovo/film atd. Na základě obsahu filtrování ukazuje transparentnosti v doporučení, ale na rozdíl od kolaborativního filtrování je možné, aby efektivně pracovat pro velké datové

Kolaborativní filtrování založené na

je založena na myšlence, že lidé, kteří sdílejí stejný zájem na určitý druh položky bude také sdílejí stejný zájem nějaký jiný druh zboží, na rozdíl od obsahu, na základě, které v podstatě spoléhají na metadata, zatímco se zabývá reálném životě aktivity. Tento typ filtrování je flexibilní, aby většina z domény (nebo můžeme říci, že je doména zdarma), ale protože při studeném startu problém řídkosti dat (která byla zpracována matice faktorizace) tento typ algoritmu čelí některé nezdar v nějaké situaci.

Matice faktorizace

Matice faktorizace přichází na výsluní poté, co Netflix soutěže (2006), když Netflix oznámila prize money 1 milion dolarů pro ty, kteří zlepší jeho střední kvadratická výkon o 10%. Netflix za předpokladu, školení sada dat 100,480,507 hodnocení, které 480,189 uživatelům dal 17,770 filmy.

maticová faktorizace je kolaborativní filtrační metoda, kde se matice m * n rozkládá na m * K A K * n. V podstatě se používá pro výpočet složité maticové operace. Rozdělení matice je takové, že pokud vynásobíme faktorizovanou matici, dostaneme původní matici, jak je znázorněno na obrázku 2. Používá se pro zjištění latentní funkce mezi dvě osoby (může být použit pro více než dvě osoby, ale to přijde pod tenzor faktorizace)

Matice rozkladu mohou být klasifikovány do tří typu-

1 – LU rozkladu — Rozkladu matice do L a U je matice, kde L je dolní trojúhelníková matice a U je horní trojúhelníková matice, obecně používá pro zjištění koeficientu lineární regrese. Tento rozklad nepodařilo-li matice nemůže mít snadno rozloží

2 – QR matice rozkladu – Rozkladu matice do Q a R, kde Q je čtvercová matice a R je horní trojúhelníková matice (není nutné, náměstí). Používá se pro analýzu systému eigen

3-Choleskyho rozklad-jedná se o nejčastěji používaný rozklad ve strojovém učení. Používá se pro výpočet lineárního nejmenšího čtverce pro lineární regresi

maticová faktorizace může být použita v různých doménách, jako je rozpoznávání obrazu, doporučení. Matice použitá v tomto typu problému jsou obecně řídké, protože existuje šance, že jeden uživatel může hodnotit pouze některé filmy. Existují různé aplikace pro maticové faktorizace jako redukci Dimenzionality (vědět více o snížení počtu rozměrů naleznete Prokletí Dimenzionality), latentní hodnotu rozkladu,

prohlášení

V Tabulce 1 máme 5 uživatelů a 6 filmů, kde každý uživatel může hodnotit každý film. Jak vidíme, Henry nehodnotil pro Thora a Rocky podobně Jerry nehodnotil pro Avatar. V reálném světě scénář tyto typy matrice může být velmi řídké matice,

Náš problém prohlášení je, že musíme zjistit, pro hodnocení nehodnocené filmy, jak je znázorněno v Tabulce 1,

naším cílem je najít hodnocení uživatele pomocí maticové faktorizace ale předtím, než že musíme jít přes Singulární Rozklad (SVD), protože matice faktorizace a SVD jsou spojeny k sobě navzájem,

SVD a maticová faktorizace

před vstupem do hloubky SVD umožňuje nejprve pochopit, co je K a transponovat(K). Pokud provedeme PCA na matici K (Tabulka 1), dostaneme veškerý uživatelský vektor. Později můžeme dát tyto vektory do sloupců matice U, a pokud budeme plnit DOHODY o provedení(K) dostaneme všechny filmové vektor, který se stal sloupce matice M.

Takže místo provádění PCA na K a transpozice(K) samostatně, můžeme využít SVD, které mohou provádět PCA na K a provedení(K) v jediném záběru. SVD je v podstatě faktorizovaná matice k do matice U, matice M a diagonální matice:

, kde K je Původní Matice, U je uživatel matrix,M je film matrix a prostřední je diagonální matice

Pro jednoduchost, můžeme odstranit diagonální matice na chvíli, takže nová rovnice bude:

Nechť r je rating definován pro uživatele u a položky i, p je řada M pro uživatele a q je sloupec provedení(U) pro konkrétní položky jsem. Takže rovnice bude stát:

Poznámka: — Pokud K je hustá matice hodnoty než M bude vlastní vektor z K*provedení(K), stejně tak hodnota U bude vlastní vektor z transpozice(K)*K, ale naše matice je řídká matice nemůžeme spočítat, U a M, které tento přístup

Tak tady je naším úkolem najít matici M a U . Jedním ze způsobů je inicializovat náhodnou hodnotu na M A U a porovnat ji s původní maticí K, pokud je hodnota blízká K, než zastavit postup jinak minimalizujte hodnotu U A M, dokud nejsou blízko K . Proces těchto typ optimalizace se nazývá gradient klesání,

naším základním úkolem je, aby se minimalizovalo střední kvadratická chybová funkce, která může být reprezentován jako :

As our main task is to minimize the error i.e. musíme zjistit, kterým směrem máme jít, že musíme rozlišovat to, proto nová rovnice bude

Proto aktualizované hodnoty pro p a u bude nyní stát:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Na základě tohoto rozhodnutí řádku můžeme schopen rozlišovat distribuci dat

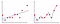
Na Obrázku 2 první obrázek je místo, kde model je vybaven lineárně, zatímco v druhém pozemku je vybavena polynom stupně. Na první pohled to vypadá, že druhý graf je mnohem lepší než první plot, protože dává 99% přesnost tréninkových dat, ale co když zavedeme testovací data a poskytne 50% přesnost testovacích dat. Tento typ problému se nazývá overfitting a k překonání tohoto problému zavádíme koncept nazvaný regularizace.

Jako overfitting problém je běžné v strojového učení tak, tam jsou dva typy regularizace přístup, který může být použit k odstranění overfitting

1 – L1 regularizace

2 – L2 regularizace

L1 regularizace přidat lineární rozsah koeficient jako trest horizontu, zatímco v L2 to přidat metr velikost koeficient pro ztrátu funkce/chyby funkci (jak je popsáno výše). L1 vrací řídké matice, zatímco L2 ne. L1 regularizace funguje dobře při výběru funkcí v řídké matici.

v datovém souboru doporučení jsou také vysoké šance na nadměrné vybavení dat. Tak, aby odstranit overfitting problém můžeme přidat L2 regularizace (jako matrix je již řídké nepotřebujeme L1 regularizace zde)ztráta funkce tedy nové rovnice ztráty funkce bude:

Opět můžeme najít přechodu na aktualizované MSE a získat aktualizované body podle následujících stejný přístup, jak je popsáno výše.

Jednu důležitou věc je třeba zvážit při výše uvedený scénář matice P a Q jsou non-negativní, a proto tyto typy faktorizace je také nazýván non-negativní rozklad. Jako non-negativní faktorizace automaticky extrahuje informace pro non-negativní množinu vektoru. NMF je široce používán při zpracování obrazu, dolování textu, analýze vysokých rozměrových dat