Im Zeitalter der digitalen Welt sehen wir Empfehlungen in jedem Bereich, ob es sich um E-Commerce-Websites, Unterhaltungswebsites oder Websites sozialer Netzwerke handelt. Empfehlung gibt dem Benutzer nicht nur die empfohlene Auswahl (basierend auf früheren Aktivitäten), sondern auch Informationen zum Benutzerverhalten (sentimentale Analyse oder Emotionserkennung).

Also lasst uns zuerst verstehen, was Empfehlung ist. Grundsätzlich empfiehlt es dem Benutzer ein Element basierend auf seiner früheren Suche / Aktivität.

Abbildung 1 zeigt die Empfehlung von Amazon basierend auf dem bisherigen Browserverlauf und den vergangenen Suchvorgängen an. Wir können also sagen, dass Empfehlung im Grunde genommen zukünftiges Verhalten basierend auf vergangenem Verhalten vorhersagt. Es gibt zwei Arten von Ansätzen, die im Empfehlungssystem verwendet werden

1- Inhaltsbasierte Filterung

2- Inhaltsbasierte Filterung

Inhaltsbasierte Filterung-

Es basiert auf der Idee, den Artikel dem Benutzer K zu empfehlen, der dem vorherigen Artikel ähnelt, der von K hoch bewertet wurde. Inhaltsbasierte Filterung zeigt Transparenz in der Empfehlung, aber im Gegensatz zur kollaborativen Filterung kann sie nicht effizient für große Datenmengen arbeiten

Kollaborative Filterung

Es basiert auf der Idee, dass Menschen, die das gleiche Interesse an bestimmten teilen Art von Gegenständen wird auch das gleiche Interesse an einer anderen Art von Gegenständen teilen, im Gegensatz zu Inhalten, die im Grunde auf Metadaten beruhen, während sie sich mit realen Aktivitäten befassen. Diese Art der Filterung ist für den größten Teil der Domäne flexibel (oder wir können sagen, dass sie domänenfrei ist), aber aufgrund des Kaltstartproblems, der Datensparsamkeit (die durch Matrixfaktorisierung gehandhabt wurde), steht diese Art von Algorithmus in einigen Szenarien vor einem Rückschlag.

Matrixfaktorisierung

Die Matrixfaktorisierung steht nach dem Netflix-Wettbewerb (2006) im Rampenlicht, als Netflix ein Preisgeld von 1 Million US-Dollar für diejenigen ankündigte, die die Leistung des quadratischen Mittelwerts um 10% verbessern werden. Netflix lieferte einen Trainingsdatensatz von 100.480.507 Bewertungen, die 480.189 Benutzer 17.770 Filmen gaben.

Die Matrixfaktorisierung ist die kollaborative Filtermethode, bei der die Matrix m*n in m* k und k* n zerlegt wird. Es wird grundsätzlich zur Berechnung komplexer Matrixoperationen verwendet. Division der Matrix ist so, dass, wenn wir faktorisierte Matrix multiplizieren wir ursprüngliche Matrix erhalten, wie in Abbildung 2 gezeigt. Es wird verwendet, um latente Merkmale zwischen zwei Entitäten zu entdecken (kann für mehr als zwei Entitäten verwendet werden, dies wird jedoch unter Tensorfaktorisierung fallen)

Abbildung 2: Matrixfaktorisierung- Quelle

Die Matrixzerlegung kann in drei Typen eingeteilt werden-

1- LU—Zerlegung – Zerlegung der Matrix in L- und U-Matrix, wobei L die untere Dreiecksmatrix und U die obere Dreiecksmatrix ist, die im Allgemeinen zum Ermitteln des linearen Regressionskoeffizienten verwendet wird. Diese Zerlegung ist fehlgeschlagen, wenn sich die Matrix nicht leicht zersetzen lässt

2- QR-Matrixzerlegung – Zerlegung der Matrix in Q und R, wobei Q eine quadratische Matrix und R eine obere dreieckige Matrix ist (kein notwendiges Quadrat). Wird für die Eigensystemanalyse verwendet

3- Cholesky-Zerlegung – Dies ist die am häufigsten verwendete Zerlegung im maschinellen Lernen. Wird zur Berechnung des linearen kleinsten Quadrats für die lineare Regression verwendet

Die Matrixfaktorisierung kann in verschiedenen Bereichen wie Bilderkennung usw. verwendet werden. Matrix in dieser Art von Problem verwendet werden, sind in der Regel spärlich, weil es Chance, dass ein Benutzer nur einige Filme bewerten könnte. Es gibt verschiedene Anwendungen für die Matrix-Faktorisierung wie Dimensionalitätsreduktion (um mehr über Dimensionalitätsreduktion zu erfahren, siehe Fluch der Dimensionalität), latente Wertzerlegung

Problemstellung

In Tabelle 1 haben wir 5 Benutzer und 6 Filme, in denen jeder Benutzer jeden Film bewerten kann. Wie wir sehen können, hat Henry nicht für Thor und Rocky bewertet, ähnlich wie Jerry nicht für Avatar. Im realen Szenario können diese Matrixtypen sehr spärlich sein Matrix

Unsere Problemstellung ist, dass wir Bewertungen für Filme ohne Bewertung herausfinden müssen, wie in Tabelle 1 gezeigt

Unser Ziel ist es, die Bewertung des Benutzers durch Matrixfaktorisierung zu ermitteln, aber vorher müssen wir die Singularwertzerlegung (SVD) durchlaufen, da Matrixfaktorisierung und SVD miteinander verwandt sind

SVD und Matrixfaktorisierung

Bevor wir in die Tiefe von SVD gehen, sollten wir zuerst verstehen, was K ist und transponieren(K). Wenn wir PCA auf Matrix K (Tabelle 1) durchführen, erhalten wir den gesamten Benutzervektor. Später können wir diese Vektoren in die Spalte der Matrix U einfügen und wenn wir PCA bei der Transponierung (K) ausführen, erhalten wir den gesamten Filmvektor, der zur Spalte für die Matrix M wird.

Anstatt also PCA für K und Transponieren (K) separat auszuführen, können wir SVD verwenden, das PCA für K und Transponieren (K) in einem einzigen Schuss ausführen kann. SVD ist im Grunde faktorisierte Matrix K in Matrix U, Matrix M und Diagonalmatrix:

wo K ist Original Matrix, U ist benutzer matrix,M ist Diagonalmatrix und die mittlere ist Diagonalmatrix

Der Einfachheit halber können wir die Diagonalmatrix für eine Weile entfernen, so dass die neue Gleichung:

p ist die Zeile von M für einen Benutzer und q ist die Spalte von transpose (U) für ein bestimmtes Element i. Die Gleichung wird also:

Hinweis — Wenn K ein dichter Matrixwert ist, ist M der Eigenvektor von K*transpose(K), ebenso der Wert von U der Eigenvektor von transpose(K)*K, aber unsere Matrix ist eine spärliche Matrix, die wir nicht berechnen können U und M durch diesen Ansatz

Hier besteht unsere Aufgabe darin, die Matrix M und U zu finden. Eine Möglichkeit besteht darin, den Zufallswert auf M und U zu initialisieren und ihn mit der ursprünglichen Matrix K zu vergleichen, wenn der Wert nahe bei K liegt, als die Prozedur zu stoppen, andernfalls den Wert von U und M zu minimieren, bis sie nahe bei K liegen. Der Prozess dieser Art der Optimierung wird Gradient descent genannt

Unsere grundlegende Aufgabe besteht also darin, die mittlere quadratische Fehlerfunktion zu minimieren, die als dargestellt werden kann :

As our main task is to minimize the error i.e. wir müssen herausfinden, in welche Richtung wir gehen müssen, um es zu differenzieren, daher wird die neue Gleichung

Daher wird der aktualisierte Wert für p und u jetzt werden:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Basierend auf dieser Entscheidungslinie können wir die Verteilung der Daten unterscheiden

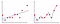
In Abbildung 2 wird das Modell im ersten Diagramm linear angepasst, während es im zweiten Diagramm mit einem Polynomgrad angepasst wird. Auf den ersten Blick sieht es so aus, als wäre der zweite Plot weitaus besser als der erste Plot, da er eine Genauigkeit von 99% bei den Trainingsdaten bietet. Um dieses Problem zu überwinden, führen wir ein Konzept namens Regularisierung ein.

Da das Problem der Überanpassung beim maschinellen Lernen häufig auftritt, gibt es zwei Arten von Regularisierungsansätzen, mit denen die Überanpassung entfernt werden kann

1- L1-Regularisierung

2- L2-Regularisierung

Die L1-Regularisierung addiert die lineare Größe des Koeffizienten als Strafterm, während sie in L2 die quadratische Größe des Koeffizienten zur Verlustfunktion / Fehlerfunktion hinzufügt (wie oben erörtert). L1 gibt spärliche Matrizen zurück, während L2 dies nicht tut. Die L1-Regularisierung funktioniert gut bei der Feature-Auswahl in einer spärlichen Matrix.

Auch im Empfehlungsdatensatz besteht eine hohe Wahrscheinlichkeit einer Überanpassung der Daten. Um das Überanpassungsproblem zu beseitigen, können wir die L2-Regularisierung (da die Matrix bereits spärlich ist, benötigen wir hier keine L1-Regularisierung) in die Verlustfunktion einfügen, daher lautet die neue Gleichung der Verlustfunktion:

Eine wichtige Sache, die im obigen Szenario berücksichtigt werden muss, ist, dass die Matrix P und Q nicht negativ sind, daher werden diese Arten der Faktorisierung auch als nicht negative Faktorisierung bezeichnet. Als nicht-negative Faktorisierung extrahiert automatisch Informationen für nicht-negative Menge von Vektor. NMF ist weit verbreitet in der Bildverarbeitung, Text Mining, Analyse von hochdimensionalen Daten