Definición del proyecto Nayuki
: La secuencia de Fibonacci se define como \(F(0) = 0\), \(F(1) = 1\), y \(F(n) = F(n-1) + F(n-2)\) para \(n ≥ 2\). Así que la secuencia (empezando por \(F (0)\)) es 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
Si queremos calcular un único término en la secuencia (por ejemplo, \(F(n)\)), hay un par de algoritmos para hacerlo. Algunos algoritmos son mucho más rápidos que otros.
Algoritmos
Libro de texto recursivo (extremadamente lento)
Ingenuamente, podemos ejecutar directamente la recurrencia como se indica en la definición matemática de la secuencia de Fibonacci. Desafortunadamente, es irremediablemente lento: Utiliza \(Θ (n)\) espacio de pila y operaciones aritméticas \(Θ(φ^n)\), donde \(φ = \ frac {\sqrt{5} + 1}{2}\) (la proporción áurea). En otras palabras, el número de operaciones para calcular \(F (n)\) es proporcional a la respuesta numérica final, que crece exponencialmente.
Programación dinámica (lenta)
Debería quedar claro que si ya calculamos \(F(k-2)\) y \(F(k-1)\), entonces podemos agregarlos para obtener \(F(k)\). A continuación, agregamos \(F(k-1)\) y \(F(k)\) para obtener \(F(k+1)\). Repetimos hasta llegar a \(k = n\). La mayoría de las personas notan este algoritmo automáticamente, especialmente cuando computan Fibonacci a mano. Este algoritmo toma operaciones de espacio \(Θ(1)\) y \(Θ(n)\).
Exponenciación matricial (rápida)
El algoritmo se basa en esta identidad de aspecto inocente (que se puede probar mediante inducción matemática):
\( \left^n = \left \).
Es importante utilizar la exponenciación por cuadratura con este algoritmo, porque de lo contrario degenera en el algoritmo de programación dinámica. Este algoritmo toma operaciones de espacio \(Θ(1)\) y \(Θ(\log n)\). (Nota: Estamos contando el número de operaciones aritméticas de bigint, no de operaciones de palabras de ancho fijo.)
Duplicación rápida (más rápida)
Dados \(F (k)\) y \(F (k+1)\), podemos calcular estos:
\(\begin{align}F(2k) &= F (k) \left. \\F (2k + 1) &= F(k+1)^2 + F(k)^2.\end{align}\)
Estas identidades se pueden extraer del algoritmo de exponenciación de la matriz. En cierto sentido, este algoritmo es el algoritmo de exponenciación de matriz con los cálculos redundantes eliminados. Debería ser un factor constante más rápido que la exponenciación de la matriz, pero la complejidad temporal asintótica sigue siendo la misma.
Resumen: Los dos algoritmos rápidos de Fibonacci son la exponenciación matricial y la duplicación rápida, cada uno con una complejidad asintótica de operaciones aritméticas \(Θ(\log n)\) bigint. Ambos algoritmos usan multiplicación, por lo que se vuelven aún más rápidos cuando se usa la multiplicación de Karatsuba. Los otros dos algoritmos son lentos; solo usan suma y no multiplicación.
código Fuente
Implementaciones están disponibles en varios idiomas:
-
Java: FastFibonacci.java (los 3 algoritmos, punto de referencia de tiempo, programa principal ejecutable)
-
Python: fastfibonacci.py (solo función de duplicación rápida)
-
Haskell: fastfibonacci.hs (solo función de duplicación rápida)
-
C#: FastFibonacci.cs (solo duplicación rápida, programa principal ejecutable)
(requiere. NET Framework 4.0 o superior; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
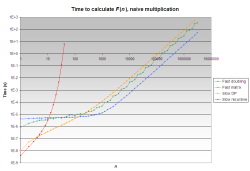
All algorithms, naive multiplication
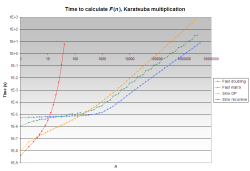
All algorithms, Karatsuba multiplication
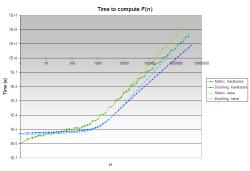
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive |
|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||
| 3 981 072 | 7 654 000 000 |
Todos los tiempos se dan en nanosegundos (ns), dada a 4 cifras significativas. Todas las pruebas anteriores se realizaron en Intel Core 2 Quad Q6600 (2,40 GHz) utilizando un solo hilo, Windows XP SP 3, Java 1.6.0_22.
Pruebas
Exponenciación de matriz
Usaremos inducción débil para probar esta identidad.
Caso base
Para \(n = 1\), claramente \( \left^1 = \left\).
Paso de inducción
Asume para \(n ≥ 1\) que \( \left^n = \left\). Entonces:
\(\left^{n+1} \\= \left^n \left \\= \left \left \\= \left \\= \left.\)
Duplicación rápida
Asumiremos el hecho de que el método de exponenciación de matriz es correcto para todos los \(n ≥ 1\).
\(\left \\= \left^{2n} \\= \left( \left^n \derecho)^2 \\= \left^2 \\= \left.\)
Por lo tanto, al igualar las celdas de la matriz:
\(\begin{align}F(2n+1) &= F(n+1)^2 + F(n)^2. \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)