En la era del mundo digital, vemos recomendaciones en todas las áreas, en sitios web de comercio electrónico, sitios web de entretenimiento o sitios de redes sociales. La recomendación no solo le da al usuario su elección recomendada (basada en la actividad pasada), sino que también le informa sobre el comportamiento del usuario (análisis sentimental o IA emocional).

Primero, entendamos qué es la recomendación. Básicamente, está recomendando el artículo al usuario en función de su búsqueda/actividad pasada.

la Figura 1 indica Amazon recomendación basada en el pasado historial de navegación y las búsquedas anteriores. Por lo tanto, podemos decir que la recomendación es básicamente predecir el comportamiento futuro basado en el comportamiento pasado. Hay dos tipos de enfoques que se utilizan en el sistema de recomendación

1 – Filtrado basado en contenido

2 – Filtrado basado en colaboración

Filtrado basado en contenido-

Se basa en la idea de recomendar el elemento al usuario K, que es similar al elemento anterior altamente calificado por K. El concepto básico en el filtrado basado en contenido es TF-IDF (Frecuencia de término — frecuencia de documento inversa), que se utiliza para determinar la importancia del documento/palabra/película, etc. El filtrado basado en contenido muestra transparencia en la recomendación, pero a diferencia del filtrado colaborativo, no puede funcionar de manera eficiente para datos grandes

El filtrado basado en colaboración

Se basa en la idea de que las personas que comparten el mismo interés en cierto tipo de elementos también compartirán el mismo interés en algún otro tipo de elementos, a diferencia del basado en contenido que básicamente se basa en metadatos mientras se ocupa de la actividad de la vida real. Este tipo de filtrado es flexible para la mayor parte del dominio (o podemos decir que es libre de dominio), pero debido al problema de arranque en frío, la escasez de datos (que se manejó mediante factorización de matrices), este tipo de algoritmo enfrenta algún contratiempo en algún escenario.

Factorización de matrices

La factorización de matrices aparece en primer plano después de la competencia de Netflix (2006), cuando Netflix anunció un premio de 1 millón de dólares a aquellos que mejorarán su rendimiento de cuadratura media raíz en un 10%. Netflix proporcionó un conjunto de datos de entrenamiento de 100,480,507 calificaciones que 480,189 usuarios dieron a 17,770 películas.

La factorización de matrices es el método de filtrado basado en colaboración donde la matriz m * n se descompone en m * k y k * n . Se utiliza básicamente para el cálculo de la operación de matriz compleja. La división de la matriz es tal que si multiplicamos la matriz factorizada obtendremos la matriz original como se muestra en la Figura 2. Se utiliza para descubrir latente características entre dos entidades (puede ser utilizado para más de dos entidades, pero esto vendrá bajo el tensor de factorización)

La descomposición de la matriz se puede clasificar en tres tipos –

Descomposición de 1-LU-Descomposición de la matriz en matriz L y U donde L es la matriz triangular inferior y U es la matriz triangular superior, generalmente utilizada para encontrar el coeficiente de regresión lineal. Esta descomposición falló si la matriz no se pudo descomponer fácilmente

Descomposición de la matriz 2-QR-Descomposición de la matriz en Q y R donde Q es matriz cuadrada y R es matriz triangular superior (no es necesario cuadrado). Utilizado para análisis de sistemas propios

3-Descomposición de Cholesky – Esta es la descomposición más utilizada en el aprendizaje automático. Se utiliza para calcular el mínimo cuadrado lineal para regresión lineal La factorización de matrices se puede usar en varios dominios, como el reconocimiento de imágenes, la recomendación. Las matrices utilizadas en este tipo de problemas son generalmente escasas porque existe la posibilidad de que un usuario califique solo algunas películas. Hay varias aplicaciones para la factorización de matrices, como la reducción de dimensionalidad (para saber más sobre la reducción de dimensionalidad, consulte Maldición de la dimensionalidad), descomposición de valores latentes

Declaración de problemas

En la Tabla 1 tenemos 5 usuarios y 6 películas donde cada usuario puede calificar cualquier película. Como podemos ver, Henry no calificó para Thor y Rocky de manera similar, Jerry no calificó para Avatar. En el escenario del mundo real, estos tipos de matrices pueden ser muy dispersas

Nuestra declaración de problema es que tenemos que encontrar clasificaciones para películas no clasificadas como se muestra en la Tabla 1

Como nuestro objetivo es encontrar la calificación del usuario por factorización de matrices, pero antes de eso tenemos que pasar por la Descomposición de Valores Singulares (SVD) porque la factorización de matrices y SVD están relacionadas entre sí

SVD y factorización de matrices

Antes de ir a la profundidad de SVD, primero entendamos qué es K y transponer (K). Si realizamos PCA en la matriz K (Tabla 1) obtenemos todo el vector de usuario. Más tarde podemos poner estos vectores en la columna de la matriz U y si realizamos PCA en la transposición(K) obtenemos todo el vector de película que se convierte en columna para la matriz M.

Así que en lugar de realizar PCA en K y transponer(K) por separado, podemos usar SVD que puede realizar PCA en K y transponer(K) en una sola toma. SVD es básicamente matriz factorizada K en matriz U, matriz M y matriz diagonal:

donde K es Matriz original, U es matriz de usuario,M es matriz de película y la del medio es matriz diagonal

En aras de la simplicidad, podemos eliminar la matriz diagonal por un tiempo para que la nueva ecuación se convierta en:

Deje que r es de clasificación definido por el usuario u y el artículo i, p es la fila de M para un usuario y q es la columna de la transposición(U) para un elemento específico que yo. Así que la ecuación se convertirá en:

tenga en cuenta — Si K es la matriz densa valor de M será autovector de K*transpose(K), de modo similar, el valor de U se autovector de transponer(K)*K pero nuestra matriz es la matriz dispersa, no podemos calcular U y M por este enfoque

Así que aquí nuestra tarea es encontrar la matriz M y U . Una forma es inicializar el valor aleatorio a M y U y compararlo con la matriz original K si el valor está cerca de K que detener el procedimiento de lo contrario minimizar el valor de U y M hasta que estén cerca de K . El proceso de este tipo de optimización se llama gradiente de descenso

Así que nuestra tarea es la de minimizar el error cuadrático medio de la función que puede ser representada como :

As our main task is to minimize the error i.e. tenemos que encontrar la dirección en la que tenemos que ir por que tenemos que diferenciar es, por lo tanto la nueva ecuación se convertirá

por lo tanto el valor actualizado de p y u será convertido en:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . En base a esa línea de decisión, podemos distinguir la distribución de datos

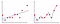
En la Figura 2, la primera gráfica es donde el modelo se ajusta linealmente, mientras que en la segunda gráfica se ajusta con grado polinómico. A primera vista, parece que la segunda gráfica es mucho mejor que la primera gráfica, ya que proporciona un 99% de precisión en los datos de entrenamiento, pero qué pasa si introducimos datos de prueba y da un 50% de precisión en los datos de prueba . Este tipo de problema se llama sobreajuste y para superar este problema introducimos un concepto llamado regularización.

Como el problema de sobreajuste es común en el aprendizaje automático, hay dos tipos de enfoque de regularización que se pueden usar para eliminar el sobreajuste

regularización 1 – L1

regularización 2 – L2

La regularización L1 agrega magnitud lineal de coeficiente como término de penalización, mientras que en L2 agrega magnitud cuadrada de coeficiente a la función de pérdida/función de error (como se discutió anteriormente). L1 devuelve matrices dispersas, mientras que L2 no lo hace. La regularización L1 funciona bien en la selección de características en matriz dispersa.

En el conjunto de datos de recomendación también hay altas posibilidades de sobreajustar los datos. Por lo tanto, para eliminar el problema de sobreajuste, podemos agregar la regularización L2 (como la matriz ya es escasa, no necesitamos la regularización L1 aquí) en la función de pérdida, por lo tanto, la nueva ecuación de la función de pérdida será:

Nuevamente podemos encontrar gradiente en MSE actualizado y obtener puntos actualizados siguiendo el mismo enfoque que se discutió anteriormente

Una cosa importante a tener en cuenta en el escenario anterior, la matriz P y Q no son negativas, por lo que estos tipos de factorización también se denominan factorización no negativa. Como la factorización no negativa extrae automáticamente información para el conjunto de vectores no negativos. NMF es ampliamente utilizado en el procesamiento de imágenes ,minería de texto, análisis de datos de alta dimensión