À l’ère du monde numérique, nous voyons des recommandations dans tous les domaines, qu’il s’agisse de sites de commerce électronique ou de sites de divertissement ou de sites de réseaux sociaux. La recommandation donne non seulement à l’utilisateur son choix recommandé (basé sur l’activité passée) mais elle parle également du comportement de l’utilisateur (analyse sentimentale ou IA émotionnelle).

Alors d’abord, comprenons ce qu’est une recommandation. Il recommande essentiellement l’élément à l’utilisateur en fonction de sa recherche / activité passée.

La figure 1 indique la recommandation d’Amazon en fonction de l’historique de navigation passé et des recherches passées. Nous pouvons donc dire que la recommandation consiste essentiellement à prédire le comportement futur en fonction du comportement passé. Il existe deux types d’approches utilisées dans le système de recommandation

1- Filtrage basé sur le contenu

2- Filtrage basé sur la collaboration

Filtrage basé sur le contenu –

Il est basé sur l’idée de recommander l’élément à l’utilisateur K, ce qui est similaire à l’élément précédent hautement noté par K. Le concept de base du filtrage basé sur le contenu est TF-IDF (Terme fréquence — fréquence de document inverse), qui est utilisé pour déterminer l’importance du document / mot / film, etc. Le filtrage basé sur le contenu montre une transparence dans la recommandation, mais contrairement au filtrage collaboratif, il ne peut pas fonctionner efficacement pour des données volumineuses

Filtrage basé sur la collaboration

Il est basé sur l’idée que les personnes qui partagent le même intérêt pour certains types d’éléments partageront également le même intérêt pour d’autres types d’éléments contrairement au contenu basé sur des métadonnées qui s’appuient essentiellement sur des métadonnées alors qu’il traite de l’activité réelle. Ce type de filtrage est flexible pour la plupart du domaine (ou on peut dire qu’il est libre de domaine) mais en raison d’un problème de démarrage à froid, la rareté des données (qui a été gérée par factorisation matricielle) ce type d’algorithme fait face à un certain recul dans certains scénarios.

La factorisation matricielle

La factorisation matricielle apparaît sous les projecteurs après la concurrence de Netflix (2006) lorsque Netflix a annoncé un prix de 1 million de dollars à ceux qui amélioreront ses performances quadratiques moyennes de 10%. Netflix a fourni un ensemble de données de formation de 100 480 507 notes attribuées par 480 189 utilisateurs à 17 770 films.

La factorisation matricielle est la méthode de filtrage basée sur la collaboration où la matrice m*n est décomposée en m *k et k *n. Il est essentiellement utilisé pour le calcul de l’opération matricielle complexe. La division de la matrice est telle que si nous multiplions la matrice factorisée, nous obtiendrons la matrice d’origine comme le montre la figure 2. Il est utilisé pour découvrir des entités latentes entre deux entités (peut être utilisé pour plus de deux entités mais cela fera l’objet d’une factorisation tensorielle)

La décomposition matricielle peut être classée en trois types –

1-Décomposition LU — Décomposition de la matrice en matrice L et U où L est la matrice triangulaire inférieure et U est la matrice triangulaire supérieure, généralement utilisée pour trouver le coefficient de régression linéaire. Cette décomposition a échoué si la matrice ne peut pas se décomposer facilement

2 – Décomposition de la matrice QR – Décomposition de la matrice en Q et R où Q est une matrice carrée et R est une matrice triangulaire supérieure (carré non nécessaire). Utilisé pour l’analyse du système propre

3 – Décomposition de Cholesky – C’est la décomposition la plus utilisée dans l’apprentissage automatique. Utilisé pour le calcul des moindres carrés linéaires pour la régression linéaire

La factorisation matricielle peut être utilisée dans divers domaines tels que la reconnaissance d’images, la recommandation. Les matrices utilisées dans ce type de problème sont généralement rares car il est possible qu’un utilisateur ne note que certains films. Il existe diverses applications pour la factorisation matricielle telles que la réduction de la dimensionnalité (pour en savoir plus sur la réduction de la dimensionnalité, veuillez vous référer à La Malédiction de la dimensionnalité), la décomposition en valeurs latentes

Énoncé du problème

Dans le tableau 1, nous avons 5 utilisateurs et 6 films où chaque utilisateur peut évaluer n’importe quel film. Comme nous pouvons le voir, Henry n’a pas évalué pour Thor et Rocky de même, Jerry n’a pas évalué pour Avatar. Dans un scénario réel, ces types de matrice peuvent être une matrice très clairsemée

Notre énoncé de problème est que nous devons trouver des notes pour les films non classés comme indiqué dans le tableau 1

Notre objectif est de trouver la notation de l’utilisateur par factorisation matricielle, mais avant cela, nous devons passer par une décomposition en valeurs singulières (SVD) car la factorisation matricielle et la SVD sont liées l’une à l’autre p>

La factorisation SVD et matricielle

Avant d’aller à la profondeur de SVD permet d’abord de comprendre ce qu’est K et de transposer (K). Si nous effectuons PCA sur la matrice K (tableau 1), nous obtenons tout le vecteur utilisateur. Plus tard, nous pouvons mettre ces vecteurs dans la colonne de la matrice U et si nous effectuons PCA sur la transposition (K), nous obtenons tous les vecteurs de film qui deviennent colonne pour la matrice M.

Donc, au lieu d’effectuer PCA sur K et transposer (K) séparément, nous pouvons utiliser SVD qui peut effectuer PCA sur K et transposer (K) en un seul plan. SVD est essentiellement une matrice factorisée K en matrice U, matrice M et matrice diagonale:

où K est la matrice d’origine, U est la matrice d’utilisateur, M est la matrice de film et celle du milieu est la matrice diagonale

Par souci de simplicité, nous pouvons supprimer la matrice diagonale pendant un certain temps afin que la nouvelle équation devienne:

Soit r est la notation définie pour l’utilisateur u et l’élément i, p est la ligne de M pour un utilisateur et q est la colonne de transposition (U) pour un élément spécifique i. Donc l’équation deviendra:

Remarque — Si K est une valeur de matrice dense que M sera vecteur propre de K * transpose(K), de même la valeur de U sera vecteur propre de transpose(K) *K mais notre matrice est une matrice clairsemée, nous ne pouvons pas calculer U et M par cette approche

Donc ici notre tâche est pour trouver la matrice M et U. Une façon consiste à initialiser la valeur aléatoire sur M et U et à la comparer avec la matrice d’origine K si la valeur est proche de K, alors arrêtez la procédure sinon minimisez la valeur de U et M jusqu’à ce qu’ils soient proches de K. Le processus de ce type d’optimisation est appelé descente de gradient

Notre tâche de base est donc de minimiser la fonction d’erreur quadratique moyenne qui peut être représentée comme :

As our main task is to minimize the error i.e. nous devons trouver dans quelle direction nous devons aller pour cela nous devons le différencier, par conséquent la nouvelle équation deviendra

Par conséquent, la valeur mise à jour pour p et u sera maintenant devenue:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Sur la base de cette ligne de décision, nous pouvons distinguer la distribution des données

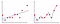
Dans la figure 2, le premier tracé est l’endroit où le modèle est ajusté linéairement tandis que dans le second tracé, il est équipé d’un degré polynomial. À première vue, il semble que le deuxième tracé soit bien meilleur que le premier car il donne une précision de 99% sur les données d’entraînement, mais que se passe-t-il si nous introduisons des données de test et que cela donne une précision de 50% sur les données de test. Ce type de problème est appelé surajustement et pour surmonter ce problème, nous introduisons un concept appelé régularisation.

Comme le problème de surajustement est courant dans l’apprentissage automatique, il existe deux types d’approche de régularisation qui peuvent être utilisés pour supprimer le surajustement

régularisation 1-L1

régularisation 2-L2

La régularisation L1 ajoute une magnitude linéaire du coefficient comme terme de pénalité tandis que dans L2, elle ajoute une magnitude carrée du coefficient à la fonction de perte / fonction d’erreur (comme discuté ci-dessus). L1 renvoie des matrices clairsemées alors que L2 ne le fait pas. La régularisation L1 fonctionne bien dans la sélection des entités dans une matrice clairsemée.

Dans l’ensemble de données de recommandation également, il y a de fortes chances de surajustement des données. Donc, pour supprimer le problème de surajustement, nous pouvons ajouter la régularisation L2 (comme la matrice est déjà clairsemée, nous n’avons pas besoin de régularisation L1 ici) dans la fonction de perte, donc une nouvelle équation de la fonction de perte sera:

Encore une fois, nous pouvons trouver un gradient sur MSE mis à jour et obtenir des points mis à jour en suivant la même approche que celle décrite ci-dessus

Une chose importante à considérer dans le scénario ci-dessus, la matrice P et Q sont non négatives, d’où ces types de factorisation sont également appelés factorisation non négative. Comme la factorisation non négative extrait automatiquement les informations pour un ensemble de vecteurs non négatif. NMF est largement utilisé dans le traitement d’images, l’exploration de texte, l’analyse de données dimensionnelles élevées