a digitális világ korában minden területen ajánlást látunk időjárás ez az e-kereskedelmi webhely vagy szórakoztató webhely vagy közösségi hálózati oldalak. Az ajánlás nemcsak a felhasználó által ajánlott választást adja (a múltbeli tevékenység alapján), hanem a felhasználói viselkedésről is szól (szentimentális elemzés vagy érzelem AI).

tehát először értsük meg, mi az ajánlás. Ez alapvetően ajánlja elem felhasználó alapján a korábbi keresési / tevékenység.

az 1. ábra az Amazon ajánlását mutatja a múltbeli böngészési előzmények és a korábbi keresések alapján. Tehát azt mondhatjuk, hogy az ajánlás alapvetően a jövőbeli viselkedés előrejelzését jelenti a múltbeli viselkedés alapján. Kétféle megközelítés létezik, amelyet az ajánlási rendszerben használnak

1-Tartalom alapú szűrés

2-kollaboratív alapú szűrés

tartalom alapú szűrés-

Ez azon az ötleten alapul, hogy az elemet a K felhasználónak ajánlják, amely hasonló a k által nagyra értékelt előző elemhez.a tartalom alapú szűrés alapkoncepciója a TF — IDF (kifejezés frekvencia-inverz dokumentumfrekvencia), amelyet a dokumentum/szó/film stb. A tartalom alapú szűrés átláthatóságot mutat az ajánlásokban, de az együttműködő szűréssel ellentétben nem képes hatékonyan működni a nagy adatoknál

kollaboratív alapú szűrés

azon az elképzelésen alapul, hogy az emberek, akik azonos érdeklődést mutatnak bizonyos típusú elemek iránt, ugyanolyan érdeklődést mutatnak más típusú elemek iránt is, ellentétben a tartalommal, amely alapvetően metaadatokra támaszkodik, miközben a valós tevékenységekkel foglalkozik. Ez a fajta szűrés rugalmas, hogy a legtöbb domain (vagy azt mondhatjuk, hogy a domain ingyenes), hanem azért, mert a hidegindítás probléma, adatok ritkaság (amely által kezelt mátrix faktorizálás) az ilyen típusú algoritmus arcok némi visszaesés bizonyos forgatókönyv.

Mátrixfaktorizálás

a Mátrixfaktorizálás a Netflix verseny (2006) után kerül reflektorfénybe, amikor a Netflix 1 millió dolláros nyereményt hirdetett azoknak, akik 10% – kal javítják a gyökér átlag négyzet teljesítményét. A Netflix 100 480 507 értékelésből álló képzési adatkészletet nyújtott be, amelyet 480 189 felhasználó adott 17 770 filmhez.

a Mátrixfaktorizálás az együttműködésen alapuló szűrési módszer, ahol az m*N mátrixot m*k-ra és k*n-re bontják . Ez alapvetően kiszámításához használt komplex mátrix működését. A mátrix felosztása olyan, hogy ha megszorozzuk a faktorizált mátrixot, akkor az eredeti mátrixot kapjuk, amint az a 2. ábrán látható. Két entitás közötti látens funkciók felfedezésére szolgál (kettőnél több entitásnál használható, de ez tenzor faktorizálás alá kerül)

a Mátrix bomlása három típusba sorolható-

1 – LU bomlás — a mátrix bomlása L és U mátrixba, ahol L alsó háromszög mátrix és U felső háromszög mátrix, általában a lineáris regresszió együtthatójának meghatározására használják. Ez a bomlás meghiúsult, ha a mátrix nem bomlik le könnyen

2 – QR mátrix bomlás – a mátrix bomlása Q-ra és R-re, ahol Q négyzetmátrix és R felső háromszögmátrix (nem szükséges négyzet). Használt eigen rendszer elemzés

3-Cholesky bomlás-ez a leggyakrabban használt bomlás a gépi tanulásban. Kiszámításához használt lineáris legkisebb négyzet lineáris regresszió

mátrix faktorizálás lehet használni a különböző tartományban, mint a képfelismerés, ajánlás. Az ilyen típusú problémákban használt mátrix általában ritka, mert van esély arra, hogy egy felhasználó csak néhány filmet értékeljen. Vannak különböző alkalmazások mátrix faktorizálás, mint a dimenzió redukció (többet tudni dimenzió redukció lásd Curse of Dimensionality), látens érték bomlás

probléma nyilatkozat

az 1.táblázatban van 5 felhasználó és 6 film, ahol minden felhasználó értékelheti bármilyen filmet. Mint láthatjuk, Henry nem értékelte Thort, Rocky pedig Jerry nem értékelte az Avatart. A valós világban az ilyen típusú mátrixok Nagyon ritka mátrixok lehetnek

problémánk az, hogy meg kell találnunk a nem minősített filmek értékelését az 1. táblázat szerint

mint célunk, hogy megtaláljuk a felhasználó besorolását mátrixfaktorizálás alapján, de előtte át kell esnünk a szinguláris értékbontáson (SVD), mert a mátrixfaktorizálás és az SVD összefügg egymással

SVD és mátrix faktorizálás

mielőtt az SVD mélységébe lépnénk, először értsük meg, mi az A K és ültessük át a(K) – t. Ha PCA-t hajtunk végre a K mátrixon(1.táblázat), megkapjuk az összes felhasználói vektort. Később ezeket a vektorokat az U mátrix oszlopába helyezhetjük, és ha PCA-t hajtunk végre a transpose(K) – ON, akkor megkapjuk az összes filmvektort, amely az M mátrix oszlopává válik. SVD alapvetően faktorizált mátrix K A mátrix U, mátrix M és átlós mátrix:

ahol k az eredeti mátrix, u a felhasználói mátrix,m a filmmátrix, a középső pedig az átlós mátrix

az egyszerűség kedvéért egy ideig eltávolíthatjuk az átlós mátrixot, így az új egyenlet:

legyen r az u felhasználó és az I elem besorolása, p az M sor egy felhasználó számára, Q pedig az(U) transzponálás oszlopa egy adott elemre i. tehát az egyenlet lesz:

megjegyzés — ha k sűrű mátrix értéke, mint m lesz sajátvektor a K*transzponálás(k), hasonlóan az u értéke lesz sajátvektor a transzponálás(k)*k, de a mátrixunk ritka mátrix, nem tudjuk kiszámítani u és m ezzel a megközelítéssel

tehát itt a feladatunk hogy megtaláljuk az M és U mátrixot . Az egyik módszer a véletlen érték inicializálása M – re és U-ra, és összehasonlítása az eredeti K Mátrixszal, ha az érték közel van K-hoz, majd leállítja az eljárást, különben minimalizálja az U és M értékét, amíg közel nem lesznek K-hoz . Az ilyen típusú optimalizálás folyamatát gradiens süllyedésnek nevezzük

tehát alapvető feladatunk az átlagos négyzethiba függvény minimalizálása, amely a következőképpen ábrázolható :

As our main task is to minimize the error i.e. meg kell találnunk, hogy melyik irányba kell mennünk, hogy meg kell különböztetnünk, ezért az új egyenlet lesz

div >

ezért a P és U frissített értéke most lesz:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Ezen döntési vonal alapján meg tudjuk különböztetni az adatok eloszlását

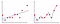
a 2. ábrán az első ábra az, ahol a modell lineárisan van felszerelve, míg a második ábrán polinom fokozattal van felszerelve. Első pillantásra úgy tűnik, hogy a második cselekmény sokkal jobb, mint az első, mivel 99% – os pontosságot ad a képzési adatokon, de mi van, ha bevezetjük a tesztadatokat, és 50% – os pontosságot ad a tesztadatokon . Ezt a fajta problémát nevezik overfitting és leküzdeni ezt a problémát vezetünk be egy fogalom az úgynevezett regularization.

mivel a túlillesztési probléma gyakori a gépi tanulásban, ezért kétféle szabályozási megközelítés létezik, amelyek felhasználhatók a túlillesztés eltávolítására

1-L1 szabályozás

2-L2 szabályozás

L1 szabályozás az együttható lineáris nagyságát adja büntetési kifejezésként, míg az L2-ben az együttható négyzet nagyságát adja a veszteségfüggvényhez/hiba függvényhez (amint azt fentebb tárgyaltuk). Az L1 ritka mátrixokat ad vissza, míg az L2 nem. Az L1 rendszeresítés jól működik a funkcióválasztásban ritka mátrixban.

az ajánlási adatkészletben is nagy az esély az adatok túlillesztésére. Tehát a túlillesztési probléma eltávolításához hozzáadhatjuk az L2 szabályozást (mivel a mátrix már ritka, itt nincs szükségünk L1 szabályozásra) a veszteségfüggvényben, ezért a veszteségfüggvény új egyenlete lesz:

ismét megtalálhatjuk a gradienst a frissített MSE-n, és frissített pontokat kaphatunk a fent tárgyalt megközelítés követésével

az egyik fontos dolog, amelyet figyelembe kell venni a fenti forgatókönyvben, a P és Q mátrix nem negatív, ezért az ilyen típusú faktorizációt nem negatív faktorizációnak is nevezik. Mivel a nem negatív faktorizáció automatikusan kivonja az információkat a nem negatív vektorkészletről. Az NMF-et széles körben használják a képfeldolgozásban, a szövegbányászatban, a nagy dimenziós adatok elemzésében