projekt Nayuki
definíció: a Fibonacci szekvencia meghatározása: \(F(0) = 0\), \(F (1) = 1\), és \(F(n) = F(n-1) + F(n-2)\) A \(N 6\). Tehát a szekvencia (kezdve \(F (0)\)) Az 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
ha egyetlen kifejezést akarunk kiszámítani a sorrendben(például \(F (n)\)), akkor erre néhány algoritmus van. Egyes algoritmusok sokkal gyorsabbak, mint mások.
algoritmusok
tankönyv rekurzív (rendkívül lassú)
naiv módon közvetlenül végrehajthatjuk az ismétlődést a Fibonacci-szekvencia matematikai definíciójában megadott módon. Sajnos, ez reménytelenül lassú: használ\ (\(N)\) verem tér és\ (~(^n)\) aritmetikai műveletek, ahol \ (~=\frac{\sqrt{5} + 1}{2}\) (aranyarány). Más szavakkal, a \(F(n)\) kiszámításához szükséges műveletek száma arányos a végső numerikus válaszral, amely exponenciálisan növekszik.
dinamikus programozás (lassú)
egyértelműnek kell lennie, hogy ha már kiszámoltuk \(F(k-2)\) és \(F(k-1)\), akkor hozzáadhatjuk őket, hogy \(F(k)\). Ezután adjuk hozzá \(F(k-1)\) és \(F(k)\), hogy \(F (k+1)\). Addig ismételjük, amíg el nem érjük \(k = n\). A legtöbb ember automatikusan észreveszi ezt az algoritmust, különösen a Fibonacci kézi számításakor. Ez az algoritmus a \(++(1)\) szóközt és a \(++(n)\) műveleteket veszi igénybe.
mátrix hatványozás (gyors)
az algoritmus ezen az ártatlan kinézetű azonosságon alapul (amely matematikai indukcióval bizonyítható):
\ (\left^n = \left \).
fontos, hogy az exponenciálást négyszögesítsük ezzel az algoritmussal, mert különben a dinamikus programozási algoritmussá degenerálódik. Ez az algoritmus a \(++(1)\) szóközt és \(\Log n)\) műveleteket veszi igénybe. (Megjegyzés: A bigint aritmetikai műveletek számát számoljuk, nem pedig a rögzített szélességű szóműveleteket.)
gyors duplázás(gyorsabb)
Adott \(F(k)\) és \(F (k+1)\), ezeket kiszámíthatjuk:
\(\begin{align}F(2K) &= F (k) \bal. \\F (2K + 1)&= F(k+1)^2 + F(k)^2.\end{align}\)
Ezek az identitások kivonhatók a mátrix hatványozási algoritmusából. Bizonyos értelemben ez az algoritmus a mátrix hatványozási algoritmus a redundáns számítások eltávolításával. Állandó tényezőnek kell lennie gyorsabb, mint a mátrix hatványozása, de az aszimptotikus idő komplexitása továbbra is ugyanaz.
összefoglalás: a két gyors Fibonacci algoritmus a mátrix exponenciálás és a gyors duplázás, amelyek mindegyikének \(\Log N)\) BigInt aritmetikai műveleteinek aszimptotikus komplexitása van. Mindkét algoritmus szorzást használ, így még gyorsabbá válnak, ha Karatsuba szorzást használnak. A másik két algoritmus lassú; csak összeadást használnak, szorzást nem.
forráskód
a megvalósítások több nyelven érhetők el:
-
Java: FastFibonacci.java (minden 3 algoritmusok, időzítés benchmark, futtatható fő program)
-
Python: fastfibonacci.py (csak gyors duplázás funkció)
-
Haskell: fastfibonacci.hs (csak gyors duplázási funkció)
-
C#: FastFibonacci.cs (csak gyors duplázás, futtatható főprogram)
(szükséges. NET Framework 4.0 vagy újabb; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
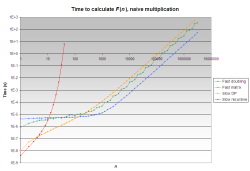
All algorithms, naive multiplication
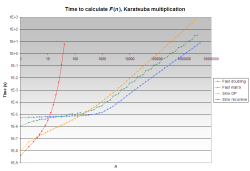
All algorithms, Karatsuba multiplication
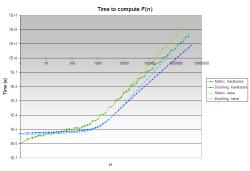
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive |
|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||
| 3 981 072 | 7 654 000 000 |
minden idő nanoszekundumban (ns) van megadva, 4 jelentős számnak adva. Az összes fenti tesztet az Intel Core 2 Quad Q6600-on (2,40 GHz) hajtottuk végre egyetlen szál segítségével, Windows XP SP 3, Java 1.6.0_22.
igazolások
mátrix hatványozás
gyenge indukcióval fogjuk igazolni ezt az azonosságot.
alapeset
\(n = 1\), egyértelműen \( \left^1 = \left \).
indukciós lépés
tegyük fel, hogy \(n 1\) \ (\left^n = \ left\). Ezután:
\(\bal^{n + 1} \ \ = \ Bal^N \ bal \ \ = \ bal \ bal \ \ = \ bal.\)
gyors duplázás
feltételezzük azt a tényt, hogy a mátrix hatványozási módszer helyes minden \(n 1\) esetében.
\(\bal \ \ = \ bal^{2n} \ \ = \ bal (\bal^n \ jobb)^2 \ \ = \ Bal^2 \ \ = \ bal.\)
ezért a mátrix celláinak egyenlőségével:
\(\begin{align}F (2n+1) &= F(n + 1)^2 + F(n)^2. \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)