Roche limit
az a korlátozó távolság, amelyre a műhold felszakadás nélkül megközelíthet, a műhold merevségétől függ. Az egyik végletben egy teljesen merev műhold megőrzi alakját, amíg az árapályerők szét nem törik. A másik végletben egy erősen folyékony műhold fokozatosan deformálódik, ami megnövekedett árapályerőkhöz vezet, ami a műhold megnyúlását okozza, tovább növelve az árapályerőket, és könnyebben szétesik.
a legtöbb valódi műhold valahol e két véglet között fekszik, szakítószilárdsága miatt a műhold sem tökéletesen merev, sem tökéletesen folyékony. Például egy törmelékhalom aszteroida inkább folyadékként viselkedik, mint szilárd köves; egy jeges test eleinte meglehetősen mereven viselkedik, de folyékonyabbá válik, amikor az árapály melegítése felhalmozódik, és jégei olvadni kezdenek.
de vegye figyelembe, hogy a fent meghatározottak szerint a Roche-határ olyan testre vonatkozik, amelyet kizárólag a gravitációs erők tartanak össze, amelyek egyébként nem kapcsolódó részecskéket egyesítenek, így alkotják a kérdéses testet. A Roche-határértéket általában egy Körpálya esetére is kiszámítják, bár egyszerű módosítani a számítást, hogy alkalmazható legyen az esetre (például) egy olyan test esetében, amely parabolikus vagy hiperbolikus pályán halad át az elsődlegesen.
merev-műholdas számításszerkesztés
a merev testű Roche-határ egy gömb alakú műhold egyszerűsített számítása. A szabálytalan alakzatokat, például a test árapály deformációját vagy az elsődleges pályáját elhanyagolják. Feltételezzük, hogy hidrosztatikus egyensúlyban van. Ezek a feltételezések, bár irreálisak, nagyban leegyszerűsítik a számításokat.
a merev Gömbös műhold Roche-határa a távolság , d {\displaystyle d}

, attól a primertől, amelynél a vizsgált tömegre gyakorolt gravitációs erő a tárgy felszínén pontosan megegyezik azzal az árapályerővel, amely a tömeget a tárgytól távol tartja: d = R M ( 2! \m!\m ) 1 3 {\displaystyle d=R_{M} \balra(2 {\frac {\rho _{M}} {\rho _{m}}}\jobbra)^{\frac {1}{3}}}

ahol R m {\displaystyle R_{M}}

az elsődleges sugara, 6 m {\displaystyle \rho _{M}}

az az elsődleges sűrűség, és ~ m {\displaystyle \Rho _{m}}

a műhold sűrűsége. Ez ekvivalens módon írható d = R m ( 2 M M M m ) 1 3 {\displaystyle d=R_{m}\balra(2{\frac {M_{M}}{m_{m}}}\jobbra)^{\frac {1}{3}}}

ahol R m {\displaystyle R_{m}}

a szekunder sugara, M m {\displaystyle M_{M}}

az elsődleges tömege, és m m {\displaystyle M_{M}}

a szekunder tömege.
Ez nem az objektumok méretétől, hanem a sűrűség arányától függ. Ez az a pályatávolság, amelyen belül az elsődlegeshez legközelebb eső műhold felszínén laza anyag (pl. regolith) elhúzódna, és hasonlóképpen az elsődlegessel szemközti oldalon lévő anyag is távolodik a műholdtól, nem pedig felé.
vegye figyelembe, hogy ez egy hozzávetőleges eredmény, mivel a tehetetlenségi erő és a merev szerkezet figyelmen kívül hagyja a levezetését.
az orbitális periódus ezután csak a szekunder sűrűségétől függ: a P = 2 π ( d 3 G M M ) 1 / 2 = 2 π ( d 3 ( 4 / 3 ) π G R a M 3 ρ M ) 1 / 2 = 6 π G ρ m {\displaystyle P=2\pi \left({\frac {d^{3}}{GM_{M}}}\right)^{1/2}=2\pi \left({\frac {d^{3}}{(4/3)\pi GR_{M}^{3}\rho _{M}}}\right)^{1/2}={\sqrt {\frac {6\pi }{G\rho _{m}}}}}

ahol G a gravitációs állandó. Például a sűrűség 3.346 g / cc (Holdunk sűrűsége) 2,552 órás orbitális periódusnak felel meg.
A képlet Levezetéseedit
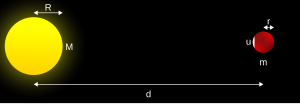
a Roche-határ meghatározásához Vegyünk egy kis tömeget u {\displaystyle u}

az elsődlegeshez legközelebb eső műhold felületén. Két erő van ezen a tömegen u {\displaystyle u}

: a gravitációs vonzás a műhold felé, a gravitációs vonzás az elsődleges felé. Tegyük fel, hogy a műhold szabadon esik az elsődleges körül, és hogy az árapályerő az egyetlen releváns kifejezés az elsődleges gravitációs vonzására. Ez a feltételezés egyszerűsítés, mivel a szabad esés csak a bolygó központjára vonatkozik, de elegendő lesz ehhez a levezetéshez.
a gravitációs húzás F G {\displaystyle F_{\text{G}}}

az u tömegen {\displaystyle u}

az m tömegű műhold felé displaystyle m}

és sugár r {\displaystyle R}

kifejezhető Newton gravitációs törvénye szerint. F G = G m u r 2 {\displaystyle F_{\text{G}}={\Frac {Gmu}{r^{2}}}

az árapály erő F T {\displaystyle F_{\text{T}}}

az u {\displaystyle u} tömegen

az R sugarú primer felé {\displaystyle R}

és m tömeg {\displaystyle m}

, d {\displaystyle d}

távolságban a két test középpontja között, körülbelül F T = 2 G M u r d 3 {\displaystyle F_ {\text{T}}={\frac {2gmur}{d^{3}}}}

.
ennek a közelítésnek a megszerzéséhez keresse meg az elsődleges gravitációs vonzásának különbségét a műhold közepén és az elsődlegeshez legközelebb eső műhold szélén:
F T = G M u ( d − r ) 2 − G M u d 2 {\displaystyle F_{\text{T}}={\frac {GMu}{(d-r)^{2}}}-{\frac {GMu}{d^{2}}}}

F T = G M u d 2 − ( d − r ) 2 d 2 ( d − r ) 2 {\displaystyle F_{\text{T}}=GMu{\frac {d^{2}-(d-r)^{2}}{d^{2}(d-r)^{2}}}}

F T = G M u 2 d r − r 2 d 4 − 2 d 3 r + r 2 d 2 {\displaystyle F_{\text{T}}=GMu{\frac {2dr-r^{2}}{d^{4}-2d^{3}r+r^{2}d^{2}}}}

abban a közelítésben , ahol r kb r {\displaystyle r\ll R}

és R < d {\displaystyle R<d}

, azt mondhatjuk, hogy az R 2 {\displaystyle R^{2}}

a számlálóban és minden r {\displaystyle R}

a nevezőben nulla lesz, ami: F T = G M u 2 d r d 4 {\displaystyle F_{\text{T}}=GMu{\frac {2dr}{d^{4}}}}

F T = 2 G M u r d 3 {\displaystyle F_{\text{T}}={\frac {2GMur}{d^{3}}}}

The Roche limit is reached when the gravitational force and the tidal force balance each other out.
F G = F T {\displaystyle F_{\text{G}}=F_{\text{T}}\;}

vagy
G m U r 2 = 2 G M U r d 3 {\displaystyle {\frac {Gmu}{r^{2}}}={\frac {2gmur}{d^{3}}}}
 {\displaystyle d}
{\displaystyle d}

, mint D = R ( 2 m m ) 1 3 {\displaystyle D=R\bal(2\, {\frac {m}{m}}\jobb)^{\frac {1}{3}}}

a műhold sugara nem jelenhet meg a határ kifejezésében, ezért a sűrűség szempontjából újraírják.
egy gömb esetében az M {\displaystyle M}

tömeg úgy írható, hogy M = 4 m r 3 3 {\displaystyle m = {\frac {4\pi \Rho _{M} R^{3}}{3}}}

ahol R {\displaystyle R}

az elsődleges sugara.
és hasonlóképp
m = 4 m r 3 3 {\displaystyle m = {\frac {4\pi \Rho _{m} r^{3}}{3}}}

ahol r {\displaystyle r}

a műhold sugara.
Helyettesítik a tömegek, az egyenlet a Roche korlátozza, illetve megszüntetik 4 π / 3 {\displaystyle 4\pi /3}

ad d = r ( 2 ρ M R 3 ρ m r 3 ) 1 / 3 {\displaystyle d=r\left({\frac {2\rho _{M}R^{3}}{\rho _{m}k^{3}}}\right)^{1/3}}

,

.
pontosabb képletszerkesztés
mivel egy közeli műhold valószínűleg közel kör alakú pályán kering szinkron forgással, fontolja meg, hogy a forgásból származó centrifugális erő hogyan befolyásolja az eredményeket. Ez az erő
F C = 2 U R = G M u r d 3 {\displaystyle F_{C} = \ omega ^{2}ur={\Frac {GMur}{d^{3}}}

és hozzáadódik a FT-hoz. Az erőegyensúly kiszámításával a következő eredményt kapjuk a Roche-határértékre vonatkozóan:
d = R M ( 3, m, m ) 1 3, 1,442 R M ( M, M, M ) 1 3, {\displaystyle d=R_{m}\balra(3, {\frac {\rho _{M}} {\rho _{m}}}\jobbra)^{\frac {1}, {3}}\kb 1.442r_{M}\balra ({\frac {\Rho _{m}} {\Rho _{m}}}\jobbra)^{\frac {1}{3}}}

………. (1)
vagy: d = R m ( 3 M M m ) 1 3 db 1,442 M M ( M M M ) 1 3 {\displaystyle d=R_{m}\balra(3\;{\frac {M_{M}}{m_{m}}}\jobbra)^{\frac {1}{3}}\kb 1.442r_{m}\balra({\frac {M_{M}}{m_{m}}}})^{\frac {1}{3}}}

………. (2)
használja az m = 4 m r 3 3 {\displaystyle m = {\frac {4\pi \Rho _{m} r^{3}}{3}}}

(ahol r {\displaystyle r}

a műhold sugara), hogy felváltsa az! m {\displaystyle \rho _{m}}

az(1) képletben lehet egy harmadik képletünk is:
D = ( 9 m m 4 fő ) 1 3 0,8947 fő ( m fő ) 1 3 {\displaystyle D=\Bal({\FRAC {9m_{m}}{4\pi \Rho _{m}}}\jobb)^{\frac {1}{3}}\kb 0.8947 \ left ({\frac {M_{M}} {\rho _ {m}}} \ right)^{\frac {1}{3}}}

………. (3)
tehát elegendő megfigyelni a csillag (bolygó) tömegét és megbecsülni a bolygó (műhold) sűrűségét, hogy kiszámítsuk a bolygó (műhold) Roche-határát a csillag (bolygó) rendszerben.
Roche-határ, domb-gömb és a bolygó sugara
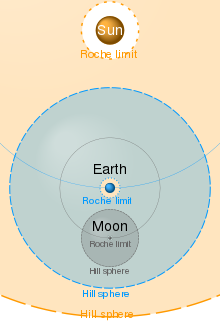
tekintsünk meg egy bolygót, amelynek sűrűsége kb m {\displaystyle \Rho _{m}}

sugara R {\displaystyle R}

a csillag withis a fizikai jelentése Roche határ, Roche lebeny és Hill sphere. a
képlet(2) a következőképpen írható le: R Roche = R domb 3 M m 3 = r másodlagos 3 M m 3 {\displaystyle R_{\text{Roche}}=R_{\text{Hill}}{\sqrt{\frac {3M}{m}}}=R_{\text{secondary}}{\sqrt{\frac {3M}{m}}}}

, tökéletes matematikai szimmetria.
Ez a Roche limit és a Hill sphere csillagászati jelentősége.
Megjegyzés: A Roche limit és a Hill sphere teljesen különböznek egymástól, de mindkettő az O. D. Douard Roche munkája.
a csillagászati test Dombgömbje az a régió, amelyben uralja a műholdak vonzerejét, míg a Roche-határ az a minimális távolság, amelyig a műhold megközelítheti elsődleges testét anélkül, hogy árapályerő legyőzné a műholdat összetartó belső gravitációt.
a csillagászati test Dombgömbje az a régió, amelyben uralja a műholdak vonzerejét, míg a Roche-határ az a minimális távolság, amelyig a műhold megközelítheti elsődleges testét anélkül, hogy árapályerő legyőzné a műholdat összetartó belső gravitációt.
Fluid satellitesEdit
a Roche-határ kiszámításának pontosabb megközelítése figyelembe veszi a műhold deformációját. Szélsőséges példa lehet egy árapályosan lezárt folyékony műhold, amely egy bolygó körül kering, ahol a műholdra ható bármilyen erő prolát gömbössé deformálná.
a számítás összetett, eredménye nem ábrázolható pontos algebrai képletben. Maga Roche a következő közelítő megoldást vezette le a Roche-határértékre:
d 2.44 r (6.44 r) 1 / 3 {\displaystyle d \ KB 2.44 r \ bal ({\frac {\rho _ {M}} {\rho _ {m}}} \ jobb)^{1/3}}

azonban egy jobb közelítés, amely figyelembe veszi az elsődleges oblatenitását és a műhold tömegét, a következő:
d 6,423 R ( M ) 1 / 3 ( ( 1 + m 3 M ) + c 3 R ( 1 + m M ) 1 − c / R ) 1 / 3 {\displaystyle d\approx 2.423 r\bal({\frac {\Rho _{m}}{\Rho _{m}}}\jobb)^{1/3}\bal({\frac {(1+{\frac {m}{3m}})+{\frac {c}{3R}}(1+{\frac {m}{m}})}{1-c/R}}\jobb)^{1/3}}

ahol c / R {\displaystyle c/R}

az elsődleges oblatenitása. A numerikus tényezőt számítógép segítségével számítják ki.
a folyékony oldat alkalmas olyan testekre, amelyek csak lazán vannak együtt tartva, például egy üstökös. Például üstökös Shoemaker–Levy 9a Jupiter körüli bomló pályája 1992 júliusában túllépte Roche határát,aminek következtében számos kisebb darabra töredezett. A következő megközelítéskor 1994-ben a töredékek a bolygóra zuhantak. A Shoemaker–Levy 9-et először 1993-ban figyelték meg, de pályája azt jelezte, hogy a Jupiter néhány évtizeddel korábban elfogta.
A képletszerkesztés
mivel a folyékony műholdas eset finomabb, mint a merev, a műholdat néhány egyszerűsítő feltevéssel írják le. Először tegyük fel, hogy az objektum összenyomhatatlan folyadékból áll, amelynek sűrűsége állandó, melynek sűrűsége nem függ sem külső, sem belső erőktől. \m {\displaystyle\rho _{m}}

és v {\displaystyle v}

térfogatú.
másodszor, tegyük fel, hogy a műhold körkörös pályán mozog, és szinkron forgásban marad. Ez azt jelenti, hogy az a szögsebesség, amellyel a tömegközéppontja körül forog, megegyezik azzal a szögsebességgel, amellyel a rendszer teljes baricentruma körül mozog.
a szögsebességet a Kepler harmadik törvénye adja meg: 6=g M + m d 3. displaystyle \omega}

. {\displaystyle \ omega ^{2} = G\, {\frac {M + m}{d^{3}}}.}

Ha M sokkal nagyobb, mint m, Ez közel lesz
2 = g m d 3 . {\displaystyle \ omega ^{2} = G\, {\frac {M}{d^{3}}}.}

a szinkron forgatás azt jelenti, hogy a folyadék nem mozog, és a probléma statikusnak tekinthető. Ezért a folyadék viszkozitása és súrlódása ebben a modellben nem játszik szerepet, mivel ezek a mennyiségek csak a mozgó folyadék számára játszanak szerepet.
ezeket a feltételezéseket figyelembe véve a következő erőket kell figyelembe venni:
- a gravitációs erő miatt a fő test;
- a centrifugális erő a forgó referenciarendszer; és
- az öngravitációs mező a műhold.
mivel ezek az erők konzervatívak, kifejezhetők egy potenciál segítségével. Sőt,a műhold felülete ekvipotenciális. Ellenkező esetben a potenciálkülönbségek a folyadék egyes részeinek a felszínen történő mozgását és mozgását eredményeznék, ami ellentmond a statikus modell feltételezésének. Tekintettel a fő testtől való távolságra, meg kell határozni a felület azon formáját, amely megfelel az ekvipotenciális állapotnak.

mivel a pályát körkörösnek feltételezték, a fő testre ható teljes gravitációs erő és az orbitális centrifugális erő megszűnik. Két erő marad: az árapályerő és a forgó centrifugális erő. Az árapályerő a tömegközépponthoz viszonyított helyzettől függ, amelyet a merev modellben már figyelembe vettek. Kis testek esetében a folyékony részecskék távolsága a test közepétől kicsi a D távolsághoz képest a fő testhez képest. Így az árapályerő linearizálható,ami ugyanazt a képletet eredményezi az FT-re, mint a fentiekben.
míg ez az erő a merev modellben csak a műhold r sugarától függ, a folyadék esetében a felület összes pontját figyelembe kell venni, az árapályerő pedig a Tömegközépponttól a műholdat és a fő testet összekötő vonalon kivetített adott részecskéig terjedő távolságtól függ. A radiális távolságnak hívjuk az addictive distance-t. Mivel az árapály erő lineáris Δd, a kapcsolódó potenciális arányos a tér a változó, illetve a m ≪ M {\displaystyle m\ll M}

mi a V a T = − 3 G M 2 d 3 Δ d 2 {\displaystyle V_{T}=-{\frac {3GM}{2d^{3}}}\Delta d^{2}\,}

Hasonlóképpen, a centrifugális erő egy esetleges
V C = − 1 2 ω 2 Δ d 2 = − G M-2 d 3 Δ d 2 {\displaystyle V_{C}=-{\frac {1}{2}}\omega ^{2}\Delta d^{2}=-{\frac {GM}{2d^{3}}}\Delta d^{2}\,}

forgási szögsebesség esetén a \\displaystyle\omega }

.
meg akarjuk határozni a műhold alakját, amelynél az öngravitációs potenciál és a VT + VC összege állandó a test felszínén. Általánosságban elmondható, hogy egy ilyen problémát nagyon nehéz megoldani, de ebben a konkrét esetben ügyes találgatással megoldható, mivel az Árapálypotenciál Négyzetfüggése a sugárirányú távolságtól az első közelítésig, figyelmen kívül hagyhatjuk a centrifugális potenciált VC és csak az árapálypotenciált vesszük figyelembe VT.
mivel a potenciális VT csak egy irányban változik, azaz a fő test felé, a műhold várhatóan axiálisan szimmetrikus formát ölt. Pontosabban, feltételezhetjük, hogy a forradalom szilárd formáját ölti. Az ilyen forradalmi szilárd anyag felületén lévő önpotenciál csak a tömegközéppont sugárirányú távolságától függhet. Valójában a műhold metszéspontja és a testeket összekötő vonalra merőleges sík egy olyan lemez, amelynek határa feltételezéseink szerint állandó potenciálú kör. Ha az öngravitációs potenciál és a VT közötti különbség állandó, akkor mindkét potenciálnak ugyanúgy kell függenie a Xhamd-től. Más szavakkal, az önpotenciálnak arányosnak kell lennie a négyzetével. Ezután megmutatható, hogy az ekvipotenciális megoldás a forradalom ellipszoidja. Állandó sűrűség és térfogat esetén az ilyen test önpotenciálja csak az ellipszoid excentricitásától függ:
V s = V s 0 + g , {\displaystyle V_{s}=v_{s_{0}}+g\pi \Rho _{m}\cdot F (\varepsilon) \cdot \Delta D^{2},}

ahol V S 0 {\displaystyle v_{s_{0}}}

az állandó Önpotenciál a test kör alakú élének és a központi szimmetriasík, amelyet az egyenlet ad meg 6d=0.
az F dimenzión kívüli függvényt az ellipszoid potenciáljának pontos megoldásából kell meghatározni
f ( 6 ) = 1 − 2, 3, {\displaystyle f(\varepsilon )={\frac {1-\varepsilon ^{2}}{\varepsilon ^{3}}}\cdot \left}

és meglepő módon nem függ a műhold hangerejétől.

bár az f függvény explicit formája bonyolultnak tűnik, egyértelmű, hogy kiválaszthatjuk és meg is választhatjuk az értékét úgy, hogy a potenciális VT egyenlő legyen VS plusz egy állandó, amely független a változótól. Ellenőrzéssel ez akkor fordul elő, amikor
2 g

Ez az egyenlet numerikusan megoldható. A grafikon azt jelzi, hogy két megoldás létezik, így a kisebb a stabil egyensúlyi formát (a kisebb excentricitású ellipszoidot) képviseli. Ez a megoldás meghatározza az árapály ellipszoid excentricitását a fő testtől való távolság függvényében. Az f függvény deriváltjának nulla van, ahol a maximális excentricitást elérjük. Ez megfelel a Roche-határértéknek.
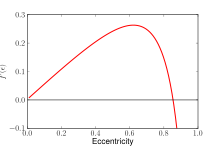
pontosabban a Roche-határértéket az a tény határozza meg, hogy az f függvény, amely az ellipszoidot gömb alak felé szorító erő nemlineáris mértékének tekinthető, úgy van korlátozva, hogy van egy excentricitás, amelynél ez az összehúzó erő maximálissá válik. Mivel az árapályerő növekszik, amikor a műhold megközelíti a fő testet, egyértelmű, hogy van egy kritikus távolság, amelyen az ellipszoid felszakad.
a maximális excentricitás számszerűen kiszámítható az F’deriváltjának nullájaként. Az egyik a
– t kapja, Max. 0-t . 86 {\displaystyle \ varepsilon _{\text{max}} \ approx 0{.}86}

ami megfelel az ellipszoid tengelyek arányának 1: 1,95. Ezt beillesztve a függvény képletébe f meg lehet határozni azt a minimális távolságot, amelyen az ellipszoid létezik. Ez a Roche-határérték,
D 6 . 423 .O., R., M., M., M. 3. {\displaystyle d \ approx 2{.}423 \ cdot R \ cdot {\sqrt {\frac {\rho _ {M}} {\rho _ {m}}}}\,.}

meglepő módon a centrifugális potenciállal együtt rendkívül kevés különbség van, bár az objektum a Roche ellipszoid, egy általános háromtengelyes ellipszoid, amelynek minden tengelye különböző hosszúságú. A potenciál a tengelyhossz sokkal bonyolultabb függvényévé válik, elliptikus funkciókat igényel. A megoldás azonban sokkal tovább halad, mint a csak árapályos esetben, és
D 2-t találunk . 455 .O., R., M., M., M. 3. {\displaystyle d \ approx 2{.}455 \ cdot R \ cdot {\sqrt {\frac {\rho _ {M}} {\rho _ {m}}}}\,.}
