デジタル世界の時代には、我々はそれが電子商取引のウェブサイトやエンターテイメントのウェブサイトやソーシャ 推奨は、ユーザーに（過去の活動に基づいて）推奨される選択を与えるだけでなく、ユーザーの行動（感傷的分析または感情AI）についても伝えます。

まず、勧告が何であるかを理解しましょう。 基本的には、過去の検索/活動に基づいてユーザーにアイテムを推薦しています。

図1は、過去の閲覧履歴と過去の検索に基づいてAmazonの推奨事項を示しています。 したがって、勧告は基本的に過去の行動に基づいて将来の行動を予測することであると言うことができます。 推奨システムで使用されているアプローチの二つのタイプがあります

1-コンテンツベースのフィルタリング

2-共同ベースのフィルタリング

コンテンツベースのフィルタリング-

これは、Kによって高く評価された前の項目に似ているユーザー Kに項目を推薦するという考えに基づいています。 コンテンツベースのフィルタリングは、推奨事項の透明性を示していますが、コラボレーションフィルタリングとは異なり、大きなデータに対して効率的に作業することはできません

コラボレーションベースのフィルタリング

これは、特定の種類のアイテムに同じ関心を共有する人々は、基本的にメタデータに依存しているコンテンツベースとは異なり、実生活の活動を扱っている他の種類のアイテムにも同じ関心を共有するという考えに基づいています。 このタイプのフィルタリングは、ほとんどのドメインに柔軟性があります（またはドメインフリーと言うことができます）が、コールドスタートの問題のため、データのスパース性（マトリックス因数分解によって処理されました）これらのタイプのアルゴリズムは、いくつかのシナリオでいくつかの後退に直面しています。

マトリックス因数分解

マトリックス因数分解は、Netflixの競争（2006）の後に脚光を浴びていますNetflixは、そのルート平均二乗性能を10％向上させる人にprize1百万の賞金を発表しました。 Netflixは、480,189人のユーザーが17,770本の映画に与えた100,480,507の評価のトレーニングデータセットを提供しました。

行列分解は、行列m*nがm*kとk*nに分解される協調ベースのフィルタリング方法です。 基本的には複素行列演算の計算に使用されます。 行列の除算は、因数分解された行列を乗算すると、図2に示すように元の行列が得られるようなものです。 これは、二つのエンティティ間の潜在的な特徴を発見するために使用されます（二つ以上のエンティティに使用することができますが、これはテンソル図2: 行列分解-ソース

行列分解は三つのタイプに分類することができます-

1-LU分解—lは下三角行列であり、Uは上三角行列であり、一般的に線形回帰の係数を見つけるために使用されるLとU行列への行列の分解。 行列が簡単に分解できない場合、この分解は失敗しました

2-QR行列分解-行列をQとRに分解します。Qは正方行列であり、Rは上三角行列（必要な正方 固有システム解析に使用されます

3-コレスキー分解-これは機械学習で主に使用される分解です。 線形回帰のための線形最小二乗を計算するために使用されます

行列分解は、画像認識、推奨などの様々なドメインで使用することができます。 このタイプの問題で使用される行列は、あるユーザーがいくつかの映画のみを評価する可能性があるため、一般的にまばらです。 行列因数分解には、次元削減（次元削減の詳細については次元の呪いを参照してください）、潜在値分解

問題文

表1では、各ユーザーが映画を評価できる5人のユーザーと6人の映画があります。 私たちはヘンリーがトールのために評価しなかったことを見ることができるように、ロッキーは同様にジェリーがアバターのために評価しませんでした。 実世界のシナリオでは、これらのタイプの行列は非常に疎な行列になる可能性があります

私たちの問題文は、表1に示すように未評価の映画の評価を見つけなければならないことです

行列分解によってユーザーの評価を見つけることを目的としていますが、その前に特異値分解（svd）を通過する必要 SVDの深さに行く前に、最初にKとtranspose（K）が何であるかを理解することができます。 行列K（表1）でPCAを実行すると、すべてのユーザーベクトルが取得されます。 その後、これらのベクトルを行列Uの列に入れることができ、transpose(K)でPCAを実行すると、行列Mの列になるすべてのムービーベクトルが得られます。

Kとtranspose(K)でPCAを別々に実行する代わりに、Kとtranspose(K)でPCAをシングルショットで実行できるSVDを使用することができます。 SVDは基本的に行列Kを行列U、行列M、対角行列に因数分解します:Div>

Kは元の行列で、Uはユーザーです簡単にするために、我々はしばらくの間対角行列を削除することができますので、新しい方程式は次のようになります:/div>

Let rはユーザー uとアイテムiに対して定義された評価です、pはユーザーのmの行であり、qは特定の項目iのtranspose（u）の列です。:

注—kがmよりも密な行列値であれば、k*transpose(k)の固有ベクトルになりますが、同様にuの値はtranspose(k)*kの固有ベクトルになりますが、行列は疎行列であり、このアプローチではuとmを計算することはできません

ここでのタスクは行列mとuを見つけることです。 1つの方法は、ランダムな値をMとUに初期化し、値がKに近い場合は元の行列Kと比較して、手続きを停止するか、そうでない場合はUとMの値をK これらのタイプの最適化のプロセスは、勾配降下と呼ばれます

したがって、私たちの基本的なタスクは、次のように表すことができる平均二乗誤差関数を最小化することです :

As our main task is to minimize the error i.e. 私たちはそれを区別しなければならないので、新しい方程式は

したがって、pとuの更新された値は次のようになります:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . その決定ラインに基づいて、データの分布を区別することができます

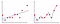
図2の最初のプロットでは、モデルが線形に近似され、第二のプロットでは多項式次数が近似されます。 最初の一見では、第二のプロットは、トレーニングデータに99％の精度を与えているので、最初のプロットよりもはるかに優れているように見えますが、テス このタイプの問題はoverfittingと呼ばれ、この問題を克服するために正則化と呼ばれる概念を導入します。

オーバーフィット問題は機械学習で一般的であるため、オーバーフィットを削除するために使用できる正則化アプローチの二つのタイプがあります

1-L1正則化

2-L2正則化

L1正則化はペナルティ項として係数の線形大きさを追加し、L2では損失関数/誤差関数に係数の二乗大きさを追加します（上記のように）。 L1はスパース行列を返しますが、L2はスパース行列を返しません。 L1正則化は、スパース行列の特徴選択でうまく機能します。

推奨データセットでも、データの過剰適合の可能性が高いです。 したがって、過剰適合問題を取り除くために、損失関数にL2正則化を追加することができます（行列はすでに疎であるため、ここではL1正則化は必:Div>

再び、更新されたMSE上の勾配を見つけることができ、更新されます上で議論したのと同じアプローチに従うことによるポイント

上記のシナリオで考慮すべき重要なことの一つは、行列pとqは非負であるため、これらのタイプの因数分解は非負因数分解とも呼ばれます。 非負の因数分解として、ベクトルの非負のセットの情報を自動的に抽出します。 NMFは、画像処理、テキストマイニング、高次元データの分析に広く使用されています