Project Nayuki
定義:フィボナッチ数列は\(F)として定義されます(0) = 0\), \(≥F(n)=F(n-1)+F(n-2)forとすると、≥f(n)=F(n-1)+F(n-2)=F(n-1)+F(n-2)=F(n-1)+F(n-2)=f(n-1)≥となります。 したがって、シーケンス(\(F(0)\)で始まる)は次のようになります0, 1, 1, 2, 3, 5, 8, 13, 21, ….シーケンス内の単一の項(例えば\(F(n)\))を計算したい場合は、そうするアルゴリズムがいくつかあります。 いくつかのアルゴリズムは、他のものよりもはるかに高速です。
アルゴリズム
教科書再帰的(非常に遅い)
単純に、フィボナッチ数列の数学的定義に与えられたように、再帰を直接実行することができま 残念ながら、それは絶望的に遅いです:それは\(Π(n)\)スタックスペースと\(Π(φ^n)\)算術演算を使用します。{5} + 1}{2}\) (黄金比)。 言い換えれば、\(F(n)\)を計算する演算の数は、指数関数的に増加する最終的な数値答えに比例します。すでに\(F(k-2)\)と\(F(k-1)\)を計算している場合、それらを追加して\(F(k)\)を得ることができることは明らかです。 次に、\(F(k-1)\)と\(F(k)\)を追加して\(F(k+1)\)を取得します。 私たちは\(k=n\)に達するまで繰り返します。 ほとんどの人は、特にフィボナッチを手作業で計算するときに、このアルゴリズムに自動的に気付きます。 このアルゴリズムは\(Σ(1)\)空間と\(Σ(n)\)演算を取ります。このアルゴリズムは、この無邪気に見える恒等式(数学的帰納法によって証明できる)に基づいています:
\(\left^n=\left\)。
このアルゴリズムで二乗することによって累乗を使用することが重要です。 このアルゴリズムは、\(Θ(1)\)スペースと\(Θ(\log n)\)操作を取ります。 (注: 固定幅の単語操作ではなく、bigint算術演算の数を数えています。F(k)\)と\(F(k+1)\)を考えると、これらを計算することができます。
\(\begin{align}F(2k)&=F(k)\left。 \=F(k+1)^2+F(k)^2です。これらの恒等式は、行列のべき乗アルゴリズムから抽出することができます。 ある意味では、このアルゴリズムは、冗長な計算を削除した行列べき乗アルゴリズムです。 それは行列のべき乗よりも速い一定の因子でなければなりませんが、漸近的な時間の複雑さは依然として同じです。要約:2つの高速フィボナッチアルゴリズムは、行列のべき乗と高速倍増であり、それぞれが\(log(\log n)\)bigint算術演算の漸近的複雑さを持ちます。 どちらのアルゴリズムも乗算を使用するため、カラツバ乗算を使用するとさらに高速になります。 他の2つのアルゴリズムは遅く、加算のみを使用し、乗算は使用しません。
ソースコード
実装は複数の言語で利用可能です。
-
Java: ファストフィボナッチjava(すべての3つのアルゴリズム、タイミングベンチマーク、実行可能なメインプログラム)
-
Python:fastfibonacci.py (高速倍増機能のみ)
-
Haskell:fastfibonacci。hs(高速倍増機能のみ)
-
C#:FastFibonacci。cs(高速倍増のみ、実行可能なメインプログラム)
(.NET Framework4.0以上が必要です; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
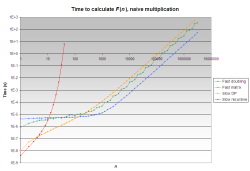
All algorithms, naive multiplication
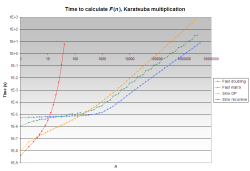
All algorithms, Karatsuba multiplication
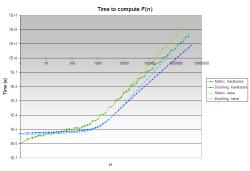
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 | ||||
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 | ||||
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 | ||||
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 | ||||
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 | ||||
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 | ||||
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 | ||||
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 | ||||
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 | ||||
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 | ||||
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 | ||||
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 | ||||
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 | ||||
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 | ||||
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |||||
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |||||
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |||||
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |||||
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |||||
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |||||
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |||||
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |||||
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |||||
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |||||
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |||||
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |||||
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |||||
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |||||
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |||||
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |||||
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |||||
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |||||
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |||||
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |||||
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |||||
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |||||
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |||||
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |||||
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |||||
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |||||
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |||||
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |||||
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |||||
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |||||
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |||||
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |||||
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |||||
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |||||
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |||||
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |||||
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |||||
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |||||
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |||||
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |||||
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |||||
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |||||
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |||||
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |||||
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |||||
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |||||
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |||||
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |||||
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||||||
| 3 981 072 | 7 654 000 000 |
すべての時間はナノ秒(ns)、4つの有効数字に与えられます。 上記のすべてのテストは、単一のスレッド、Windows XP SP3、Java1.6.0_22を使用して、Intel Core2Quad Q6600(2.40GHz)で実行されました。
証明
行列べき乗
この恒等式を証明するために弱い帰納法を使用します。
基本ケース
\(n=1\)、明らかに\(\left^1=\left\)です。帰納ステップ
は\(n≥1\)を\(\left^n=\left\)と仮定します。 とします。
\(\left^{n+1}\\=\left^n\左\\=\left\left\\=\left\\=\ります。私たちは、行列のべき乗法がすべての\(n≥1\)に対して正しいという事実を仮定します。\\左\=\左^{2n}\=\左(\左^n\右)2 2\=\左^2\=\左。したがって、行列内のセルを等式化することによって:
\(\begin{align}F(2n+1)&=F(n+1)2 2+F(n)^2。 \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)