projekt Nayuki
definicja: ciąg Fibonacciego jest zdefiniowany jako \(F(0) = 0\), \(F(1) = 1\) i \(f(n) = F(n-1) + F(n-2)\) dla \(N ≥ 2\). Więc ciąg (zaczynający się od \(F (0)\)) jest 0, 1, 1, 2, 3, 5, 8, 13, 21, ….
Jeśli chcemy obliczyć pojedynczy wyraz w sekwencji (np. \(f(n)\)), istnieje kilka algorytmów, aby to zrobić. Niektóre algorytmy są znacznie szybsze niż inne.
algorytmy
Podręcznik rekurencyjny (bardzo wolny)
naiwnie, możemy bezpośrednio wykonać powtarzalność jak podano w matematycznej definicji ciągu Fibonacciego. Niestety, jest beznadziejnie powolny: używa\ (Θ(n)\) przestrzeni stosu i\ (Θ (φ^n)\) operacji arytmetycznych, gdzie \(φ = \frac {\sqrt{5} + 1}{2}\) (złoty stosunek). Innymi słowy, liczba operacji do obliczenia \(F (n)\) jest proporcjonalna do ostatecznej odpowiedzi liczbowej, która rośnie wykładniczo.
programowanie dynamiczne (wolne)
powinno być jasne, że jeśli już obliczyliśmy \(F(k-2)\) i \(F(k-1)\), to możemy je dodać, aby uzyskać \(F(k)\). Następnie dodajemy \(F (k-1)\) i \(f (k)\), aby uzyskać \(F (k+1)\). Powtarzamy, aż osiągniemy \(k = N\). Większość ludzi zauważa ten algorytm automatycznie, zwłaszcza przy ręcznym obliczaniu Fibonacciego. Algorytm ten wykonuje operacje \(Θ(1)\) i\ (Θ (n)\).
wykładnik macierzy (szybki)
algorytm opiera się na tej niewinnie wyglądającej tożsamości (co można udowodnić za pomocą indukcji matematycznej):
\( \left^n = \left \).
ważne jest, aby użyć wykładnika przez kwadrat z tym algorytmem, ponieważ w przeciwnym razie degeneruje się do algorytmu programowania dynamicznego. Algorytm ten wykonuje operacje \(Θ(1)\) i \(Θ(\log N)\). (Uwaga: Liczymy liczbę operacji arytmetycznych biginta, a nie operacji słownych o stałej szerokości.
szybkie podwajanie (szybsze)
biorąc pod uwagę \(F(k)\) I \(F (k + 1)\), Możemy obliczyć te:
\(\begin{align}F(2K) & = F(k) \left. \\F(2K+1) & = F(k+1)^2 + F(k)^2.\end{align}\)
tożsamości te można wyodrębnić z algorytmu wykładnictwa macierzy. W pewnym sensie algorytm ten jest algorytmem wykładniczym macierzy z usuniętymi nadmiarowymi obliczeniami. Powinien być stałym czynnikiem szybszym niż wykładnik macierzy, ale asymptotyczna złożoność czasowa jest wciąż taka sama.
podsumowanie: dwa szybkie algorytmy Fibonacciego to wykładnik macierzy i szybkie podwajanie, z których każdy ma asymptotyczną złożoność \(Θ(\log N)\) operacji arytmetycznych biginta. Oba algorytmy używają mnożenia, dzięki czemu stają się jeszcze szybsze, gdy używa się mnożenia Karatsuba. Pozostałe dwa algorytmy są powolne; używają tylko dodawania i nie mnożenia.
kod źródłowy
implementacje są dostępne w wielu językach:
-
Java: FastFibonacci.java (wszystkie 3 algorytmy, benchmark czasowy, uruchamialny program główny)
-
Python: fastfibonacci.py (tylko Funkcja szybkiego podwajania)
-
Haskell: fastfibonacci.hs (tylko Funkcja szybkiego podwajania)
-
C#: FastFibonacci.cs(tylko szybkie podwajanie, uruchamialny program główny)
(wymaga. NET Framework 4.0 lub nowszego; compile withcsc /r:System.Numerics.dll fastfibonacci.cs)
Benchmarks
Graphs
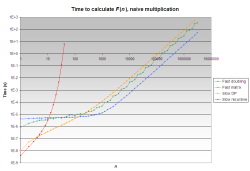
All algorithms, naive multiplication
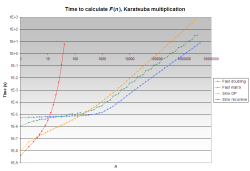
All algorithms, Karatsuba multiplication
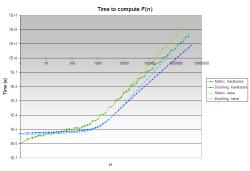
Fast algorithms, both multiplication algorithms
(Note: The graphs have logarithmic scales on the x and y axes.)
Table
| n | Fast doubling, Karatsuba multiplication | Fast matrix, Karatsuba multiplication | Fast doubling, naive multiplication | Fast matrix, naive multiplication | Slow dynamic programming | Slow recursive |
|---|---|---|---|---|---|---|
| 1 | 5 414 | 1 042 | 4 197 | 887 | 10 | 4 |
| 2 | 5 638 | 2 092 | 4 442 | 1 822 | 53 | 22 |
| 3 | 5 708 | 2 740 | 4 509 | 2 342 | 92 | 56 |
| 4 | 5 945 | 3 027 | 4 733 | 2 660 | 133 | 114 |
| 5 | 5 989 | 3 677 | 4 787 | 3 147 | 172 | 219 |
| 6 | 5 972 | 3 956 | 4 765 | 3 371 | 211 | 400 |
| 8 | 6 191 | 3 972 | 4 969 | 3 428 | 289 | 1 161 |
| 10 | 6 283 | 4 952 | 5 022 | 4 154 | 370 | 3 113 |
| 13 | 6 307 | 5 610 | 5 046 | 4 667 | 488 | 13 480 |
| 16 | 6 479 | 4 955 | 5 177 | 4 210 | 605 | 57 300 |
| 20 | 6 542 | 5 923 | 5 234 | 4 985 | 763 | 394 000 |
| 25 | 6 632 | 6 565 | 5 263 | 5 479 | 964 | 4 373 000 |
| 32 | 6 794 | 5 887 | 5 388 | 4 908 | 1 235 | 127 500 000 |
| 40 | 6 818 | 6 880 | 5 433 | 5 715 | 1 552 | 5 980 000 000 |
| 50 | 6 806 | 7 742 | 5 486 | 6 446 | 2 023 | |
| 63 | 6 931 | 10 180 | 5 589 | 8 339 | 2 598 | |
| 79 | 7 162 | 11 090 | 5 753 | 9 187 | 3 396 | |
| 100 | 7 279 | 9 225 | 5 904 | 7 717 | 4 472 | |
| 126 | 7 427 | 12 410 | 6 059 | 10 220 | 5 866 | |
| 158 | 7 600 | 13 090 | 6 141 | 10 900 | 7 888 | |
| 200 | 8 006 | 11 700 | 6 556 | 9 969 | 10 640 | |
| 251 | 8 146 | 15 660 | 6 672 | 13 060 | 14 280 | |
| 316 | 8 597 | 18 810 | 7 089 | 16 530 | 19 610 | |
| 398 | 9 501 | 20 550 | 8 078 | 18 120 | 27 650 | |
| 501 | 9 964 | 24 050 | 8 492 | 21 340 | 38 970 | |
| 631 | 11 070 | 38 790 | 9 510 | 35 720 | 55 540 | |
| 794 | 13 020 | 41 810 | 11 520 | 39 380 | 80 280 | |
| 1 000 | 14 660 | 50 870 | 13 130 | 48 230 | 118 000 | |
| 1 259 | 18 640 | 99 020 | 16 990 | 95 640 | 175 300 | |
| 1 585 | 25 300 | 113 500 | 23 660 | 110 800 | 263 000 | |
| 1 995 | 32 360 | 148 100 | 30 770 | 144 700 | 397 500 | |
| 2 512 | 45 540 | 314 800 | 43 980 | 311 400 | 608 800 | |
| 3 162 | 67 800 | 372 200 | 66 250 | 369 000 | 937 200 | |
| 3 981 | 98 560 | 491 500 | 96 780 | 488 100 | 1 457 000 | |
| 5 012 | 143 500 | 1 050 000 | 145 900 | 1 132 000 | 2 269 000 | |
| 6 310 | 214 100 | 1 284 000 | 227 700 | 1 357 000 | 3 546 000 | |
| 7 943 | 320 300 | 1 662 000 | 351 300 | 1 821 000 | 5 547 000 | |
| 10 000 | 466 400 | 3 519 000 | 538 400 | 4 382 000 | 8 700 000 | |
| 12 589 | 691 100 | 4 303 000 | 851 700 | 5 254 000 | 13 640 000 | |
| 15 849 | 1 007 000 | 5 481 000 | 1 310 000 | 7 079 000 | 21 440 000 | |
| 19 953 | 1 493 000 | 11 800 000 | 2 081 000 | 17 260 000 | 33 620 000 | |
| 25 119 | 2 185 000 | 13 620 000 | 3 296 000 | 20 710 000 | 53 030 000 | |
| 31 623 | 3 205 000 | 17 570 000 | 5 159 000 | 27 860 000 | 83 310 000 | |
| 39 811 | 4 637 000 | 36 800 000 | 8 109 000 | 68 540 000 | 131 500 000 | |
| 50 119 | 6 750 000 | 42 430 000 | 12 910 000 | 82 230 000 | 207 700 000 | |
| 63 096 | 9 913 000 | 54 770 000 | 20 410 000 | 110 600 000 | 326 900 000 | |
| 79 433 | 14 450 000 | 113 300 000 | 32 300 000 | 275 100 000 | 517 100 000 | |
| 100 000 | 20 800 000 | 130 600 000 | 51 640 000 | 330 700 000 | 819 700 000 | |
| 125 893 | 30 380 000 | 168 900 000 | 81 150 000 | 445 200 000 | 1 296 000 000 | |
| 158 489 | 44 090 000 | 346 800 000 | 129 200 000 | 1 103 000 000 | 2 058 000 000 | |
| 199 526 | 63 260 000 | 405 400 000 | 205 100 000 | 1 325 000 000 | 3 249 000 000 | |
| 251 189 | 92 330 000 | 517 300 000 | 325 100 000 | 1 766 000 000 | 5 153 000 000 | |
| 316 228 | 133 700 000 | 1 055 000 000 | 515 700 000 | 4 413 000 000 | 8 161 000 000 | |
| 398 107 | 191 900 000 | 1 228 000 000 | 815 500 000 | 5 311 000 000 | 12 930 000 000 | |
| 501 187 | 280 200 000 | 1 572 000 000 | 1 297 000 000 | 7 059 000 000 | 20 520 000 000 | |
| 630 957 | 404 900 000 | 3 181 000 000 | 2 061 000 000 | 17 570 000 000 | 32 570 000 000 | |
| 794 328 | 580 700 000 | 3 691 000 000 | 3 265 000 000 | 21 090 000 000 | 51 650 000 000 | |
| 1 000 000 | 846 100 000 | 4 724 000 000 | 5 182 000 000 | 28 310 000 000 | 82 000 000 000 | |
| 1 258 925 | 1 221 000 000 | 9 570 000 000 | 8 168 000 000 | 70 280 000 000 | 130 300 000 000 | |
| 1 584 893 | 1 750 000 000 | 11 050 000 000 | 12 970 000 000 | 84 120 000 000 | 207 300 000 000 | |
| 1 995 262 | 2 549 000 000 | 14 230 000 000 | 20 610 000 000 | 112 700 000 000 | 329 700 000 000 | |
| 2 511 886 | 3 676 000 000 | 28 800 000 000 | 32 610 000 000 | 279 900 000 000 | 525 100 000 000 | |
| 3 162 278 | 5 247 000 000 | 32 980 000 000 | 51 600 000 000 | 335 600 000 000 | ||
| 3 981 072 | 7 654 000 000 |
wszystkie czasy podane są w nanosekundach (NS), podane są 4 znaczące liczby. Wszystkie powyższe testy zostały przeprowadzone na Intel Core 2 Quad Q6600 (2.40 GHz) przy użyciu pojedynczego wątku, Windows XP SP 3, Java 1.6.0_22.
dowody
wykładnik macierzy
do udowodnienia tej tożsamości użyjemy słabej indukcji.
przypadek podstawowy
Dla \(n = 1\), wyraźnie \( \left^1 = \left \).
krok indukcyjny
załóżmy dla \(N ≥ 1\), że \( \left^n = \left \). Następnie:
\(\left^{N + 1} \ \ = \ left^n \left \ \ = \ left \ left \ \ = \ left \ \ = \ left.\)
szybkie podwajanie
Zakładamy, że metoda wykładnictwa macierzy jest poprawna dla wszystkich \(N ≥ 1\).
\(\left \\= \left^{2n} \\= \left( \left^n \right)^2 \\= \left^2 \\= \left.\)
zatem, porównując komórki w macierzy:
\(\begin{align}F(2n+1) &= F(n+1)^2 + F(n)^2. \\F(2n) &= F(n) \left \\&= F(n) \left \\&= F(n) \left. \\F(2n-1) &= F(n)^2 + F(n-1)^2.\end{align}\)