w dobie cyfrowego świata widzimy rekomendacje w każdej dziedzinie.jest to strona e-commerce, rozrywka czy serwisy społecznościowe. Rekomendacja nie tylko daje użytkownikowi zalecany wybór (na podstawie wcześniejszej aktywności), ale także opowiada o zachowaniu użytkownika (analiza sentymentalna lub AI emocji).

więc najpierw zrozummy, czym jest rekomendacja. Jest to zasadniczo polecanie elementu użytkownikowi na podstawie jego wcześniejszych poszukiwań / aktywności.

Rysunek 1 przedstawia rekomendację Amazon na podstawie historii przeglądania i przeszłych wyszukiwań. Możemy więc powiedzieć, że rekomendacja to zasadniczo przewidywanie przyszłych zachowań w oparciu o zachowania przeszłe. Istnieją dwa rodzaje podejść, które są stosowane w systemie rekomendacji

1 – filtrowanie oparte na treści

2 – filtrowanie oparte na współpracy

filtrowanie oparte na treści-

opiera się na idei polecania elementu użytkownikowi K, który jest podobny do poprzedniego elementu wysoko ocenianego przez K. podstawową koncepcją w filtrowaniu opartym na treści Jest TF-IDF (Term frequency — inverse document frequency), który jest używany do określenia znaczenia dokumentu/słowa/filmu itp. Filtrowanie oparte na treści pokazuje przejrzystość w zaleceniu, ale w przeciwieństwie do filtrowania opartego na współpracy nie może pracować wydajnie dla dużych danych

filtrowanie oparte na współpracy

opiera się na idei, że ludzie, którzy mają takie samo zainteresowanie pewnymi rodzajami elementów, będą również mieli takie samo zainteresowanie pewnymi rodzajami elementów, w przeciwieństwie do treści opartych na metadanych, które w zasadzie opierają się na metadanych, podczas gdy zajmują się rzeczywistą aktywnością. Ten typ filtrowania jest elastyczny dla większości domen (lub możemy powiedzieć, że jest to domena wolna), ale z powodu problemu zimnego startu, sparsity danych (który był obsługiwany przez faktoryzację macierzy) tego typu algorytm napotyka pewne niepowodzenie w pewnym scenariuszu.

Faktoryzacja matrycy

Faktoryzacja matrycy jest w centrum uwagi po konkursie Netflix (2006), kiedy Netflix ogłosił nagrodę pieniężną w wysokości 1 miliona dolarów dla tych, którzy poprawią średnią kwadratową wydajności o 10%. Netflix dostarczył zestaw danych szkoleniowych 100 480 507 ocen, które 480 189 użytkowników dało filmom 17 770.

Faktoryzacja macierzy jest metodą filtrowania opartego na współpracy, w której macierz m*n rozkłada się na m*k i k*N. Jest on zasadniczo używany do obliczania złożonych operacji macierzy. Podział macierzy jest taki, że jeśli pomnożymy macierz podzieloną otrzymamy macierz pierwotną, jak pokazano na rysunku 2. Jest on używany do wykrywania utajonych cech między dwoma jednostkami (może być użyty dla więcej niż dwóch jednostek, ale będzie to objęte faktoryzacją tensorową)

rozkład macierzy można podzielić na trzy typy-

rozkład 1 – LU — rozkład macierzy na macierze L I U, gdzie L jest macierzą trójkątną niższą, A U jest macierzą trójkątną górną, zwykle używaną do znajdowania współczynnika regresji liniowej. Rozkład ten nie powiódł się, jeśli macierz nie mogła się łatwo rozkładać

2 – QR rozkład macierzy – rozkład macierzy NA Q i R, gdzie Q jest macierzą kwadratową, A R jest macierzą trójkątną górną (nie jest to konieczne kwadratem). Używany do analizy układu eigen

rozkład 3 – Cholesky ’ ego – jest to najczęściej używany rozkład w uczeniu maszynowym. Stosowany do obliczania najmniejszego kwadratu liniowego regresji liniowej

Faktoryzacja macierzy może być stosowana w różnych dziedzinach, takich jak rozpoznawanie obrazów, rekomendacja. Matryce używane w tego typu problemach są na ogół rzadkie, ponieważ istnieje szansa, że jeden użytkownik może ocenić tylko niektóre filmy. Istnieją różne zastosowania do faktoryzacji macierzy, takie jak redukcja wymiarowości (aby dowiedzieć się więcej o redukcji wymiarowości, patrz przekleństwo wymiarowości), dekompozycja wartości utajonej

Oświadczenie o problemie

w tabeli 1 Mamy 5 użytkowników i 6 filmów, w których każdy użytkownik może ocenić dowolny film. Jak widać, Henry nie oceniał Thora, a Rocky podobnie Jerry nie oceniał Avatara. W realnym świecie te typy macierzy mogą być bardzo rzadkie

nasz problem polega na tym, że musimy znaleźć oceny dla filmów bez oceny, jak pokazano w tabeli 1

naszym celem jest znalezienie oceny użytkownika na podstawie faktoryzacji macierzy, ale wcześniej musimy przejść przez rozkład wartości pojedynczej (SVD), ponieważ Faktoryzacja macierzy i SVD są ze sobą powiązane

SVD i Faktoryzacja macierzy

przed przejściem do głębi SVD pozwala najpierw zrozumieć, czym jest K i transponować (K). Jeśli wykonamy PCA na macierzy K (Tabela 1) otrzymamy cały wektor użytkownika. Później możemy umieścić te wektory w kolumnie macierzy U i jeśli wykonamy PCA na transpozycji(K) otrzymamy cały wektor filmu, który staje się kolumną dla macierzy M.

więc zamiast wykonywać PCA na k i transpozycję(K) osobno, możemy użyć SVD, które może wykonać PCA Na K i transpozycję (K) w jednym ujęciu. SVD jest w zasadzie podzieloną macierzą K na macierz U, macierz M i macierz diagonalną:

gdzie k to macierz oryginalna, u to macierz użytkownika,m to macierz filmowa, a środkowa to macierz diagonalna

dla uproszczenia możemy na jakiś czas usunąć macierz diagonalną, więc nowe równanie staje się:

niech R jest klasyfikacją zdefiniowaną dla użytkownika u i elementu i, p jest wierszem M dla użytkownika, a q jest kolumną transpozycji(U) dla określonego elementu i. tak więc równanie stanie się:

uwaga — jeśli k jest gęstą wartością macierzy, to m będzie wektorem własnym k*transponowanym(K), podobnie wartość u będzie wektorem własnym transponowanym(K)*K, ale nasza macierz jest macierzą rzadką, nie możemy obliczyć U I m za pomocą tego podejścia

więc tutaj naszym zadaniem jest znalezienie macierzy m i U. Jednym ze sposobów jest zainicjalizowanie losowej wartości na M I U i porównanie jej z oryginalną Macierzą K, jeśli wartość jest bliska K, niż zatrzymanie procedury w przeciwnym razie zminimalizowanie wartości U I m, dopóki nie będą bliskie K. Proces tego typu optymalizacji nazywa się spadaniem gradientu

naszym podstawowym zadaniem jest zminimalizowanie funkcji średniego błędu kwadratowego, która może być reprezentowana jako :

As our main task is to minimize the error i.e. musimy znaleźć, w jakim kierunku powinniśmy iść, aby to zrobić, musimy odróżnić jego konsekwencji nowe równanie będzie

Dlatego, zaktualizowana wartość dla p i u będzie teraz:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Na podstawie tej linii decyzyjnej możemy rozróżnić dystrybucję danych

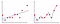
na rysunku 2 Pierwszy wykres to miejsce, w którym model jest dopasowany liniowo, podczas gdy na drugim wykresie jest on wyposażony w Stopień wielomianowy. Na pierwszy rzut oka wygląda na to, że drugi wykres jest znacznie lepszy niż pierwszy wykres, ponieważ daje 99% dokładności danych treningowych, ale co, jeśli wprowadzimy dane testowe i damy 50% dokładności danych testowych . Ten rodzaj problemu nazywa się overfitting i aby go przezwyciężyć, Wprowadzamy koncepcję zwaną regularyzacją.

jako problem przepełnienia jest powszechne w uczeniu maszynowym, więc istnieją dwa rodzaje podejścia regularyzacji, które mogą być wykorzystane do usunięcia przepełnienia

1 – L1 regularyzacja

2 – l2 regularyzacja

L1 regularyzacja dodać liniową wielkość współczynnika jako okres kary, podczas gdy w L2 dodać kwadratową wielkość współczynnika do funkcji straty/funkcji błędu (jak omówiono powyżej). L1 zwraca rzadkie macierze, podczas gdy L2 nie. Regularyzacja L1 sprawdza się dobrze w doborze funkcji w macierzy rzadkiej.

w zestawie danych rekomendacji również istnieją duże szanse na przepełnienie danych. Tak więc, aby usunąć problem nadmiaru możemy dodać regularyzację L2 (ponieważ macierz jest już rzadka, nie potrzebujemy tutaj regularyzacji L1) W funkcji strat stąd nowe równanie funkcji strat będzie:

ponownie możemy znaleźć gradient na zaktualizowanym MSE i uzyskać zaktualizowane punkty, stosując to samo podejście, co omówiono powyżej

jedną ważną rzeczą, którą należy wziąć pod uwagę w powyższym scenariuszu macierz P i q są nieujemne, dlatego te typy faktoryzacji są również nazywane nieujemną faktoryzacją. Ponieważ Faktoryzacja nieujemna automatycznie pobiera informacje o nieujemnym zbiorze wektora. NMF jest szeroko stosowany w przetwarzaniu obrazów, eksploracji tekstu, analizie danych o wysokich wymiarach